лекции / 1 Булевы функции

1 Булевы функции – это функции которые принимают только два знака 0 или 1 а х, х1, х2,…хn выступают в роли набора нулей и единиц, зависит от любого количества переменных, эту функцию можно задать таблицей истинности

2 Свойства булевых функций – 1)конъюнкция, дизъюнкция, сумма по модулю 2, стрелка Пирса, штрих Шэйфера – обладают свойством коммутативности

2) конъюнкция, дизъюнкция, сумма по модулю 2 обладают свойствами ассоциативности и дистрибутивности [а или (b или c) = (a или b) или с a или (b и c)=(a или b) и (a или c)]

3)Закон ДеМоргана [ не (a и b)= (не a) или (не b) не (a или b)=(не a) и (не b)]

4) Закон двойного отрицания [не(не a) = a]

5) выражение дизъюнкции через конъюнкцию и сумму по модулю 2[a или b= a и b +2 b +₂ a]

6) выражение дизъюнкции через импликацию [ a v b =(a->b)->b]

7)выражение отрицания через | , ↓, ↔, +₂ [не а =a|a, a ↓ a, a+₂1, a↔0]

8) выражение конъюнкции через | [a и b =(a|b)|(a|b)]

9) выражение дизъюнкции через ↓ [a v b=(a↓b) ↓(a↓b)

10)закон поглощения [a и b или a = a]

11) закон склеивания [не а или а = не а +₂а =1]

12) для функций конъюнкция, дизъюнкция, сумма по модулю 2 справедливы тождества

а и а = а Не а и а =0 а и 0 = 0 а и 1 = а

А или а =а Не а или а = 1 А или 0 = а А или 1 = 1

а+2 а = 0 а +2 не а = 1 а +2 0 = а а +2 1 = не а

3 Двойственность – Пусть функция f( x1, x2,…, xn) – булева функция, f*(x1, x2,…, xn) является двойственной если f*(x1, x2,…, xn) = f(не x1, не x2,…, не xn) функция называется самодвойственной если f*=f

4 Дизъюнктивные и конъюнктивные нормальные формы – конъюнктивным одночленом от переменных х1, х2,… хn называется конъюнкция этих переменных или их отрицаний

Аналогично для дизъюнктивного одночлена

5 СДНФ и СКНФ – СДНФ – это ДНФ , в которой каждый конъюнктивный одночлен, каждая переменная Xi из набора f’(x1, x2,…, xn) входит ровно 1 раз причём либо сама либо её отрицание

СКНФ – это КНФ которая удовлетворяет следующим условиям

1. КНФ не содержит 2-х одинаковых дизъюнкций

2. Ни одна из дизъюнкций не содержит одновременно некоторую переменную и её отрицание

3. Ни одна из дизъюнкций не содержит одновременно 2-х одинаковых переменных

4. Каждая дизъюнкция СКНФ содержит либо переменную либо её отрицание, для всех переменных входящих в формулу

6 Многочлен Жегалкина – называется многочлен являющийся суммой константы и различных одночленов в которые каждая переменная входит невыше чем в 1-ой степени. Многочлен Жегалкина константы равен самой константе

7 Логические исчисления - оперируют высказываниями. Высказывание – повествовательное предложение о котором в данной ситуации можно сказать, что оно истинно или ложно, но нито, ни другое одновременно

8 Логические отношения – иногда бывает желательно рассмотреть взаимоотношение 2-х высказываний. Наиболее интересное из таких соотношений имеет место когда из одного высказывания логически следует другое. Если X следует Y, то говорятч то Y является следствием Х. Отношение следствия можно охарактеризовать таким образом: из Х следует Y если Y истинно всякий раз, когда истинно Х, т.е. если y истинно во всех логических возможных случаях в которых Х истинно. В случае составных высказываний, имеющих одни и теже компоненты, таблицы истинности дают удобный метод для проверки того, имеют ли место соотношения следствия.2 высказывания называются не совместимыми, если из одного следует ложность другого

9 Варианты импликации

XY 00 01 10 11

НеX неY 11 10 01 00

X→Y 1 1 0 1

Y→X 1 0 1 1

Не X→не Y 1 0 1 1

Не Y→не X 1 1 0 1

10 Осн. законы определяющие свойства логич. операций

1. Х или Х ↔ Х, Х и Х ↔ Х

2. Коммутативность конъюнкции и дизъюнкции

3. Ассоциативность конъюнкции и дизъюнкции

4. Дистрибутивность операций конъюнкции и дизъюнкции

5. Двойное ортицание

6. Закон ДеМоргана

7. Склеивание

8. Поглощение

9. Действия с логическими константами

10. Закон исключения 3-го

11. Х↔Х

12. Отрицание противоречий

13. Контропозиция

14. Ценное заключение

15. Противоположность

16. (Х и(Х →Y))→Y↔1

11 Предикаты – функция значениями которой высказывания о «n»-обьектах представляющих значения аргументов

12 Кванторы – Квантор общности - это оператор, приводящийся в соответствие любому заданному предикату Y=P(x) такую двузначную логическую переменную Z, которая принимает значение 1 тогда и только тогда, когда Y=1 при всех значениях Х.

Квантор существования – это оператор приводящий в соответствие любому одноместному предикату Y=P(x) такую двузначную логическую переменную Z каторая принимает значение ) тогда и толь ко тогда, когда Y=0 при всех значениях Х

13 Действия над кванторами

1. Перенос квантора через отрицание

2. Вынос квантора за скобки

3. Перестановка одноимённых кванторов

4. Переименование связанных переменных

14 Уравнения математической физики. Уравнение колебания струны – под струной понимается тонкая нить, которая может свободно изгибаться. Если струну вывести из состояния равновесия а затем предоставить самой себе, то струна начнёт колебаться

15 Решение Даламбера – Рассмотрим случай свободных колебаний бесконечной струны. Искомая функцияU(x,t) должна удовлетворять уравнению (1)и начальным условиям U(x,0)=φ(x) (2) и 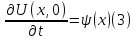. Так как струна неограниченна, то функции φ(х) и 𝜓(х) должны быть заданы в промежутке ( -∞; ∞) Найдём самое общее решение уравнения (1). Преобразуем уравнение (1) к новым независимым переменнымξ=x-at, η=x+at

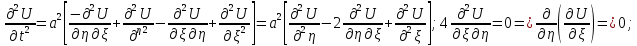
Частная по η=0 значит не зависит от η проинтегрируем последнее уравнение

это самое общее решение уравнения 1 оно называется решением Даламбера

16 Решение Фурье

17 Уравнение распространения тепла в стержне

18 Распространение тепла в пространстве – опытным путём установлено что количество тепла протекающего через площадку ΔS равно: ΔQ =-k(𝜕U/𝜕n)ΔS. Количество тепла протекающего через всю поверхность ΔQ*Δt=-k*gradU*n*ΔSΔt

19 Численное решение уравнения распространения тепла в стержне методом конечных разностей

Данная формула справедлива, если l≤ если шаг подобрать так чтобы скобка то формула примет вид:

20 Задача приводящая к исследованию уравнений Лапласа – формулировка краевых задач

1. Стационарное распределение температуры в однородном теле

1. Если известна температура поверхности тела т.е. U=φ(x), То такая задача называется задачей диракля или первой краевой

2. Если известен тепловой поток в каждой точке поверхности, который пропорционален

то задача называется второй краевой или задачей Кеймана.

2. Потенциальное течение жидкости или газа

Теория функции комплексной переменной

22 Комплексные числа. Алгебраическая и тригонометрическая форма записи. Действия над комплексными числами - комплексным числом называется выражение вида z=x+iy(алгебраическая форма записи), где i мнимая единица.

1. Сложение и вычитание

2. Умножение

3. Деление

Cosnφ+icosnφ – тригонометрическая форма записи

23 Элементарные функции комплексной переменной – элементарной функцией комплексной переменной называют функции, которые получаются из элементарных функций вещественной переменной, определяемых разложением в степенной ряд по следующему правилу, если z=t(x)=a0+a1x+…+anxⁿ+… - элементарная функция вещественной переменной х, то w=f(z)=a9+a1z+…+anzⁿ+… - элементарная функция комплексной переменной z очевидно, что функция определяется лишь для таких значений комплексной переменной при которой ряд сходится.

1. Степенная функция W= Zⁿ Степенная функция определена для всех комплексных чисел. Каждому комплексному числу она ставит соответствие Zⁿ т.е. произведение n-множителей каждый из которых равен n. Данная функция обладает свойствами вещественного переменного

2. Показательная функция

24 Производная функции комплексной переменной Условие Коши-Мимона

25 Геометрический смысл производной функции комплексного переменного

26 Интегрирование по комплексному аргументу

27 Свойства криволинейного интеграла. Теорема Коши. Формула Ньютона – Лейбница

28 Формула Коши (2 следствия)

29 Степенные ряды с комплексными числами

30 Изолированные особые точки и их классификация

31 Ряд Лорана. Вычиты

32 Операционные исчисления. Преобразования Лапласа

33 Свойства преобразований Лапласа

34 Свёртка функций. Теорема об умножении изображения. Интеграл Дюамеля

35 Таблица некоторых преобразований Лапласа

36 Формула обращения

37 Оригиналы с рациональными изображениями

38 Теория вероятности. Классическое определение вероятности. Свойства вероятности

39 Основные свойства комбинаторики

40 относительная частота

41 Теоретические вероятности

42 Теорема сложения вероятностей

43 Теорема умножения вероятностей

44 Независимые события

45 Теорема сложения вероятностей совместных событий

46 Формула полной вероятности

47 Вероятность гипотез

48 Формула Бернулли

49 Локальная теорема Лапласа

50 Интегральная теорема Лапласа

51 Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях

52 Случайные величины, дискретные и непрерывные случайные величины

53 Закон распределения вероятности дискретной случайной величины

54 Биномиальное распределение

55 Числовые характеристики случайной величины. Математической ожидания, его свойства

56 Дисперсия случайной дискретной величины

57 Среднеквадратичное отклонение суммы независимых случайных величин

58 Одинаково распределённые независимые случайные величины

59 закон больших чисел

60 функция распределения вероятностей случайной величины

61 Плотность распределения вероятности случайной величины

62 Числовые характеристики непрерывных случайных величин

63 Равномерное распределение

64 Показательное распределение

65 Нормальное распределение

66 Вероятность попадания в интервал нормальной случайной величины

67 вычисление вероятности заданного отклонения для нормально распределённой случайной величины

68 Задача математической статистики

69 Генеральная и выборочная совокупность

70 Способы отбора

71 Статистическое распределение выборки

72 Эмпирическая функция распределения

73 Полином и гистограмма

74 Статистическая оценка параметров распределения

75 Генеральная и выборочная средняя. Оценка генеральной средней по выборочной средней

76 Групповая и общая средняя

77 Генеральная дисперсия, выборочная дисперсия

78 оценка генеральной дисперсии по исправленной выборочной

79 Точность и надёжность оценки. Доверительный интеграл

80 Доверительный интервал для оценки математического ожидания нормального распределения при известном δ

81 Оценка биноминального распределения по относительной частоте

82 интервальная оценка

83 Эмпирические моменты

84 Метод моментов для точной оценки параметров распределения