1.Метод еквівалентної заміни

При розрахунку БГАЛС використовують заміну вузлів еквівалентними елементами. Розглянемо можливі варіанти заміни вузла. Так КС є вузловою для 1 – го вузла (рис.1, лекц. 4) і вхідною для 4-ї вітки. Частину БГАЛС пристиковану до повної 4-ї вітки можна замінити еквівалентним елементом без вузлової КС, який характеризується коефіцієнтом готовності до видача касет (рис.1):

(5.1)

де , - коефіцієнти готовності до видачі касет основних 1-ї і 2-ї вхідних віток.

Частину БГАЛС пристиковану до виходу 1-го вузла (вузлової КС), можна замінити еквівалентним елементом (рис.4)_. - це коефіцієнт готовності до прийому касет по основному входу 4-ї вітки, визначається згідно ф-ли (4.8, лекц.4) :

(5.2)

де , - коефіцієнти готовності 4-ї і 5-ї основної віток до прийому касет, - коефіцієнт готовності 3 – ї спряженої вітки до видача касет.

Час обслуговування касет на вхідних чи вихідних КС до яких пристиковані еквівалентні елементи вибирається максимальним з часів обслуговування на КС в приєднаних елементах, в тому числі самих вхідних чи вихідних КС.

Попередні вузли можна пристиковувати як до повних входів (рис.1), так і до основних входів наступних вузлів (рис.3). В цьому випадку перший вузол заміняється еквівалентним елементом , який включає в себе вузлову КС :

(5.3)

де , - коефіцієнти готовності 1-ї і 2-ї спряжених вхідних віток до видачі касет, - коефіцієнти готовності КС.

Якщо проводити розрахунок відносно повної проміжної вітки (рис.4), в яку входять вузлові КС і КС , то до неї необхідно приєднати еквівалентні елементи - готовність попереднього вузла без КС видавати касети і еквівалентний елемент коефіцієнт готовності вузла після КС до прийому касет.

(5.4)

де - коефіцієнт готовності спряженої 3-ї вітки до видачі касет,- коефіцієнт готовності основної 5-ї вітки до прийому касет.

У випадку коли між двома сусідніми накопичувачами не одна, а кілька КС, всі ці КС можна замінити узагальненою КС. Граф станів ділянки з кількох послідовно з’єднаних КС зображено на рис.5. Ймовірні стани ділянки S₀ – ділянка справна, S₁-S_n – відмовні стани, коли одна з КС несправна. Приймається що дві КС одночасно вийти з ладу не можуть.

Граф узагальненої КС приведено на рис.6. Узагальнена КС має два стани S₀ – справна, S- несправна.

При заміні ділянки послідовно з’єднаних КС узагальненою визначають інтенсивність потоку відмов і відновлень узагальненої КС. Час обслуговування касети узагальненою КС визначають максимальним із часів обслуговування на КС, яка входить в узагальнену КС(мінімальна продуктивність).

Інтенсивність потоку відмов узагальненої КС:

. (5.5)

Коефіцієнт готовності (ймовірність безвідмовної роботи) узагальненої КС:

. (5.6)

Інтенсивність потоку відновлень узагальненої КС :

. (5.7)

Описаний вище метод розрахунку БГАЛС базується на заміні вузлів і віток еквівалентними елементами.

2. Метод послідовної згортки

Розглянемо метод розрахунку БГАЛС шляхом послідовної згортки. Вирази приводяться для основної ділянки вітки, оскільки для спряженої вони аналогічні. Припускається, що ділянка має два факторних стани: Sк₀ – робочий і Sк₁ – неробочий. З стану Sк₀ в Sк₁ ділянку переводить сумарна інтенсивність потоку відмов і навпаки, З стану Sк₁ в Sк₀ ділянку переводить сумарна інтенсивність потоку відновлень .

Згідно формул для визначення ймовірності перебування ділянки в робочому стані (лекція 1), коефіцієнт готовності к-ї ділянки до прийому касет:

(5.8)

З стану Sк₀ в Sк₁ ділянку переводять потоки з інтенсивностями , (див граф станів, лекц. 3), причому - з положення, в якому ділянка знаходиться з ймовірністю , а з положення в якому ділянка знаходиться з ймовірністю . Тоді:

. (5.9)

Оскільки

, (5.10)

то . (5.11)

Якщо в формулу (5.9) підставити формули для визначення ймовірності перебування ділянки в робочому стані і (лекц.3), отримаємо:

. (5.12)

Якщо в формулу (5.11) підставити формули (5.8) і (5.10) , отримаємо:

. (5.13)

Таким чином к-й основна (спряжена) ділянка представляється одним узагальненим елементом(КС) з двома станами – справний-несправний. Цей узагальнений елемент об’єднується з попередньою (наступною) КС, використовуючи формули (5.5 - 5.7). В результаті отримується узагальнена КС, яка в свою чергу об’єднується з попереднім(наступним для спряженої ділянки) накопичувачем. Таким чином відбувається послідовна згортка лінії.

Слід зауважити, що згортки по основним ділянкам проводиться з кінця вітки, о по спряженим – з початку(рис.7).

Лекція 6. Ймовірність працездатності системи з 2-х станів

Якщо в системі діють Пуасоновські потоки відмов і час відновлення розподілений по експоненціальному закону, функція готовності визначається з використанням системи диференціальних рівнянь ймовірностей станів:

(6.1)

де n – число станів в яких може перебувати система в результаті дії потоків випадкових подій, і - інтенсивності потоків, які переводять систему з деякого стану в і навпаки.

Розглянемо об’єкт(наприклад КС), який має два стани: працездатний - S₀ i відмовний - S₁.

Систему диференціальних рівнянь зручно складати на основі розміченого графа (рис.6.1):

Початкова умова:

=1, =0. (6.4)

Це лінійна система диференціальних рівнянь першого порядку. Його можна розв’язати методом виключення. Для цього продиференціюємо рівність (6.2):

. (6.5)

Підставимо (6.3) в (6.5):

, (6.6)

з рівності (6.2) отримаємо:

. (6.7)

Враховуючи в рівності (6.5) рівність (6.7) отримаємо лінійне однорідне диференціальне рівняння другого порядку:

, (6.8)

з якого, враховуючи що , , , одержуємо характеристичне рівняння:

, або (6.9)

корені рівняння =0 і =-() – дійсні і різні, в цьому випадку частинними розв’язками будуть , і, відповідно:

. (6.10)

Підставивши (6.10) в (6.7) отримаємо:

(6.11)

(6.12)

Задовольняємо початкові умови:

, (6.13)

звідси

, , ,

тоді

, , (6.14)

враховуючи (6.14) в (6.12) отримуємо:

(6.15)

Видно, що .

Якщо режим роботи системи усталений, тобто , отримаємо:

(6.16).

Лекція 7. Ймовірність працездатності системи з 4-х станів при

усталеному режимі роботи

Розглянемо об’єкт (основну ділянку ГАЛС), який має чотири стани S₀ , S₁ , S₂, S₃ (рис.7.1). Суть кожного з станів описано в (лекц.3). Користуючись системою диференціальних рівнянь ймовірностей станів, яка у загальному випадку записана в вигляді:

, (7.1)

а також розміченого графа (рис.7.1), складемо систему диференціальних рівнянь для заданого об’єкта:

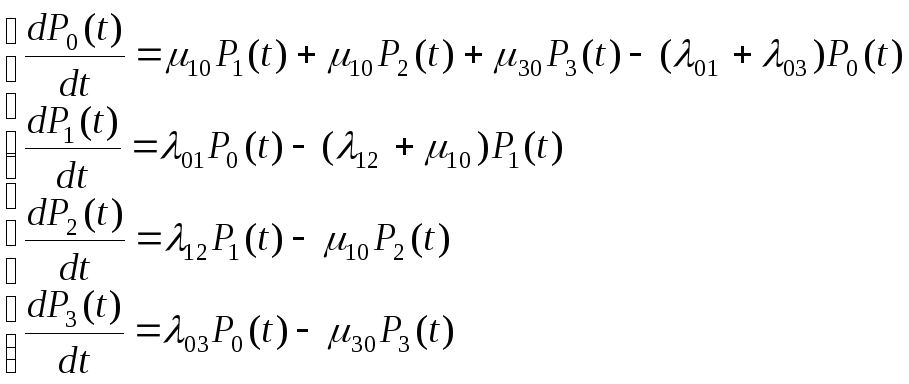(7.2)

Це лінійна система диференціальних рівнянь відносно функцій .

Початкові умови, при t=0:

=1, =0, =0, =0. (7.3)

Згідно початкових умов, при t=0, тобто при запуску ГАЛС система перебуває в повністю справному стані, якому на графі(рис.7.1) відповідає стан S₀.

Нормувальна умова :

, (7.4)

тобто перебування системи в одному з чотирьох станів є достовірною подією.

Розглянемо суть побудови системи диференціальних рівнянь на прикладі побудови диференціального рівняння, яке визначає ймовірність перебування системи в стані S₀ (перше рівняння системи(7.2)). Перший доданок рівності (7.1) є сумою добутків ймовірностей перебування системи в станах S₁ , S₂, S₃ на інтенсивності потоків , які переводять систему в стан . В даному випадку(рис.7.1), це інтенсивності потоків відновлення . Другий доданок (з знаком “-“) рівності (7.1) є добутком ймовірності перебування системи в стані S₀ на суму на інтенсивностей потоків , які переводять систему зі стану S₀ в інші стани. На рис.7.1 це інтенсивності потоків відмов і . Таким чином , використовуючи узагальнену систему рівнянь (7.1) і розмічений граф станів (рис. 7.1) отримується система диференціальних рівнянь (7.2).

Розглянемо випадок усталеного режиму роботи системи, тобто коли . В цьому випадку ймовірності перебування системи в будь-якому стані є сталими:

(7.5)

У цьому випадку, ввівши позначення: ; ; ; і зважаючи на те, що похідні від сталих рівні нулю із системи (7.2) отримаємо систему лінійних однорідних алгебраїчних рівнянь відносно :

. (7.6)

Знайдемо основний визначник системи, розклавши його на елементи 4-го стовпця:

=0.

Якщо основний визначник системи рівний нулю, то система лінійних однорідних алгебраїчних рівнянь має ненульові розв’язки. Видно, що відмінний від нуля базисний мінор утворюють коефіцієнти при А₀, А₁, А₂ . Тому можна прийняти А₃ =С, де С – деяка стала. Із системи (7.6) отримаємо:

, (7.7)

, (7.8)

, (7.9)

з урахуванням умови (7.4) отримаємо:

. (7.10)

Після простих математичних перетворень отримаємо:

; (7.11)

; (7.12)

; (7.13)

. (7.14)

Оскільки система вважається працездатною коли перебуває в стані S₀ або S₁, то ймовірність її безвідмовної роботи, або коефіцієнт готовності визначається за формулою:

. (7.15)

Лекція 8. Ймовірність працездатності системи з 4-х станів при