(16)Автоматы Мура и Мили, основные понятия

Эквивалентность автоматов Мили и Мура. Введены две модели автоматов: автомат Мура и автомат Мили. Ниже следующая теорема показывает, что эти 2 модели равномощны, т.е. любой автомат можно реализовать в каждой из этих моделей. Теорема - для любого автомата Мура существует эквивалентный автомат Мили и наоборот. Доказательство теоремы построим на преобразовании автомата обного типа в автомпт другого типа, на примере конкретных автоматов, описанных с помощью графов.

Необходимость:  Докажем, что для любого(полностью определенного) автомата Мура существует эквивалентный ему автомат Мили.

                    Рассмотрим автомат Мура:

                    Sµ=<X,Y,A,d, m ,a§A>, где

               А={a1,a2,a3,a4};

X={x1,x2,x3};

Y={y1,y2};

описанный в виде графа

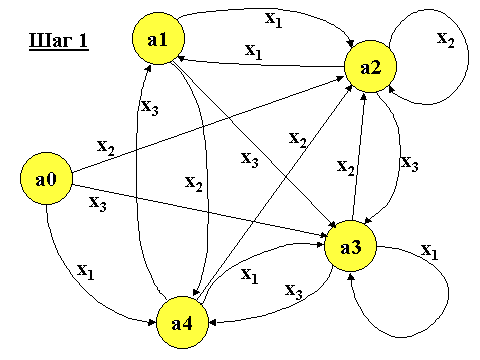
Перенесем выходы автомата с вершин графа на входящие ветви графа.

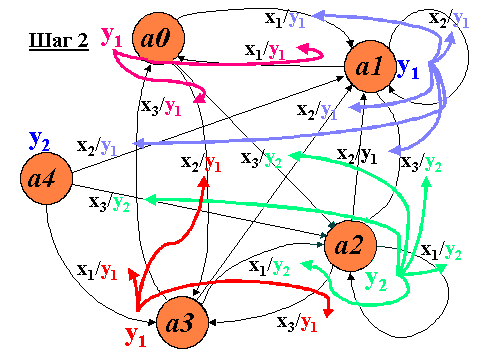
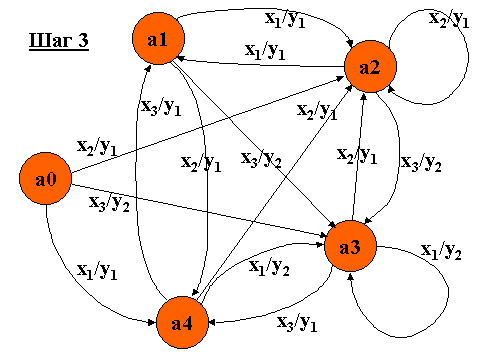
Получаем граф, который описывает автомат

                S'=<X',Y',A',d',l ,a§A'>, где

                A'=А={a0,a1,a2,a3,a4};

X'=X={x1,x2,x3};

Y'=Y={y1,y2};

       Автомат S'  эквивалентен автомату S, т.к для любого состояния a1§ A aавтомата S существует состояние    a1§ A' автомата S' такое, что реакции автоматов на любые слова в этих состояниях одинаковы, и наоборот.

Достаточность:

Докажем, что для любого полностью определенного автомата Мили существует эквивалентный ему автомат Мура.

Рассмотрим автомат Мили

                S=<X,Y,A,d,l ,a0§A'>, где

              А={a0,a1,a2,a3};

X={x1,x2};

Y={y1,y2,y3};

описанный в виде графа

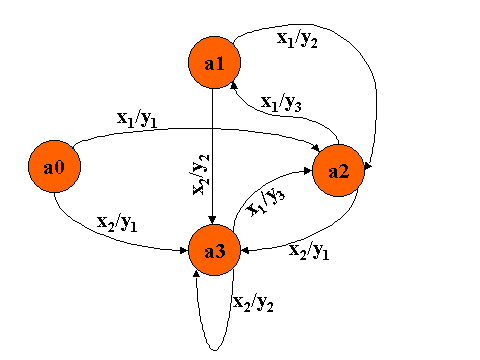
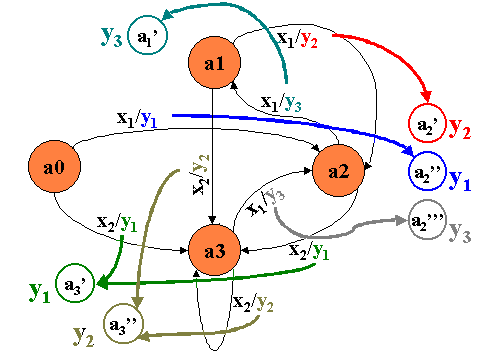
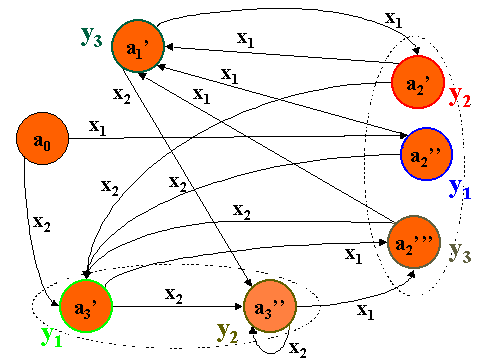
Таким образом получим граф, который описывает автомат

           S=<X',Y',A',d,m ,a0§A'>, где

            A'=А={a0,a1',a2',a2'',a2''',a3',a3''};

    X'=X={x1,x2};

    Y'=Y={y1,y2,y3};

Докажем, что автоматы S и S' эквивалентны. Для этого докажем, что для любого состояния ai§A автомата S существует эквивалентное ему состояние ai§A' автомата S' и наоборот.

Покажем, что для любого состояния множества {a0,a1,a2,a3} существует эквивалентное из множества  {a0,a1',a2',a2'',a2''',a3',a3''};

        a0~a0'       

        a1~a'1

        a2~a'2

        a3~a'3

покажем обратное утверждение

a0~a0          a'1~a1        a'2~a2        a'3~a3           

                                                 a''2~a2        a''3~a3

                                               a'''2~a2

(17)Триггеры, их виды и классификация

Триггер (англ. trigger), спусковое устройство, которое может сколь угодно долго находиться в одном из двух состояний устойчивого равновесия и скачкообразно переключаться из одного состояния в другое под действием внешнего сигнала. Триггер имеет два выхода: основной и инверсный. Каждому состоянию Триггеру соответствуют определённые сигналы на его выходах, отличающиеся своим уровнем. В одном состоянии на основном выходе Триггера формируется сигнал высокого уровня, а на инверсном — низкого; в др. состоянии, наоборот, сигналы высокого и низкого уровней формируются соответственно на инверсном и основном выходах. Триггер характеризуется следующими важнейшими параметрами: быстродействием, временем срабатывания, уровнями входных и выходных сигналов. Быстродействие Триггера определяется как максимальное возможное число переключений в единицу времени. Время срабатывания определяется временем перехода Триггера из одного состояния в другое и характеризует задержку выходного сигнала Триггера относительно входного. Под уровнем входного сигнала понимают минимальное значение сигнала, необходимое для переключения Триггера. Уровень выходного сигнала у большинства Триггеров не ниже уровня входного сигнала, чем обеспечивается возможность их последовательного соединения без промежуточного усиления. Наибольшее распространение получили электронные Триггеры, выполненные на электронных лампах, газоразрядных приборах, полупроводниковых диодах, транзисторах разных типов и особенно на интегральных микросхемах; иногда применяются также Триггеры на магнитных элементах, элементах пневмо- и гидроавтоматики и др. По характеру входных сигналов различают Триггеры с потенциальными входами (прямым и инверсным) и динамическими входами (также прямым и инверсным). Триггеры с потенциальными входами реагируют на сигнал высокого уровня на прямом входе и низкого уровня на инверсном входе. Триггеры с динамическими входами реагируют на перепады (изменения уровня) входных сигналов: положительный на прямом входе и отрицательный на инверсном. Наиболее часто применяют: Триггеры со счётным входом (Т-триггер), который изменяет своё состояние на противоположное с каждым входным сигналом; Триггер с двумя установочными входами (R — S-триггер), изменяющий своё состояние только при воздействии управляющего сигнала на определённый вход (R-или S-вход), причём повторное воздействие сигнала на тот же вход Триггер не изменяет его состояния; универсальный Триггер (J — K-триггер), обладающий свойствами Т-триггера и R — S-триггера; Триггер задержки (D-триггер), состояние которого и соответствующий ему выходной сигнал повторяют входной сигнал. Кроме Триггеров этих типов, применяют комбинированные Триггеры, представляющие собой универсальные многофункциональные устройства с большим числом входов. Указанные выше Т. относят к симметричным; применяют также несимметричные Т. (Т. Шмитта). Несимметричный Т. переходит из одного состояния в другое по достижении входным сигналом одного уровня (порога срабатывания), а в исходное состояние возвращается при уменьшении входного сигнала до некоторого др. уровня. Существуют и многостабильные Т., обладающие числом устойчивых состояний, большим, чем два. Т. различных типов применяют в устройствах цифровой вычислительной техники и автоматики. С использованием Т. строятся цифровые автоматы с программным управлением для дискретной обработки информации (в частности, счётчики, пересчётные устройства, регистры разных типов, дешифраторы, сумматоры и др.), формирователи импульсов, цифровые делители частоты и т.д. В цифровой автоматике Т. выполняют функции элементарных автоматов с памятью, имеющих 2 состояния, которым соответствуют два возможных значения двоичной логической переменной (х = 0 и х = 1). Такие Т. подразделяются на асинхронные и синхронные. Синхронные (тактируемые) Т. выполняют свои функции только при воздействии на их входы периодических тактовых сигналов (обычно меандрового типа), синхронизирующих работу Т. Синхронные Т. подразделяются на однотактные и двухтактные. Последние представляют собой систему из двух Т., выполняющих одну и ту же логическую операцию, но со сдвигом во времени на длительность полутакта входного тактового сигнала. Удвоение действий Т. необходимо для разделения во времени приёма информации, доставляемой входными сигналами, и передачи информации с выходов Т. на др. элементы устройства (или на его вход).