3.9.Метод Хемминга.
Выполнить прием Х18=1100 и проверку данных.
Определить и исправить ошибку в Х18=1100.
Выполнить повторное кодирование данных Х18=1100 и передачу по линии связи.
Выполнить прием Х18=1100 и проверку данных.
Кодирование данных и передача по линии связи :
а)Вычисление для данного D3D2D1D0 =1100 поверочных битов Р2Р1Р0 по формулам:
Р0 = D2 D1 D0 = 1 0 0 = 1;
Р1 = D3 D1 D0 = 1 0 0 = 1;
Р2 = D3 D2 D0 = 1 1 0 = 0.
Поверочные биты Р2Р1Р0 равны 011.
б) Передача сообщения D3D2D1D0Р2Р1Р0 = 1100 011
.
Прием и проверка данных:
а)Прием сообщения D3D2D1D0Р2Р1Р0 = 1100 011.
б)Вычисление
синдромов
:
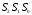S0 = D2 D1 D0 Р0 = 1 0 0 1 = 0;
S1 = D3 D1 D0 Р1 = 1 0 0 1 = 0;
S2 = D3 D2 D0 Р2 = 1 1 0 0 = 0.
Синдромы
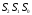равны 000.
в)Проверка на наличие ошибок:
-
из таблицы идентификаторов получаем,
что для синдромов
= 0000 ошибки нет.
Прием и проверка данных с ошибкой в 0 бите:
а)Прием сообщения D3D2D1D0Р2Р1Р0 = 1101 011.
б) Анализ принятого сообщения:
|
Данное |
Код Хемминга |
|||||
|
D3 |
D2 |
D1 |
D0 |
Р2 |
Р1 |
Р0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
в)Вычисление
синдромов
:
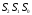S0 = D2 D1 D0 Р0 = 1 0 1 1 = 1 0 = 1;
S1 = D3 D1 D0 Р1 = 1 1 0 1 = 0 1 = 1;
S2 = D3 D2 D0 Р2 = 1 1 1 0 = 0 1 = 1.
г)Проверка на наличие ошибок:
-
для синдромов
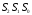= 101 из таблицы синдромов извлекаем
сообщение: «Ошибка в D0».
д) Исправление ошибки:
-
исправление ошибки с помощью логической
операции инверсии
(второго разряда)
=
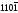1100.
Ответ. Передавалось данное 1100.
3.10.Метод crc (двоичное кодирование) :
Исходный двоичный код Х19=1101 0010, порождающий двоичный код X20=1011, множитель
двоичный X21=1000:
Выполнить кодирование данных Х19=1101 0010 и передачу по линии связи.
-
Выполнить прием и проверку данных.
Выполнить кодирование данных Х19=1101 0010 и передачу по линии связи (с ошибкой в бите X23=0)
Кодирование данных и передача по линии связи.
-Исходный
полином
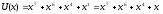=1101
0010
-Порождающий
полином
=
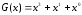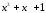= 1011
-Множитель
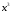= 1000
а)
Умножение исходного полинома
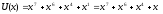=1101
0010
на
фиксированное двоичное число
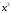= 1000:
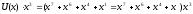=(1101
0010)1000=0110 1001 0000
|
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
= |
|
|
|
|
|
|
|
|
|
|
|
б)
Деление
полинома
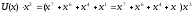=0110
1001 0000 на порождающий
полином
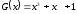= 1011:
Остаток
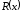= 0.
в) Формирование сообщения:
=
.
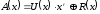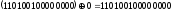г) Передача сообщения 1101 001 0000 0000
Прием и проверка данных.
а) Прием сообщения 0110 1001 0000 0000.
б)
Деление
сообщения
0110 1001 0000 0000 на
порождающий
полином
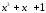= 1011:
|
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
= |
|
|
|
|
|
|
|
|
|
|
|
в)Проверка на наличие ошибок:
-
остаток
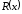равен нулю, ошибки нет.
Прием и проверка данных с ошибкой в 0 бите.
а) Прием сообщения 0110 1001 1000 0000.
б)
Деление
сообщения
0110 1001 1000 0000 на
порождающий
полином
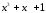= 1011:
|
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0
|
= |
|
|
|
|
|
|
|
в)Проверка на наличие ошибок:
-
остаток
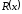не равен нулю, ошибка есть.