4.Скалярное, векторное и смешанное произведение векторов
Скалярное произведение векторов.
Определение. Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними.
Обозначение:
.
Теорема. (Свойства скалярного произведения.)
1). Скалярное произведение подчиняется закону коммутативности:
,
.
2). Скалярное произведение двух векторов равно нулю тогда и только тогда, когда хотя бы один из векторов нулевой или векторы ортогональны:
или
или
.
3). Скалярный квадрат вектора равен квадрату его модуля:
.
4).
.
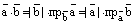Теорема. (Свойство линейности скалярного произведения.)
1) Скалярное произведение дистрибутивно относительно сложения векторов:
,
.
2) Скалярный множитель можно выносить за знак скалярного произведения:
,
,
Теорема. (Скалярное произведение векторов в координатной форме.) Скалярное произведение векторов равно сумме произведений соответствующих координат.
Другими словами,
пусть
,
.
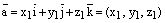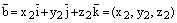Тогда
.
Следствие
1. Пусть
.
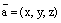Тогда
.
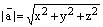Следствие 2. Пусть
,
.
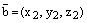Тогда
.
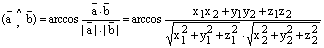Векторное произведение векторов.
Определение.
Векторным произведением вектора
на
вектор
называется
третий вектор
,
который удовлетворяет следующим трем
условиям:
1)
и
;
2)
тройка векторов
является
правоориентированной;
3)
.
Из
определения
следует, что, если векторы
,
и
отложить
от одной точки, то
1)
вектор
перпендикулярен
плоскости, в которой лежат векторы
и
2)
кратчайший поворот вектора
к
вектору
происходит
против часовой стрелки, если смотреть
"сверху", т.е. со стороны вектора
;
3) длина
вектора
численно
равна площади параллелограмма,
построенного на векторах
и
,
как на его сторонах.
Теорема. (Свойства векторного произведения.)
1). Антикоммутативность:
,
.
2). Условие коллинеарности векторов:
.
3).
Модуль
векторного
произведения численно равен площади
параллелограмма, построенного на
векторах
и
,
как на его сторонах.
Сме́шанное
произведе́ние
векторов
—
скалярное
произведение вектора
на
векторное
произведение векторов
и
:
.
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрический
смысл:
Модуль смешанного произведения численно
равен объёму параллелепипеда,
образованного векторами
.
Свойства
-
Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
-
Смешанное произведение
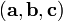в
правой декартовой системе координат
(в ортонормированном базисе) равно
определителю
матрицы,
составленной из векторов
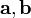и
:
-
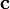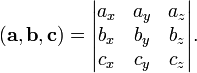
Смешанное произведение
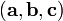в
левой декартовой системе координат (в
ортонормированном базисе) равно
определителю
матрицы,
составленной из векторов
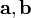и
,
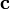взятому со знаком "минус":
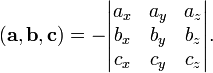
В частности,
-
Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.
-
Геометрический смысл — Смешанное произведение
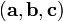по
абсолютному значению равно объёму
параллелепипеда,
-
образованного векторами
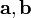и
;
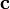знак зависит от того, является ли эта
тройка векторов правой или левой.