Глава ііі. Приклади розв’язання задач

Задача 3.1. Тонке однорідне півкільце радіуса r має масу m. Знайти силу притягання між цим півкільцем та тілом масою m_o, яка знаходиться в центрі кривизни півкільця та напруженість гравітаційного поля в центрі кривизни півкільця.

Р озв’язання задачі

Виділимо на півкільці (рис. 3.1.1) елемент довжини . Маса такого елемента, враховуючи, що півкільце однорідне, буде дорівнювати

.

Тоді за законом всесвітнього тяжіння сила притягання:

.

Розкладемо силу на дві складові та . Візьмемо симетрично елемент елементу (рис. 3.1.1), тоді сили в сумі дають нуль, а сили співпадають за напрямком і векторну суму цих сил можна замінити алгебраїчною сумою.

О чевидно

.

Із рис.3.1.2 видно, що , тоді

.

Напруженість гравітаційного поля визначається за формулою:

або .

Відповідь: ; .

Задача 3.2. Яку частку енергії випромінює земна куля, яку вона отримує від Сонця за 1 с, якщо температура поверхні Землі 0^о С і коефіцієнт поглинання дорівнює 1? Сонячна стала дорівнює С=1,3 кДж/м²·с.

Р озв’язання задачі

Сонячна стала – це енергія, яку приносять сонячні промені за 1 с на площу 1 м², що знаходиться поза атмосферою Землі, перпендикулярно до сонячних променів на середній відстані Землі від Сонця.

Тоді, енергія, яку поглинає Земля за одну секунду дорівнює добутку сонячної сталої на площу (R – радіус Землі) великого кола сфери Землі (рис. 3.2.1).

Тоді поглинута енергія рівна:

.

Енергію, яку випромінює Земля за цей період можна визначити таким чином:

.

Згідно з законом Стефана – Больцмана:

, де .

Врахувавши, що t=1 с, знайдемо відношення Е_випр до Е_пог:

.

Після розрахунків маємо: n=0,9.

Відповідь: n=0,9

Задача 3.3. Визначити, яка кількість ядер в 1 мг ізотопу церію розпадається за час:1) Δt₁=1с; 2) Δt₂=1рік? Період напіврозпаду церію Т=285 діб.

Розв’язання задачі

1. Процес радіоактивного розпаду носить статистичний характер. Тому при Δt₁<<Т можна вважати, що число ядер, які не розпалися, залишається практично постійним і рівним початковому числу ядер N₀. Для знаходження числа ядер, які розпалися ΔN запишемо закон радіоактивного розпаду у такому вигляді:

.

Стала радіоактивного розпаду пов’язана з періодом напіврозпаду таким чином:

.

Тоді маємо:

.

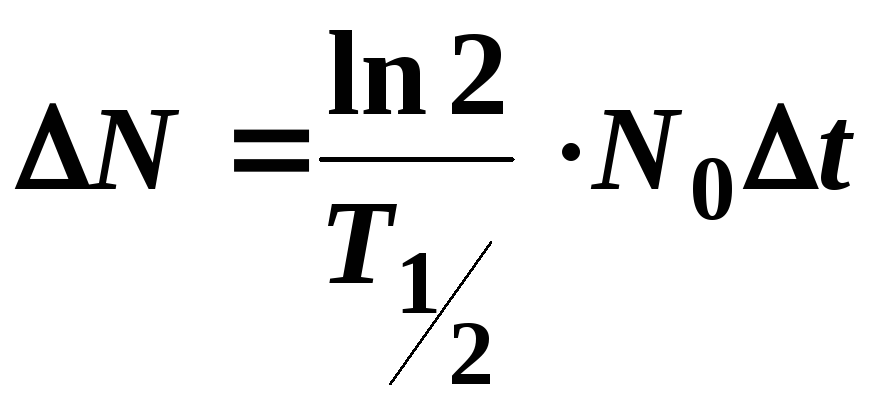Число атомів N₀ у m₀=1 г церію знайдемо зі співвідношення:

,

де N_А – число Авогадро; μ – молярна маса атома .

Врахувавши формулу для N₀, одержимо:

.

Після розрахунків маємо: ΔN₁=1,2·10¹¹атомів.

2. При Δt₁≈Т маємо можливість використати закон радіоактивного розпаду у такому вигляді:

.

Виражаючи

, та ,

маємо:

.

Після розрахунків маємо: ΔN₂=2,5·10¹⁸атомів.

Відповідь: ΔN₁=1,2·10¹¹, ΔN₂=2,5·10¹⁸.

Задача 3.4. Знайти коефіцієнт дисоціації водного розчину калію (КСl) з концентрацією С=0,1 г/см³. Питомий опір такого розчину ρ=7,4·10^-2 Ом·м при 18 ^оС, рухомість іонів К⁺ та при цій температурі рівні відповідно U₊=6,7·10^-8 м²/В·с та U_=6,8·10^-8 м²/В·с.

Розв’язання задачі

Коефіцієнт дисоціації можна визначити з формули залежності електропровідності від рухомості іонів:

,

де - та .

Оскільки, іони К⁺ та Сl^- є одновалентними, то заряд іона дорівнює заряду електрона: q=е.

Знайдемо невідому концентрацію розчину

,

де N – загальне число пар іонів, V – об’єм.

З другого боку, концентрація розчину ,

тоді

.

Число N можна виразити зі співвідношення

,

де N_А – число Авогадро; μ – молярна маса КСl, μ=74·10^-3 кг/моль.

Тоді

.

Отже

.

Остаточно маємо:

.

Після розрахунків маємо: α=0,8.

Відповідь: α=0,8.

Задача 3.5. На площі 400 км² за 10 хв випало 20 мм води у вигляді дощу. Підрахувати енергію та потужність тепловиділення від злиття крапель під час дощу, якщо краплі мають середній діаметр 3 мм поблизу Землі та утворюються з більш малих крапель діаметром 3·10^-3 мм.