
- •21. Функции. Понятие. Классификация.
- •22. Предел последовательности и его свойства.
- •23. Неопределенный интеграл и его свойства.
- •24. Определенный интеграл и его свойства.
- •25. Случайные события. Действия. Свойства.
- •26. Случайные события. Операции. (Теоретико-множественная трактовка).
- •27. Относительная частота. Свойства. Статистическое и классическое определение вероятности.
- •28. Элементы комбинаторики. Схема выбора без возвращения.
- •Число различных размещений из n элементов по m элементов определяется с помощью формулы
- •29. Элементы комбинаторики. Схема выбора с возвращением.
- •30. Геометрическое определение вероятности. Аксиоматическое определение вероятности.
30. Геометрическое определение вероятности. Аксиоматическое определение вероятности.
Геометрическое определение вероятности применяется, если исходы опыта равновозможны, пространство элементарных событий – это бесконечное несчетное множество.
Рассмотри на
плоскости некоторую область
![]() ,
имеющую площадь
,
имеющую площадь
![]() ,
и внутри ее область D
с площадью
,
и внутри ее область D
с площадью
![]() .
.
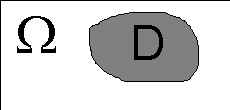
В области
![]() случайно выбирается точка X.
При этом попадание точки X
в область
случайно выбирается точка X.
При этом попадание точки X
в область
![]() - это достоверное событие, а в область
D
– случайное.
- это достоверное событие, а в область
D
– случайное.
Все точки из
![]() - равноправны, т.е. вероятность попасть
в D
пропорционально площади этой области
и не зависит от ее расположения и формы.
- равноправны, т.е. вероятность попасть
в D
пропорционально площади этой области
и не зависит от ее расположения и формы.
Определение.
Геометрической
вероятностью события
A
называется отношение площади D
к площади
![]() .
.
![]() (1)
(1)
Это правило применимо и для объемных объектов.
Аксиоматическое определение вероятности.
Совокупность S
подмножеств множества
![]() называется алгеброй, если выполняются
следующие условия:
называется алгеброй, если выполняются
следующие условия:
-
 ,
,
 .
. -
 ,
то и
,
то и
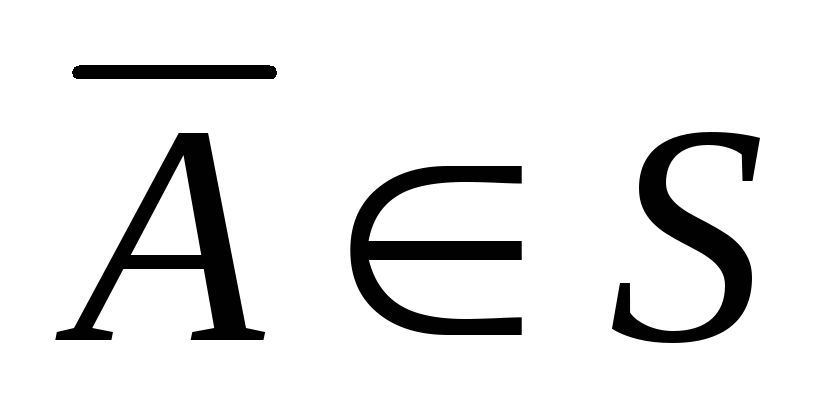 .
. -
 ,
,
 ,
то и
,
то и
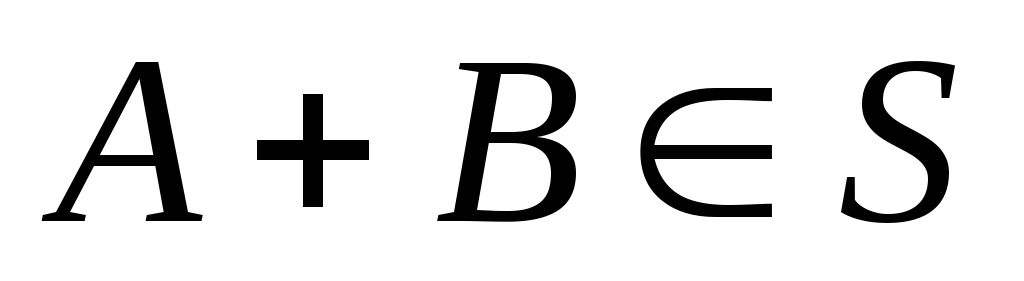 ,
,
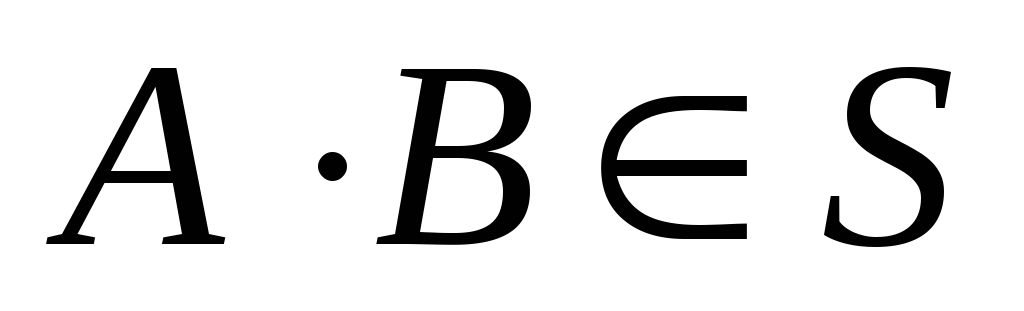 .
.
Определение.
Вероятностью называется функция
![]() ,
определенная на алгебре событий S,
принимающая действительные значения
и удовлетворяющая следующим аксиома:
,
определенная на алгебре событий S,
принимающая действительные значения
и удовлетворяющая следующим аксиома:
-
Неотрицательность.
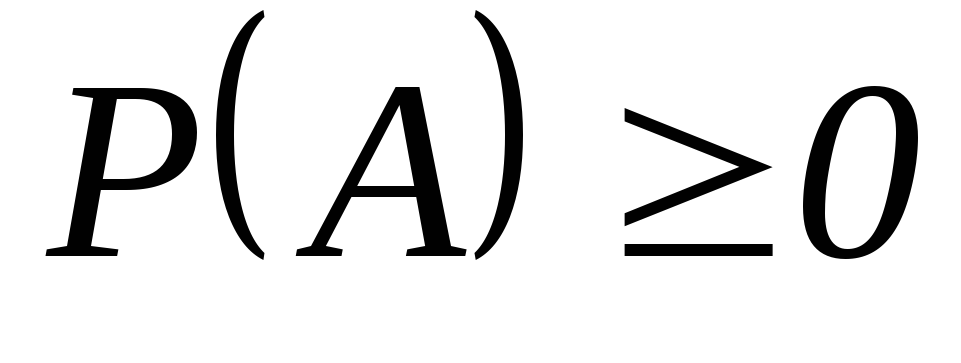 ,
, -
Нормированность.
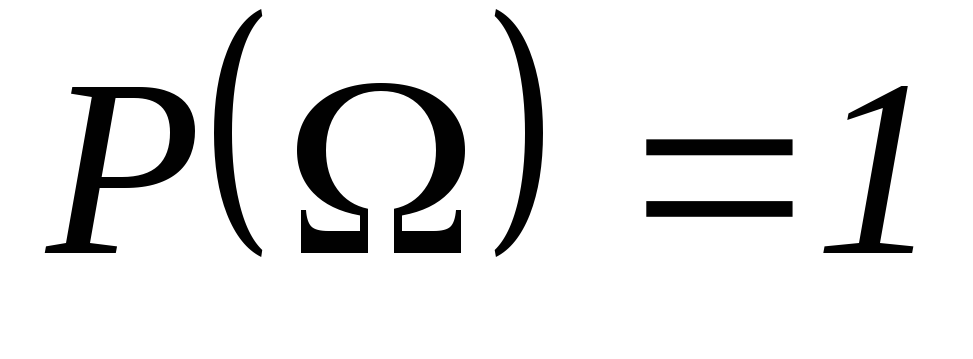 ,
, -
Аддитивность.
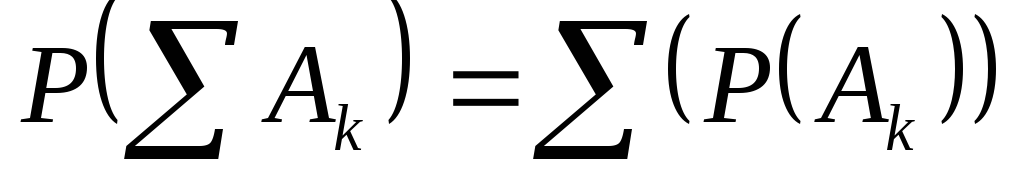 ,
,
при условии
![]() .
.
Совокупность
объектов (![]() ,
S,
P),
где
,
S,
P),
где
![]() - это пространство элементарных событий,
S
– это алгебра событий, P
– числовая функция, удовлетворяющая
аксиомам, называется вероятностным
случаем эксперимента.
- это пространство элементарных событий,
S
– это алгебра событий, P
– числовая функция, удовлетворяющая
аксиомам, называется вероятностным
случаем эксперимента.
Свойства вероятности:
-
Вероятность невозможного события равна нулю.
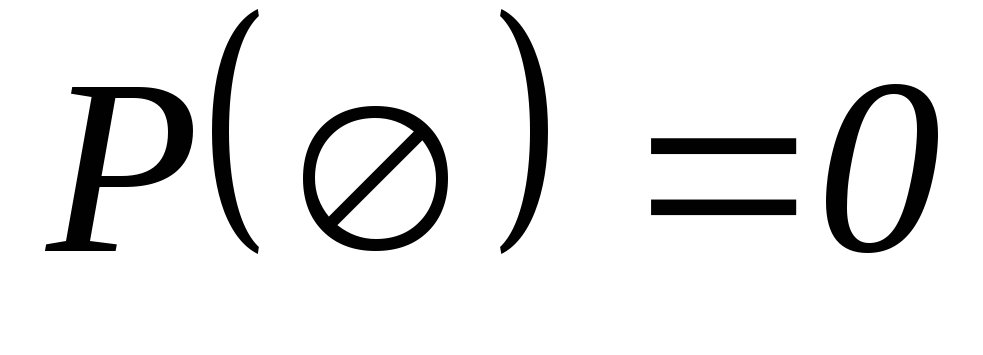 .
. -
Сумма вероятностей противоположных событий равна 1.
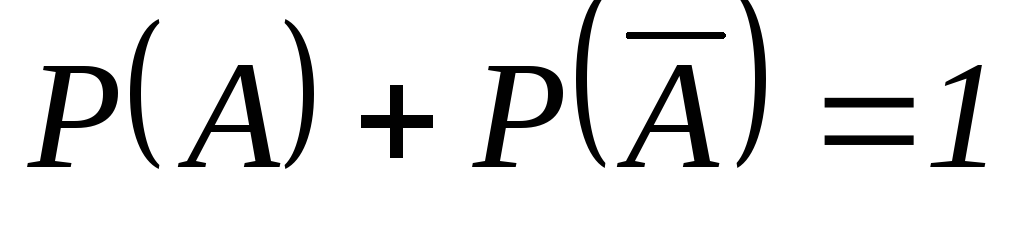 .
. -
Вероятность любого события не может быть больше 1.
-
Если событие A влечет событие B, то вероятность A меньше вероятности B.
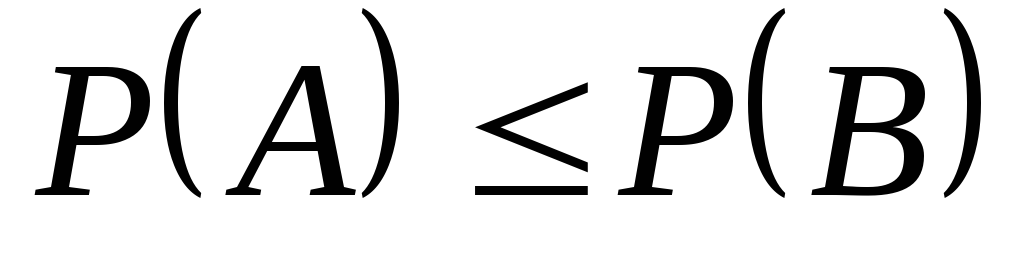 .
. -
Если события
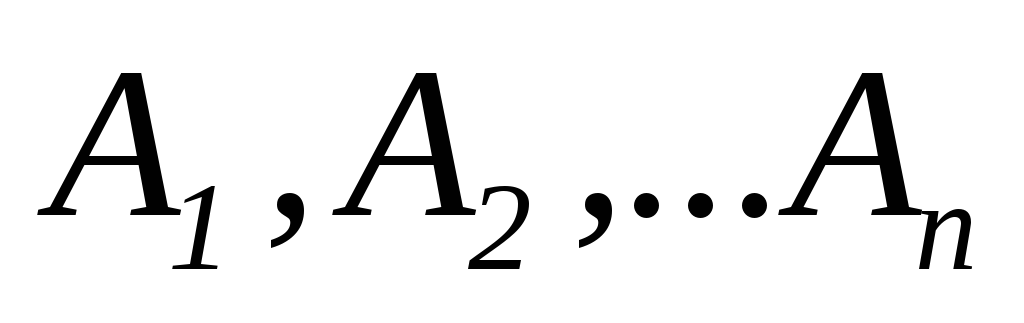 образуют полную группу несовместных
событий, т.е.
образуют полную группу несовместных
событий, т.е.
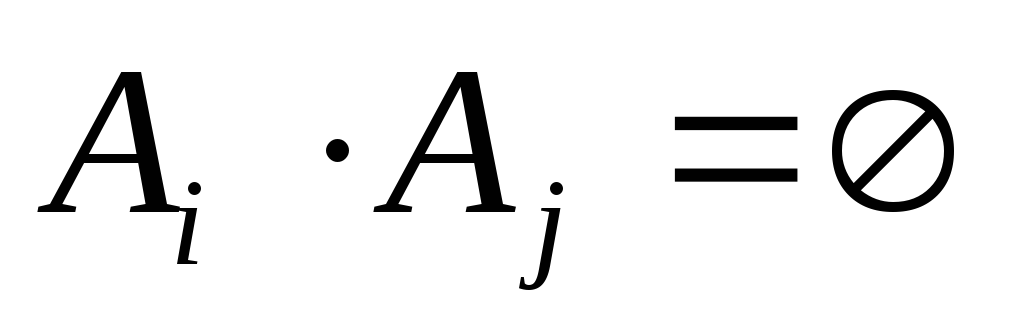 ,
то сумма их вероятностей равна 1.
Поскольку
,
то сумма их вероятностей равна 1.
Поскольку
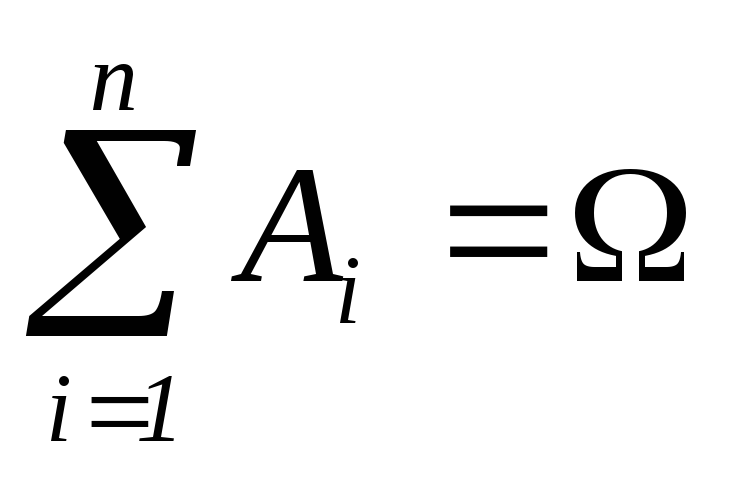 ,
то
,
то
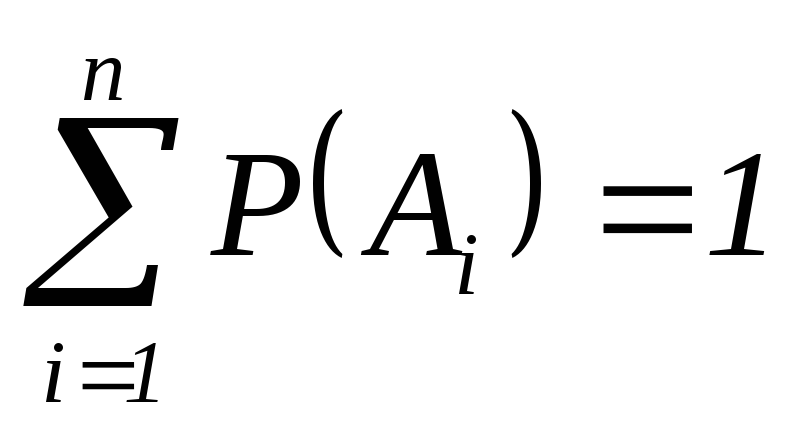 .
.
