26. Случайные события. Операции. (Теоретико-множественная трактовка).

Пусть производится некоторый опыт со случайным исходом. Пространство множества всех возможных взаимоисключающих исходов данного опыта элементарных событий обозначим как , а сами исходы – .

Случайным событием A называется любое подмножество , если - конечно или счетно, т.е. элементы множества можно пронумеровать с помощью множества натуральных чисел. .

Элементарное событие, входящее в множество A подмножества называется благоприятствующими событию A.

Множество называется достоверным событием.

 называется невозможным событием.

Над событиями можно проводить все операции, выполняемые для множеств:

1. Сумма. Если 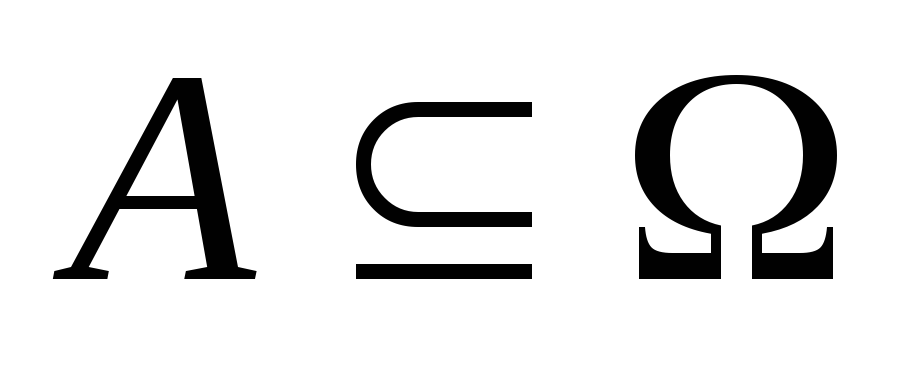и , то 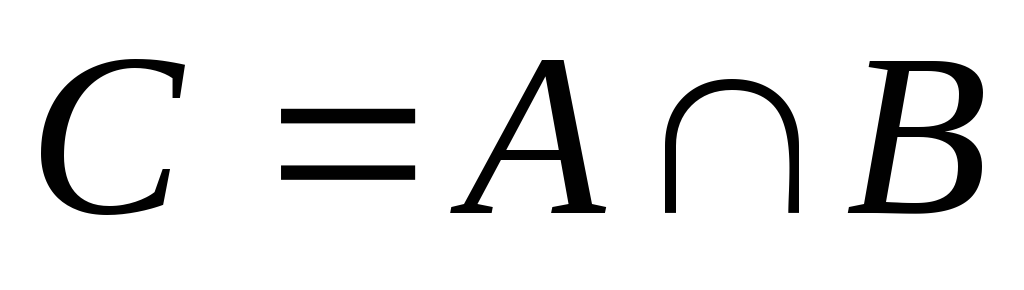- это множество, которое содержит элементы, принадлежащие хотя бы одному событию A или B.

2. Произведение двух событий A и B – это множество, которое содержит элементы общие для событий A и B.

3. Разностью двух событий A и B называется множество, которое содержит элементы события A, не принадлежащие B.

4. Противоположное событию A есть событие .

5. Событие A влечет событие B, если каждые элементы события A содержатся в B.

6. События A и B называется несовместимыми, если их произведение есть невозможное событие. .

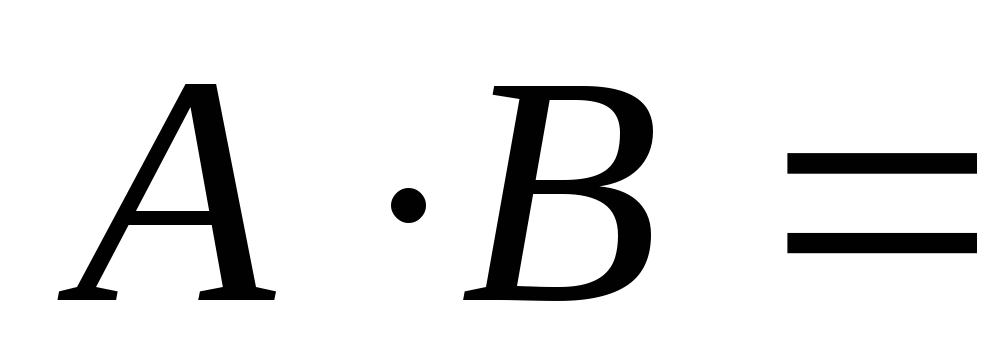7. События 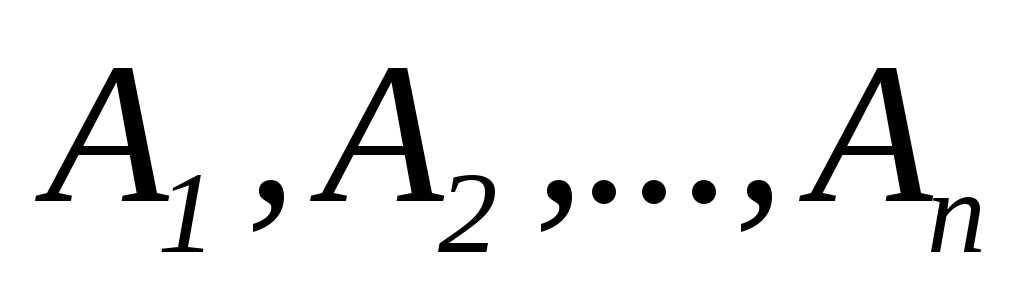образуют полную группу несовместимых событий, если выполняется следующее условие

и .

В случае несчетного пространства в качестве событий рассматриваются не все подмножества , а лишь некоторые классы этих подмножеств.

27. Относительная частота. Свойства. Статистическое и классическое определение вероятности.

Определение. Пусть в n повторяющихся опытах некоторое событие A наступило раз. Число называется частотой события A.

Определение. Отношение называется относительной частотой события A в рассматриваемой серии опытов.

Свойства относительной частоты.

1. Частота любого события заключена между 0 и 1.

2. Частота невозможного события равна 0. .

3. Частота достоверного события равна 1. .

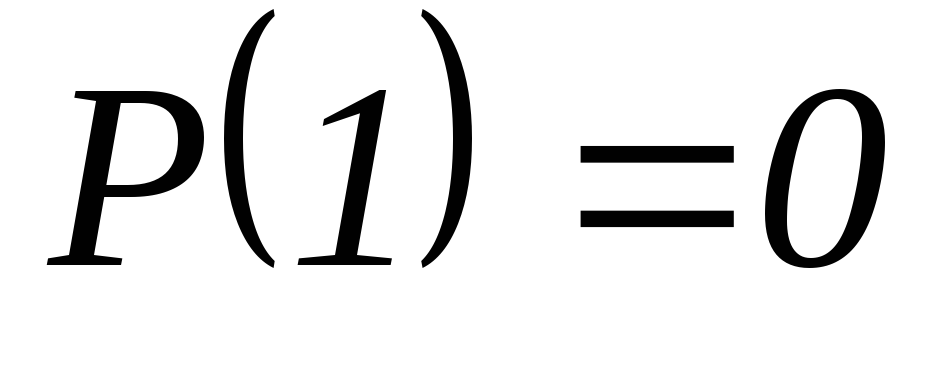4. Частота суммы двух несовместимых событий равна сумме частот этих событий.

при .

5. Свойство статистической устойчивости: с увеличением числа опытов частота принимает значения близкие к некоторому постоянному числу.

Статистическое определение вероятности.

Определение. Вероятность события – это число, выражающее степень возможности появления события в рассматриваемом опыте.

Определение. Статистической вероятностью события A называется число, около которого колеблется частота события A при достаточно большом числе испытаний.

Вероятность обозначается (1).

Свойства вероятности аналогичны свойствам относительной частоты.

Классическое определение вероятности.

Пусть проводится опыт с n исходами, которые можно представить в виде полной группы равновозможных несовместимых событий. Исходы называются случаями, опыт классическим опытом. Случай, который приводит к наступлению события A, называется благоприятствующим.

Определение. Вероятностью события A называется отношение числа m случаев, благоприятствующих этому событию к общему числу n случаев, т.е.

(2)

Свойства классической вероятности:

1. 

2. 

3. 

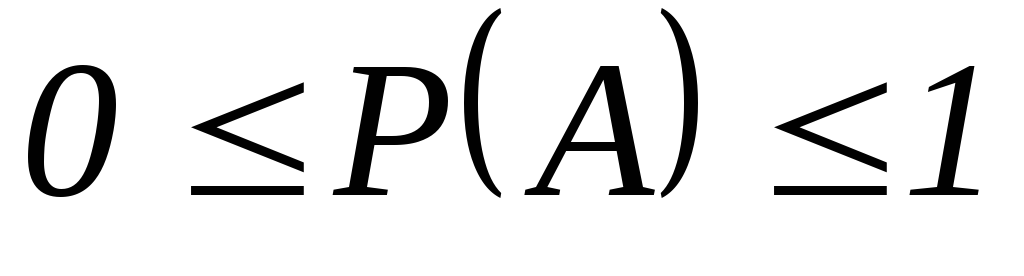
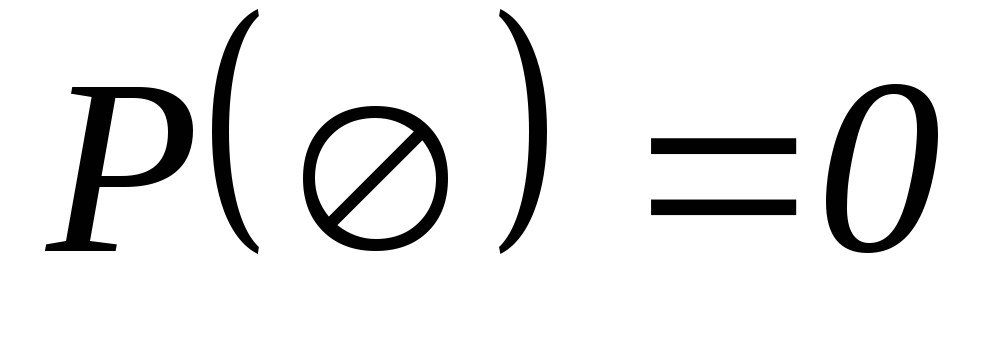
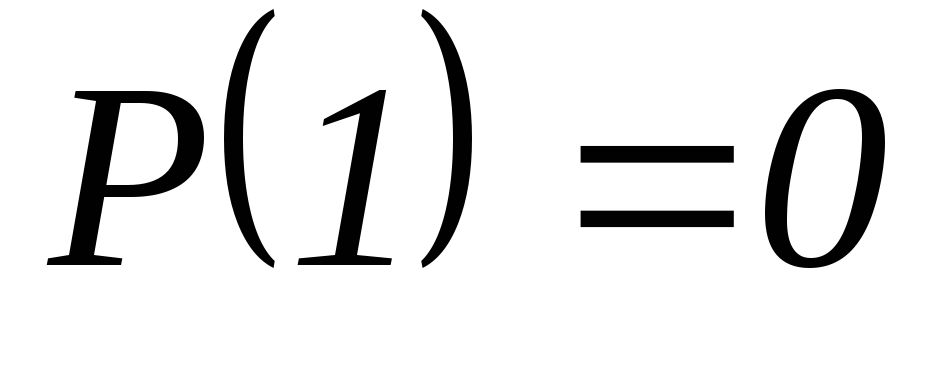
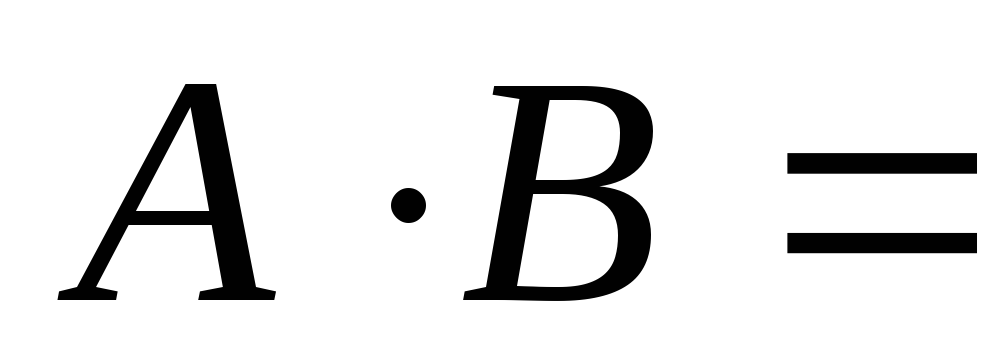
4. Если , то .
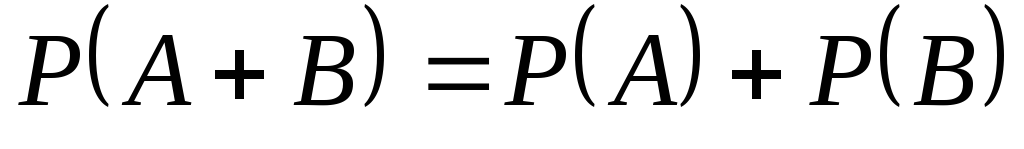