
- •21. Функции. Понятие. Классификация.
- •22. Предел последовательности и его свойства.
- •23. Неопределенный интеграл и его свойства.
- •24. Определенный интеграл и его свойства.
- •25. Случайные события. Действия. Свойства.
- •26. Случайные события. Операции. (Теоретико-множественная трактовка).
- •27. Относительная частота. Свойства. Статистическое и классическое определение вероятности.
- •28. Элементы комбинаторики. Схема выбора без возвращения.
- •Число различных размещений из n элементов по m элементов определяется с помощью формулы
- •29. Элементы комбинаторики. Схема выбора с возвращением.
- •30. Геометрическое определение вероятности. Аксиоматическое определение вероятности.
23. Неопределенный интеграл и его свойства.
Определение.
Функция
![]() называется первообразной
функцией
для данной функции
называется первообразной
функцией
для данной функции
![]() (или, короче, первообразной данной
функции) на данном промежутке, если на
этом промежутке
(или, короче, первообразной данной
функции) на данном промежутке, если на
этом промежутке
![]() .
.
Определение.
Выражение
![]() ,
где
,
где
![]() – первообразная функции
– первообразная функции
![]() и C
– произвольная постоянная, называется
неопределенным
интегралом
от функции
и C
– произвольная постоянная, называется
неопределенным
интегралом
от функции
![]() и обозначается символом
и обозначается символом
![]() ,
причем
,
причем
![]() называется подынтегральной
функцией,
называется подынтегральной
функцией,
![]() – подынтегральным
выражением,
x
– переменной
интегрирования,
знак
– подынтегральным
выражением,
x
– переменной
интегрирования,
знак
![]() –
знаком
интеграла.
–
знаком
интеграла.
Теорема.
Если функция
![]() непрерывна на сегменте
непрерывна на сегменте
![]() ,
то на этом сегменте у функции
,
то на этом сегменте у функции
![]() существует первообразная.
существует первообразная.
Свойства неопределенного интеграла.
Из определения неопределенного интеграла непосредственно вытекает следующие свойства:
-
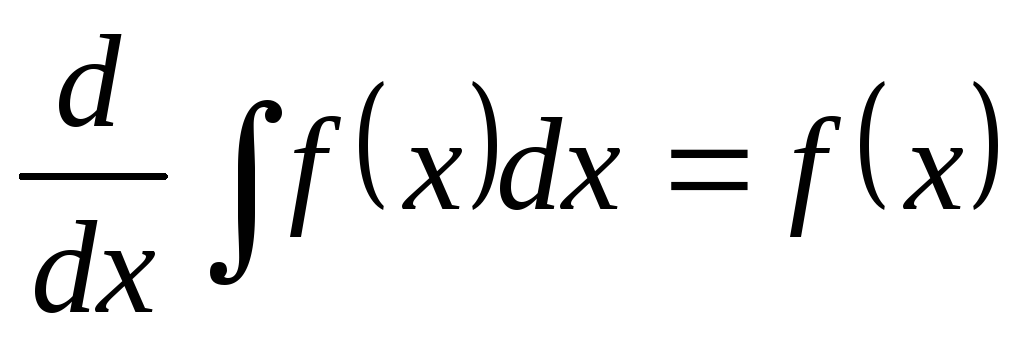 и, значит,
и, значит,
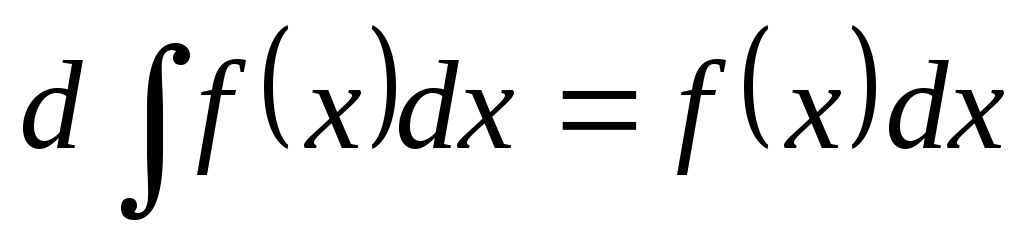 .
. -
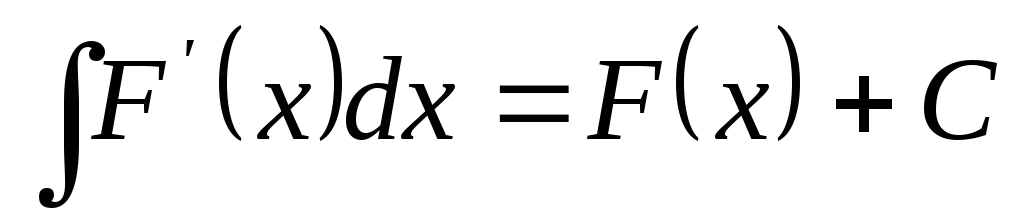 ,
что может быть переписано так:
,
что может быть переписано так:
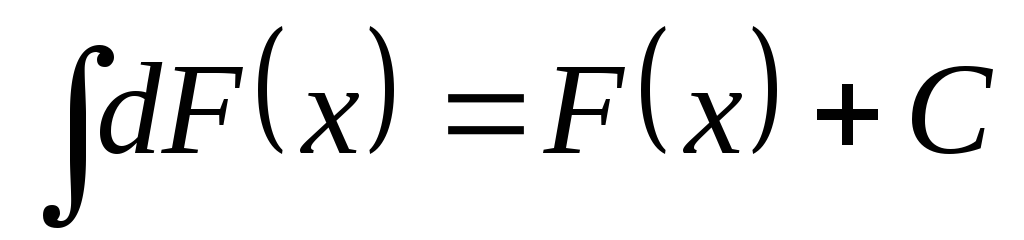 .
. -
Постоянный множитель можно выносить за знак интеграла:
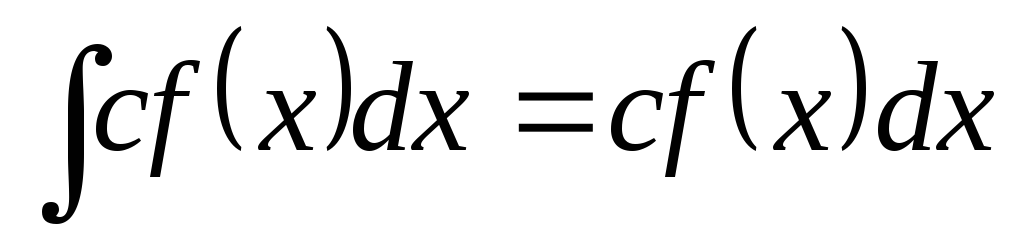 .
. -
Интеграл от суммы двух функций равен сумме интегралов от этих функций:
![]()
24. Определенный интеграл и его свойства.
З адача
о площади криволинейной трапеции. Пусть
требуется найти площадь плоской фигуры,
ограниченной графиком функции
адача
о площади криволинейной трапеции. Пусть
требуется найти площадь плоской фигуры,
ограниченной графиком функции
![]() ,
непрерывной и неотрицательной на
сегменте
,
непрерывной и неотрицательной на
сегменте
![]() ,
и отрезками
прямых y
= 0, x
= a,
x
= b.
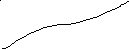
Эта фигура называется криволинейной
трапецией.
,
и отрезками
прямых y
= 0, x
= a,
x
= b.
Эта фигура называется криволинейной
трапецией.
y
 B
B




 A
A

![]()

0 a ![]()
![]()
![]() b x
b x
Разобьем отрезок
![]() точками
точками
![]() на число n
частичных отрезков и положим
на число n
частичных отрезков и положим
![]() ,
k
= 1, 2, …, n.
Наибольшую из этих разностей через
,
k
= 1, 2, …, n.
Наибольшую из этих разностей через
![]() .
На каждом частичном сегменте
.
На каждом частичном сегменте
![]() ,
k
= 1, 2, …, n,
выберем произвольную точку
,
k
= 1, 2, …, n,
выберем произвольную точку
![]() ,
,
![]() .
Произведение
.
Произведение
![]() даст площадь прямоугольника, имеющего
основание
даст площадь прямоугольника, имеющего
основание
![]() и высоту
и высоту
![]() ,
а сумма
,
а сумма
![]() - приближенную площадь S
криволинейной трапеции aABb.
Отсюда, площадь равна:
- приближенную площадь S
криволинейной трапеции aABb.
Отсюда, площадь равна:
![]() (1)
(1)
Определение.
Если существует предел (1), не зависящий
от способа разбиения отрезка
![]() и выбора точек
и выбора точек
![]() ,
то этот предел будем называть определенным
интегралом
функции
,
то этот предел будем называть определенным
интегралом
функции
![]() на сегменте
на сегменте
![]() и обозначать символом
и обозначать символом
![]() (2)
(2)
Функция
![]() в этом случае называется интегрируемой
на отрезке
в этом случае называется интегрируемой
на отрезке
![]() .
При этом
.
При этом
![]() называется подынтегральной
функцией,
называется подынтегральной
функцией,
![]() - подынтегральным
выражением,
числа a
и b
– пределами
интегрирования
(a
– нижний
предел, b
– верхний
предел),
сумма
- подынтегральным
выражением,
числа a
и b
– пределами
интегрирования
(a
– нижний
предел, b
– верхний
предел),
сумма
![]() - интегральной
суммой.
- интегральной
суммой.
Теорема.
Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
то она интегрируема на нем.
,
то она интегрируема на нем.
Свойства определенного интеграла.
1. Постоянный множитель можно выносить за знак определенного интеграла.
![]() .
.
2. Определенный интеграл от суммы двух функций равен сумме определенных интегралов от этих функций.
![]() .
.
3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный
![]() .
.
4. Интеграл по сегменту равен сумме интегралов по его частям
![]() ,
где
a
< c < b.
,
где
a
< c < b.
25. Случайные события. Действия. Свойства.
Теория вероятностей – это математическая наука, изучающая закономерности, присущие массовым случайным явлениям.
Предмет теории вероятности – это математические модели случайных явлений.
Случайное явление – это явление, предсказать исход которого невозможно.
Цель теории вероятности – это осуществление прогноза в области случайных явлений.
Случайным событием называется любой исход опыта, который может произойти или не произойти. Случайные события обозначаются A, B, C, D, … .
Непосредственные
исходы опыта называются элементарными
событиями
и обозначаются
![]() .
.
Множество всех
элементарных событий называется
пространством
элементарных событий
и обозначается
![]() .
.
Событие называется достоверным, если оно обязательно наступит в результате опыта.
Событие называется невозможным, если оно заведомо не произойдет во время опыта.
Два события называются несовместимыми, если появление одного из них исключает появление другого в одном и том же опыте, т.е. не они не могут произойти вместе в одном опыте. В противном случае события называются совместимыми.
События
![]() называются попарно несовместимыми,
если любые два из них несовместимы.
называются попарно несовместимыми,
если любые два из них несовместимы.
Несколько событий образуют полную группу, если они попарно несовместимы и в результате каждого опыта происходит одно и только одно из них.
Несколько событий называются равновозможными, если в результате опыта все события имеют равные шансы.
Действия над событиями.
Суммой двух событий A и B называется событие C = A + B, состоящее в наступлении одного из них.
Произведением событий A и B называется событие C = A · B, состоящее в совместном наступлении этих событий.
Разностью событий A и B называется событие C = A – B, происходящее тогда и только тогда, когда происходит событие A, но не происходит событие B.
Противоположным
событию A
называется событие
![]() ,
которое происходит тогда и только тогда,
когда не происходит событие A.
,
которое происходит тогда и только тогда,
когда не происходит событие A.
Событие A
влечет событие B,
если из того, что происходит событие A
следует, что происходит событие B.
![]() .
.
Если A влечет B и B влечет A, то события A и B называются равными. A = B.
Свойства операций над событиями.
-
Переместительное.
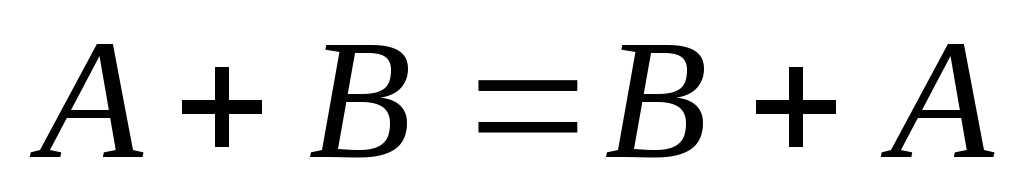 ,
,
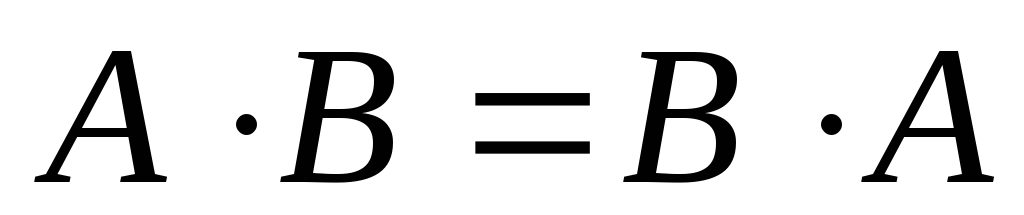 .
. -
Распределительное.
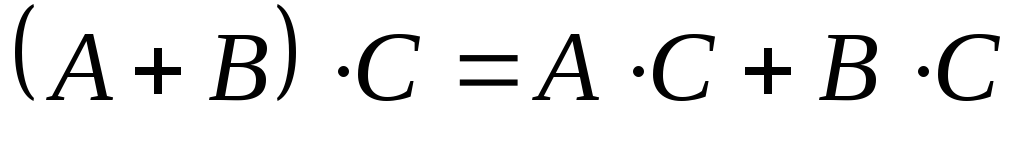 ,
,
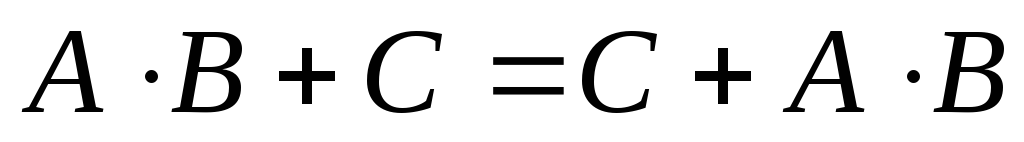 .
. -
Сочетательное.
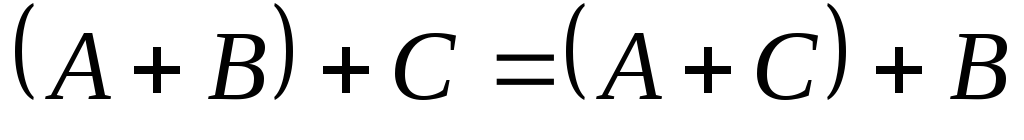 .
. -
 ,
,
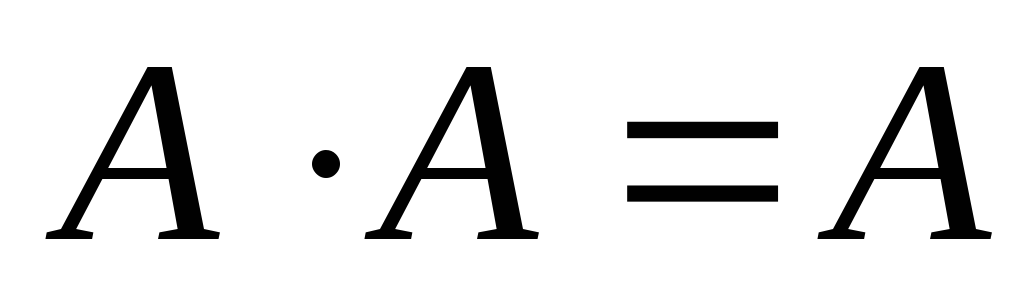
-
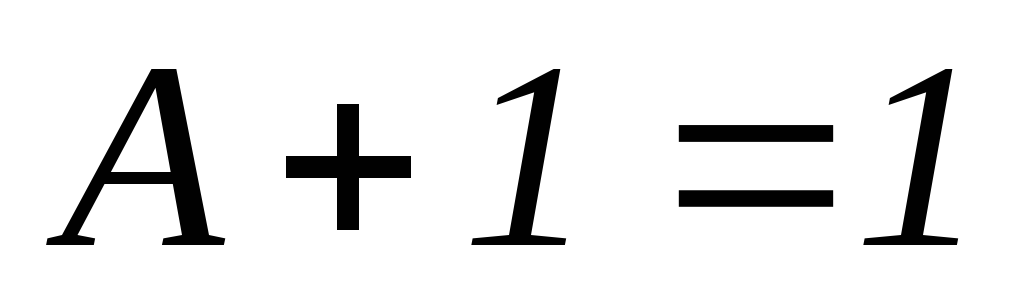 ,
,
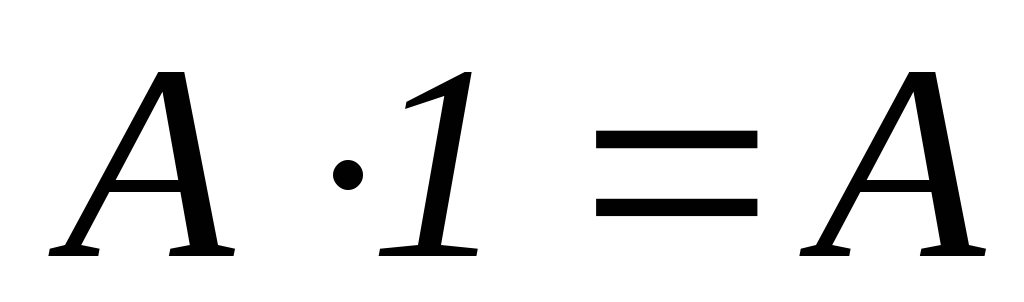
-
=1,
 = .
= . -
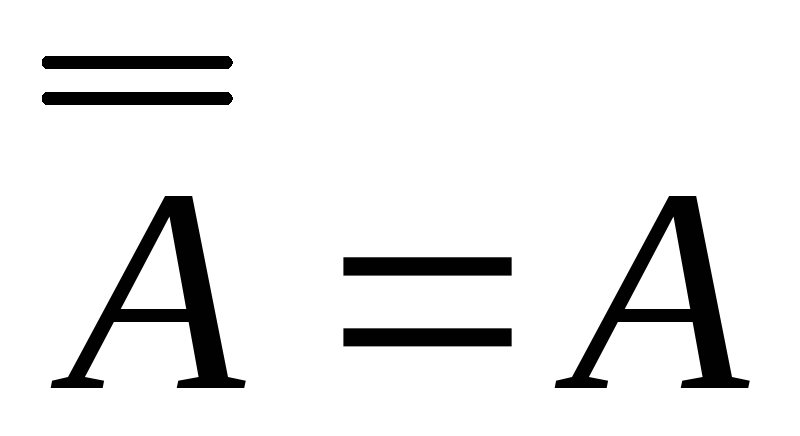 .
. -
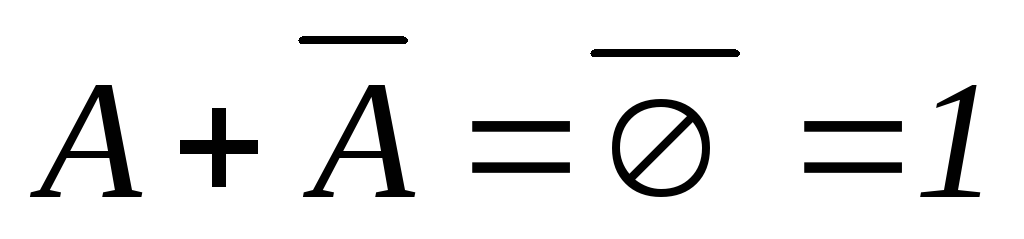 .
. -
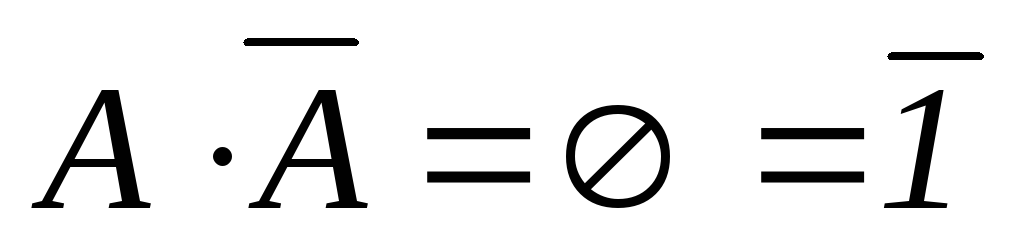 .
. -
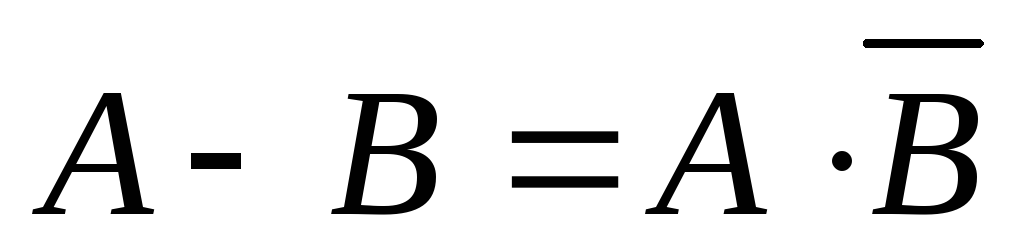
Законы де Моргана
-
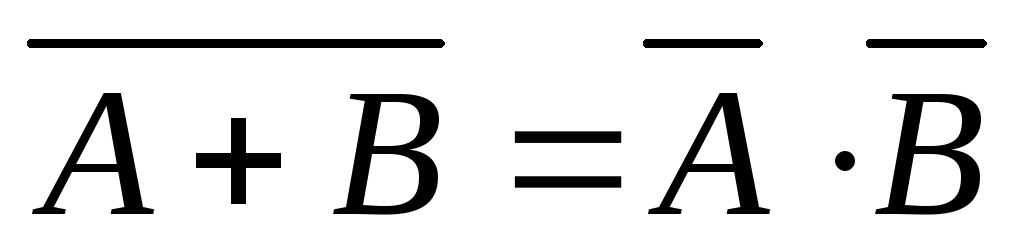 .
. -
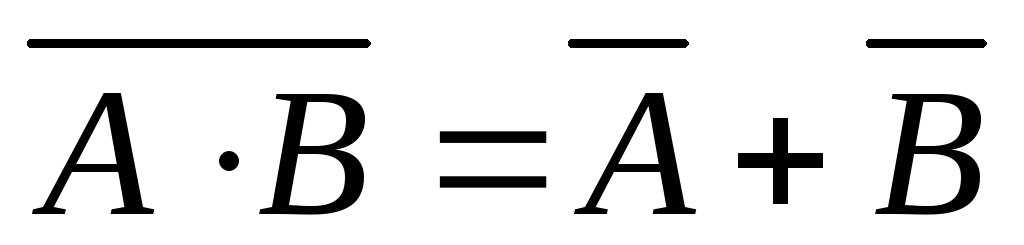 .
.
