
- •21. Функции. Понятие. Классификация.
- •22. Предел последовательности и его свойства.
- •23. Неопределенный интеграл и его свойства.
- •24. Определенный интеграл и его свойства.
- •25. Случайные события. Действия. Свойства.
- •26. Случайные события. Операции. (Теоретико-множественная трактовка).
- •27. Относительная частота. Свойства. Статистическое и классическое определение вероятности.
- •28. Элементы комбинаторики. Схема выбора без возвращения.
- •Число различных размещений из n элементов по m элементов определяется с помощью формулы
- •29. Элементы комбинаторики. Схема выбора с возвращением.
- •30. Геометрическое определение вероятности. Аксиоматическое определение вероятности.
Темы вопросов
21. Функции. Понятие. Классификация. 2
22. Предел последовательности и его свойства. 3
23. Неопределенный интеграл и его свойства. 5
24. Определенный интеграл и его свойства. 6
25. Случайные события. Действия. Свойства. 8
26. Случайные события. Операции. (Теоретико-множественная трактовка). 10
27. Относительная частота. Свойства. Статистическое и классическое определение вероятности. 11
28. Элементы комбинаторики. Схема выбора без возвращения. 12
29. Элементы комбинаторики. Схема выбора с возвращением. 13
30. Геометрическое определение вероятности. Аксиоматическое определение вероятности. 14
21. Функции. Понятие. Классификация.
Определение. Пусть X – некоторое числовое множество, в котором каждому элементу x из множества X по какому-либо закону поставлено одно и только одно значение y из множества Y.
Тогда будем
говорить, что определена функциональная
зависимость
y
от x
по закону
![]() .
.
При этом x называют независимой переменной (аргументом), а y – зависимой переменной или функцией, множество X – областью определения функции, а множество Y – областью значений.
Совокупность точек
xOy,
удовлетворяющих уравнению
![]() называется графиком
функции.
Задать функцию – это значит указать
закон, по которому каждому значению из
области определения соответствует
значение из области значений.
называется графиком
функции.
Задать функцию – это значит указать
закон, по которому каждому значению из
области определения соответствует
значение из области значений.
Способы задания функции:
-
табличный,
-
аналитический (в виде формул – функциональных зависимостей),
-
графический.
Следует подчеркнуть, что функция может быть задана и набором функций, например:
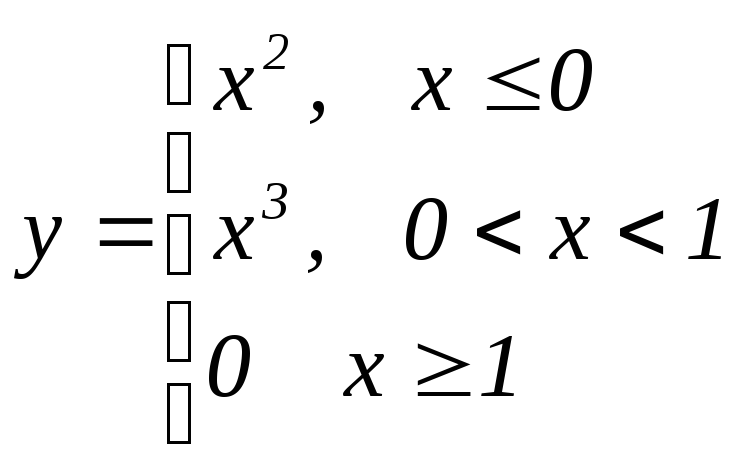
Говорят, что
![]() не убывает на множестве X,
если для любого
не убывает на множестве X,
если для любого
![]() справедливо условие
справедливо условие
![]() .
Функция
.
Функция
![]() не возрастает на множестве X,
если для любого
не возрастает на множестве X,
если для любого
![]() справедливо условие
справедливо условие
![]() .
Неубывающие и невозрастающие функции
называются монотонными.
.
Неубывающие и невозрастающие функции
называются монотонными.
Если для любого
![]() справедливо условие
справедливо условие
![]() ,
то функция называется возрастающей на
множестве X.
Если для любого
,
то функция называется возрастающей на
множестве X.
Если для любого
![]() справедливо условие
справедливо условие
![]() ,
то функция называется убывающей на
множестве X.
Такие функции называются строго
монотонными.
,
то функция называется убывающей на
множестве X.
Такие функции называются строго
монотонными.
Если на некотором
промежутке множества X
определена функция
![]() с множеством значений z
и на этом же множестве определена функция
с множеством значений z
и на этом же множестве определена функция
![]() ,
то функция
,
то функция
![]() называется сложной функцией (суперпозицией),
а переменная z
называется промежуточной.
называется сложной функцией (суперпозицией),
а переменная z
называется промежуточной.
Классификация элементарных функций:
-
Целая рациональная функция.
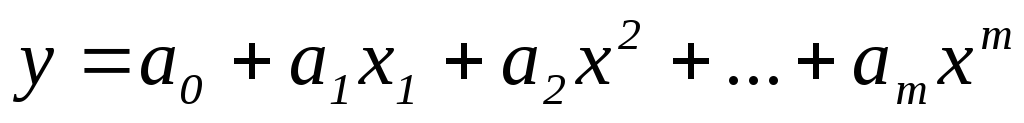 .
. -
Дробно-рациональная функция.
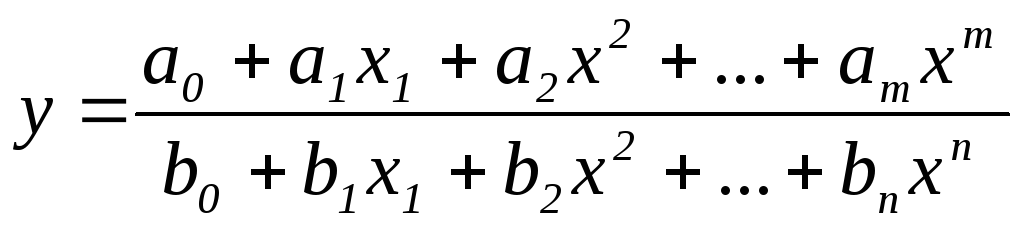 .
. -
Степенная функция.
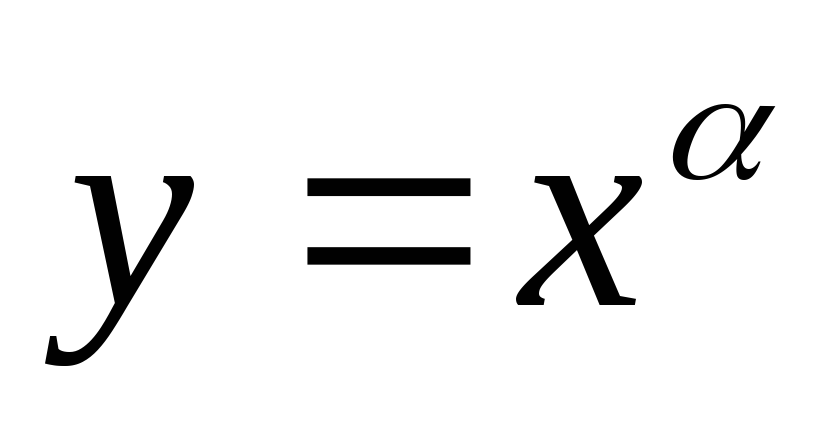 ,
где
,
где
 - действительной число.
- действительной число. -
Показательная функция.
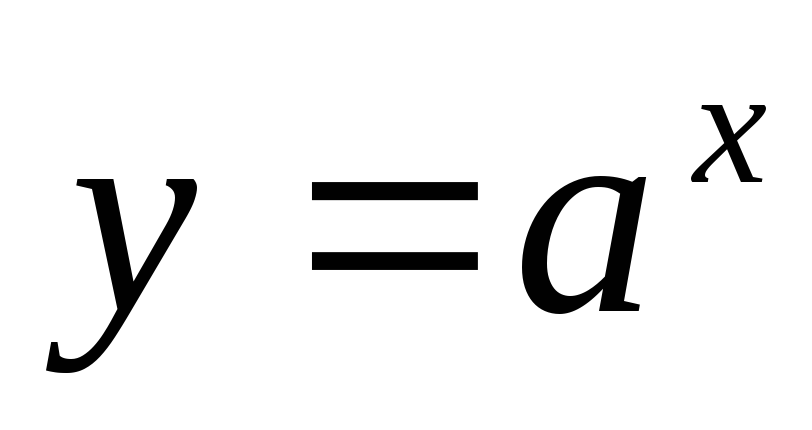 ,
где
,
где
 и
и
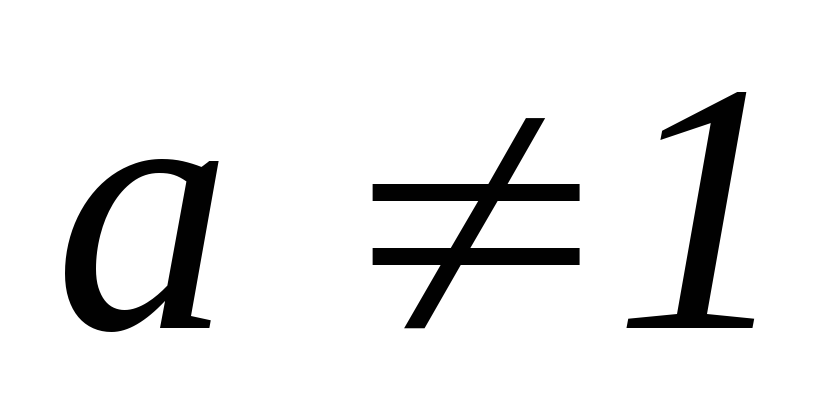 .
. -
Логарифмическая функция.
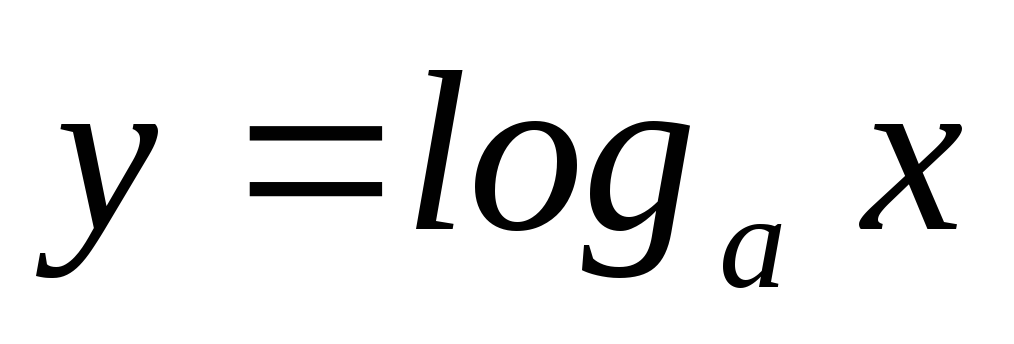 ,
где
,
где
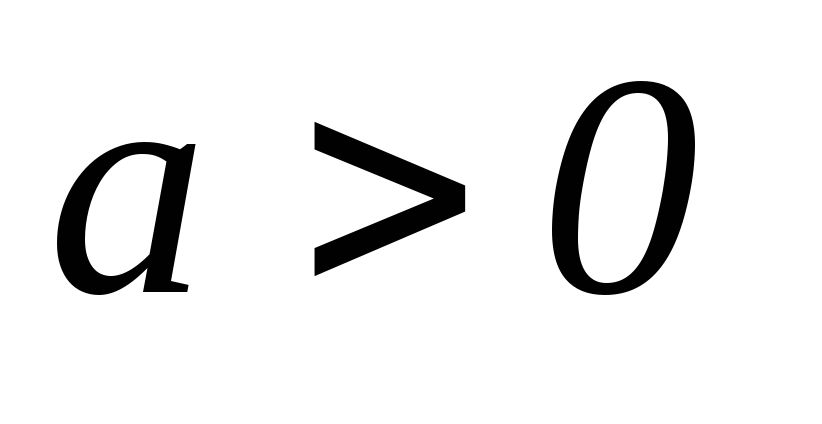 и
и
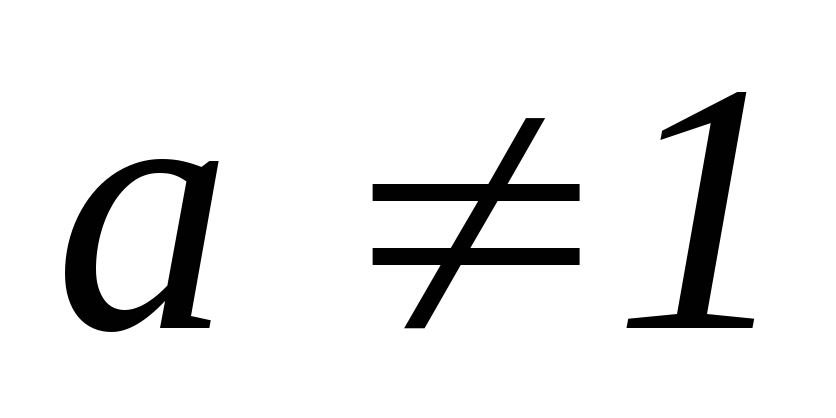 .
. -
Тригонометрические функции.
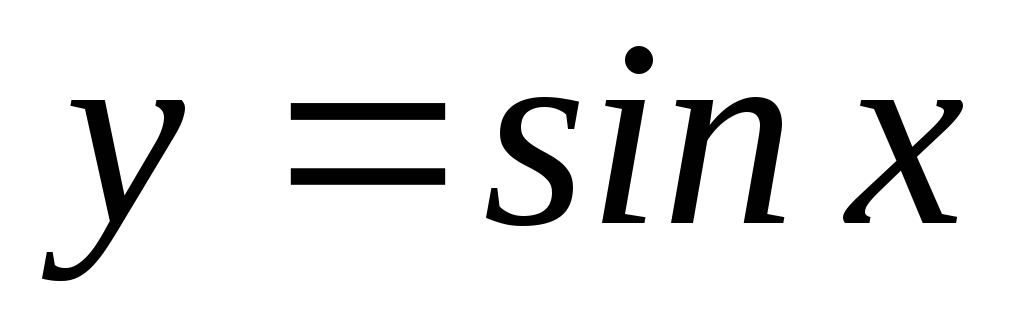 ,
,
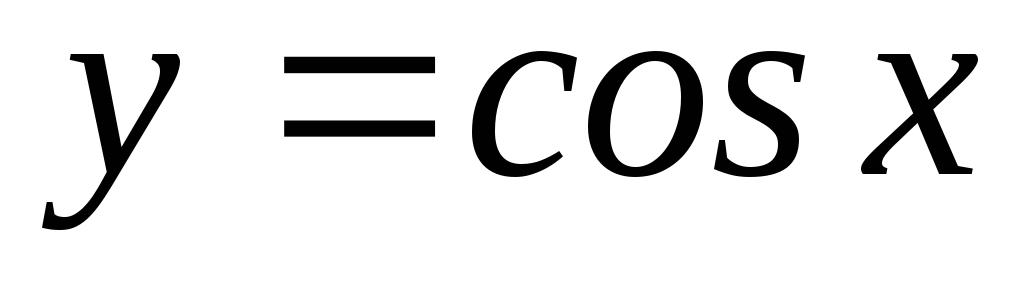 ,
,
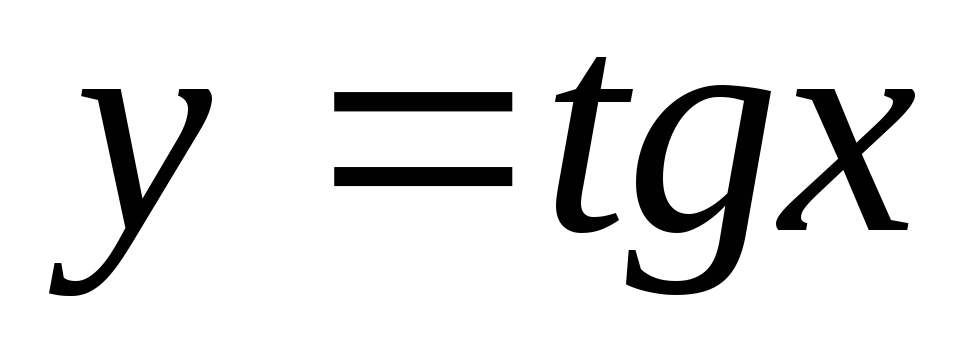 ,
,
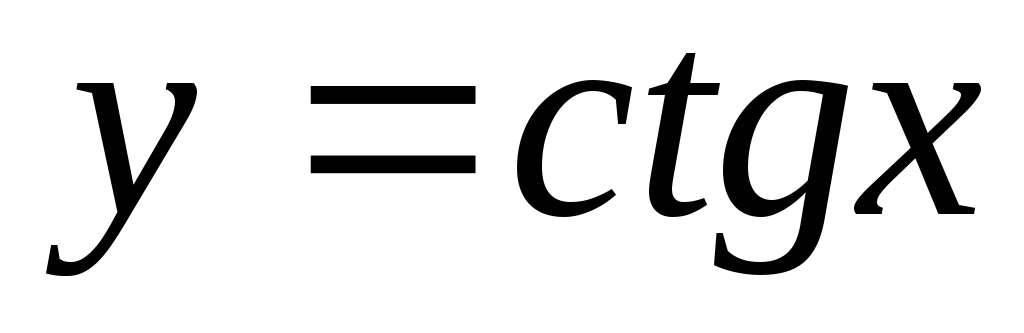 .
. -
Обратные тригонометрические функции.
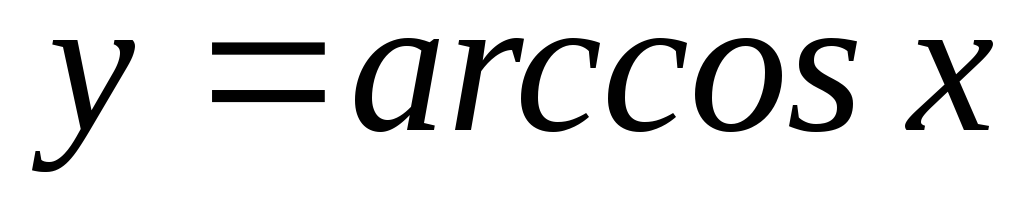 ,
,
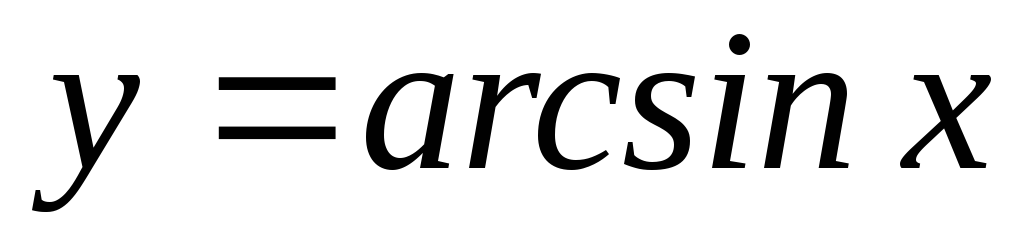 ,
,
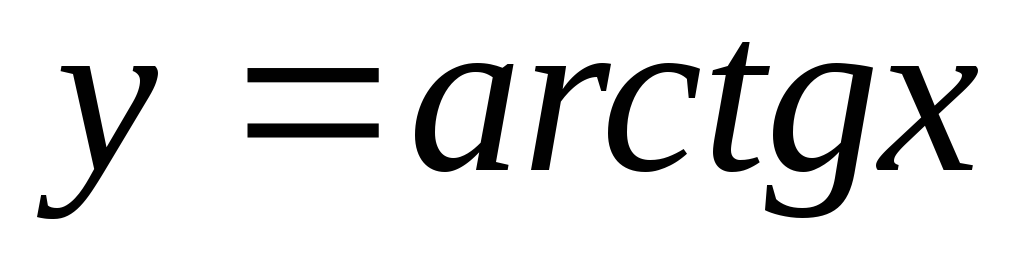 ,
,
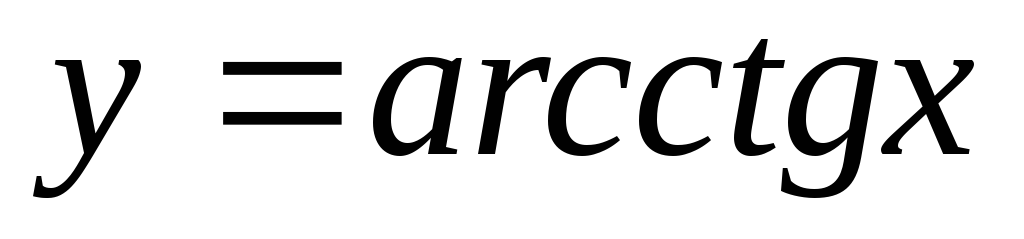 .
. -
Сложная функция.
 ,
где
,
где
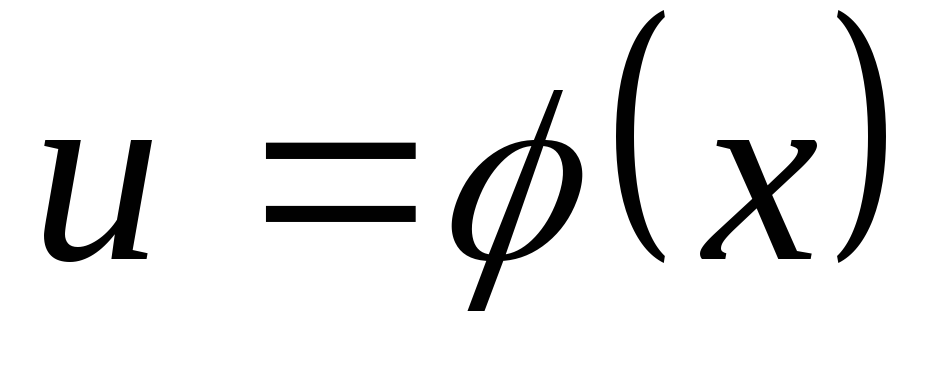 .
. -
Гармонические колебания.
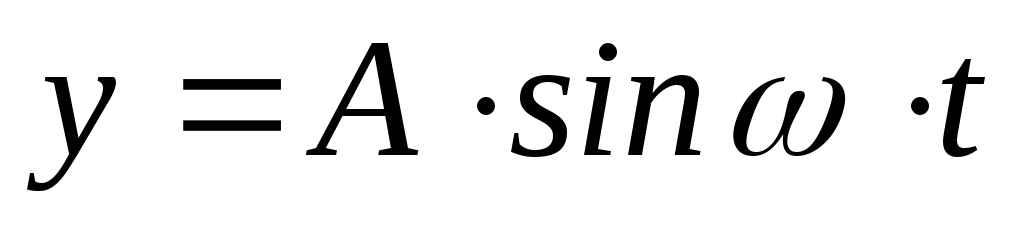 ,
где A
и
,
где A
и
 - положительные постоянные.
- положительные постоянные. -
Обратная функция.
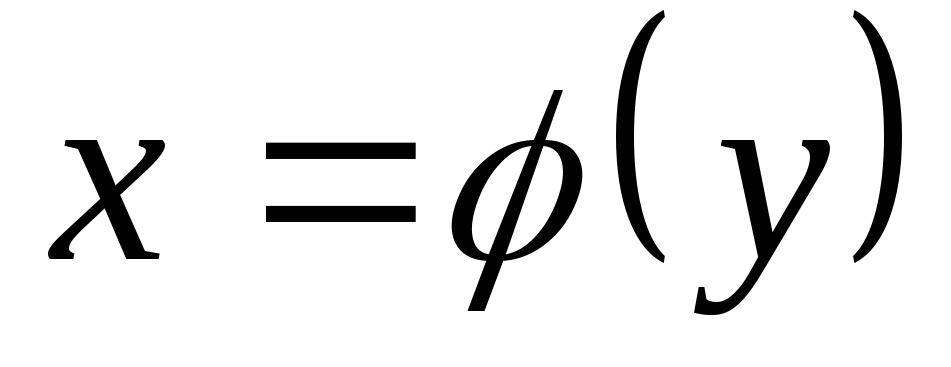 для функции
для функции
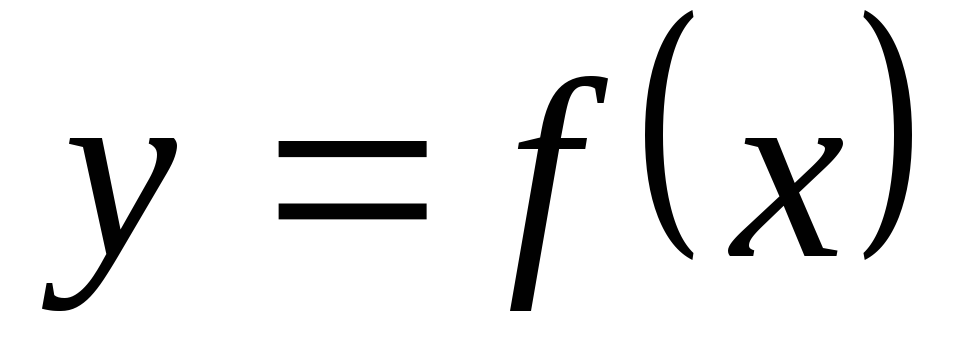 .
.
22. Предел последовательности и его свойства.
Числовые последовательности представляют собой бесконечные упорядоченные множества чисел.
Если каждому числу
n
из натурального ряда чисел поставлено
в соответствие вещественное число
![]() ,
то множество вещественных чисел
,
то множество вещественных чисел
![]() называется числовой
последовательностью.
называется числовой
последовательностью.
Числа
![]() называются элементами (членами)
последовательности. Символ
называются элементами (членами)
последовательности. Символ
![]() называется общим элементом (членом)
последовательности, а число n
– его номером.
называется общим элементом (членом)
последовательности, а число n
– его номером.
Числовая
последовательность обозначается {![]() }.
}.
Геометрически числовые последовательности вещественных чисел изображаются на оси в виде точек, координаты которых равны соответствующим членам последовательности.
Последовательность
вещественных чисел {![]() }
называется ограниченной сверху, если
существует такое число M, что любое
}
называется ограниченной сверху, если
существует такое число M, что любое
![]() этой последовательности удовлетворяет
неравенству
этой последовательности удовлетворяет
неравенству
![]() .
.
Последовательность
вещественных чисел {![]() }
называется ограниченной
снизу,
если существует такое число M,
что любое
}
называется ограниченной
снизу,
если существует такое число M,
что любое
![]() этой последовательности удовлетворяет
неравенству
этой последовательности удовлетворяет
неравенству
![]() .
.
Последовательность
{![]() }
ограничена,
если она ограничена и сверху и снизу,
т.е. существуют такие числа m
и M,
что для любого
}
ограничена,
если она ограничена и сверху и снизу,
т.е. существуют такие числа m
и M,
что для любого
![]() этой последовательности верно неравенство
этой последовательности верно неравенство
![]() .
.
Пусть
![]() ,
то для любого
,
то для любого
![]() .
.
Последовательность
{![]() }
– неограничена,
если для любого A
существует
}
– неограничена,
если для любого A
существует
![]() ,
при котором
,
при котором
![]() .
.
Предел последовательности.
Число a
называется пределом
{![]() },
если для любого
},
если для любого
![]() существует такая зависимость
существует такая зависимость
![]() ,
что при любых
,
что при любых
![]() выполняется неравенство:
выполняется неравенство:
![]() (1)
(1)
Если предел
последовательности равен числу a,
это записывается так:
![]()
Числовая
последовательность {![]() }
называется бесконечно
большой,
если для любого n
> 0 существует
такой номер
}
называется бесконечно
большой,
если для любого n
> 0 существует
такой номер
![]() ,
что
,
что
![]() .
.
Очевидно, что бесконечно большая последовательность является неограниченной.
Числовая
последовательность {![]() }
называется бесконечно
малой, если
для любого
}
называется бесконечно
малой, если
для любого
![]() существует такая зависимость
существует такая зависимость
![]() ,
что при
,
что при
![]() ,
выполняется
,
выполняется
![]() .
.
Основные свойства бесконечно малых последовательностей.
-
Суммой или разностью двух бесконечно малых последовательностей является бесконечно малая последовательность.
Следствие. Сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
-
Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Следствие. Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
-
Произведение бесконечно малой последовательности на ограниченную является бесконечно малая последовательность.
Следствие. Произведение бесконечно малой последовательности на постоянное число является бесконечно малой последовательностью.
Сходящиеся последовательности.
Числовая
последовательность {![]() }
называется сходящейся,
если существует такое число a,
что для любого
}
называется сходящейся,
если существует такое число a,
что для любого
![]() все находящиеся в окрестности элементы
этой последовательности начиная с
некоторого номера меньше a.
все находящиеся в окрестности элементы
этой последовательности начиная с
некоторого номера меньше a.
Таким образом, последовательность, имеющая конечный предел, является сходящейся, а последовательность, не имеющая предела, является расходящейся.
Следствия.
-
Бесконечно большая последовательность не имеет предела.
-
Всякая бесконечно малая последовательность сходится и имеет своим пределом a = 0.
-
Предел последовательности, у которой все члены равны числу C, где C – константа, равен C.
Основные свойства сходящихся последовательностей.
-
Если все элементы бесконечно малой последовательности равны одному и тому же числу C, то предел этой последовательности – C.
-
Сходящаяся последовательность имеет только один предел.
-
Предел суммы двух или нескольких сходящихся последовательностей равен сумме пределов этих последовательностей.
-
Предел произведения сходящихся последовательностей равен произведению пределов.
-
Предел частного сходящихся последовательностей равен частному пределов, если предел знаменателя не равен нулю.
Монотонные последовательности.
![]() (1) возрастающая строго
монотонная
(1) возрастающая строго
монотонная
![]() (2) неубывающая
строго монотонная
(2) неубывающая
строго монотонная
![]() (3) убывающая
(3) убывающая
![]() (4) невозрастающая
(4) невозрастающая
Числовая
последовательность {![]() }
называется возрастающей,
если при любом n
выполняется условие (1), неубывающей
при выполнении условия (2), убывающей
при выполнении условия (3), невозрастающей
при выполнении условия (4).
}
называется возрастающей,
если при любом n
выполняется условие (1), неубывающей
при выполнении условия (2), убывающей
при выполнении условия (3), невозрастающей
при выполнении условия (4).
Монотонная ограниченная последовательность сходится.
