Глава III

МІРА ЛЕБЕГА ОБМЕЖЕНИХ МНОЖИН У

3.1. Елементарні множини та їх властивості

Означення 3.1.1 Будь-які інтервали , півінтервали або , або сегменти будемо називати відрізками і позначати літерой . При цьому у число відрізків включаємо порожню множину і сегмент, що складається з одної точки .

Означення 3.1.2 Елементарними множинами в будемо називати будь-ялі скінченні об’єднання попарно неперетинних відрізків. Зокрема, будь-який відрізок – елементарна множина.

Одже будь-яка елементарна множина має вигляд , де може бути довільним натуральним числом і відрізки попарно не перетинаються.

Властивості елементарних множин.

1. Перетин скінченної множини елементарних множин є елементарна множина.

Доведення. Твердження очевидно, якщо розглянути перетин двох відрізків. Розглянемо випадок двох множин і . Маємо .

Загальний випадок доводиться методом математичної індукції.

2. Доповнення елементарної множини до деякого відрізка є елементарною множиною.

Доведення. Твердження очевидно, якщо елементарна множина сама є інтервалом, полуінтервалом або сегментом. Загальний випадок випливає з рівності: .

3. Об’єднання скінченної множини елементарних множин є елементарна множина.

Доведення. Розглянемо випадок двох множин і . Нехай містить об’єднання . Розглянемо доповнення множини до : . Внаслідок властивостей 2 і 1 множина  елементарна. Тоді за властивостю 2,  елементарна, тому, що .

4. Різниця двох елементарних множин є елементарна множина.

Доведення. Зобразимо різницю у вигляду: , де містить об’єднання . Внаслідок властивостей 2 і 1 множина  елементарна.

5. Симетрична різниця двох елементарних множин є елементарна множина.

Ця властивість випливає з 4 і 3 , тому що .

2. . Міра елементарних множин та її властивість

Означення 3.2.1 Мірою будь якого відрізка називається його довжина. Позначається міра символом .

Тобто незалежно від того, чи буде відрізок інтервалом , сегментом , півінтервалом або , . Зокрема міра відрізку і порожньої множини дорівнює нулю.

Означення 3.2.2 Мірою будь якої елементарної множини називається сума довжин відрізків , тобто .

Розглянемо наступні властивості.

1. Якщо множини і не мають спільних елементів, то .

Доведення. Позначимо 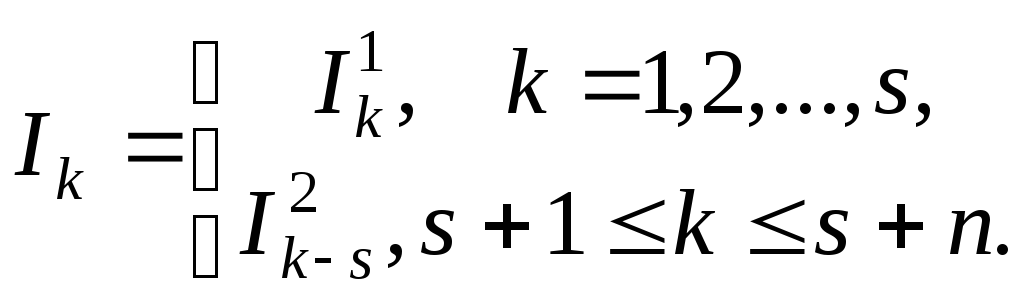Тоді

.

Методом математичної індукції ця властивість поширюється на випадок скінченної множини неперетинних елементарних множин. Ця властивість називається адитивністю міри.

Наслідок 1. Якщо і  елементарні множини і , то

. (3.2.1)

Доведення. Зобразимо множину у вигляді . В силу адитивності міри , а це еквівалентно сформулюваному.

Наслідок 2. Якщо і  елементарні множини і , то

.

Ця властивість виливає з (3.2.1), тому що , і називається монотонністю міри.

Наслідок 3. Якщо і  елементарні множини, то

(3.2.2)

Доведення. Зобразимо множину у вигляді двох неперетинних множин і далі застосуємо властивість 1 і наслідок 1:

.

Наслідок 4. Якщо елементарна множина міститься в об’єдненні скінченної множини елементарних множин , r, то

.

Доведення. Нехай 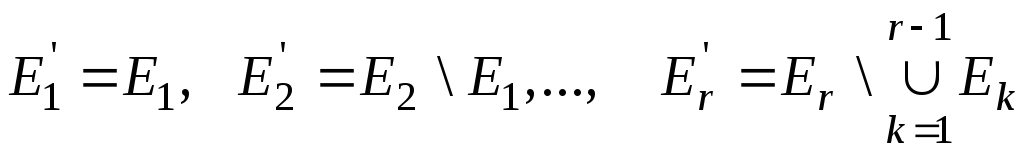. Множини попарно не перетинаються і, як легко перевірити, . Отже, внаслідок монотонності і адитивності одержимо

.

2. Якщо елементарна множина міститься в об’єдненні зчисленної множини елементарних множин , то

. (3.2.3)

Доведення. Нехай , . Для кожного відрізку і для будь-якого знайдемо сегмент такий, що і . З іншого боку для кожного відрізка і знай-демо інтервал такий, що і . Тоді

(3.2.4)

і

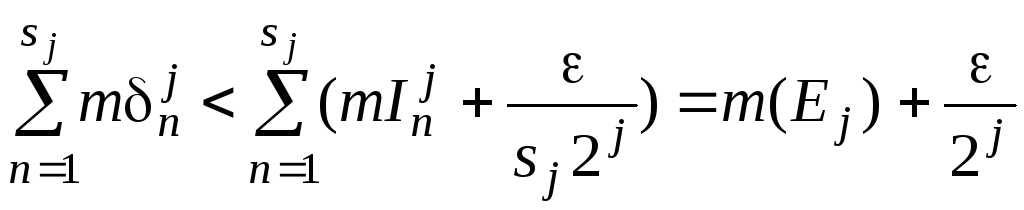. (3.2.5)

Оскільки множина міститься в об’єдненні множин , то система інтервалів покриває замкнену обмежену множину =. За лемою Гейне-Бореля існує скінченне покриття, яке позначимо через . Оскільки сегменти попарно не перетинаються, то і внаслідок нерівностей (3.2.4-3.2.5) маємо

.

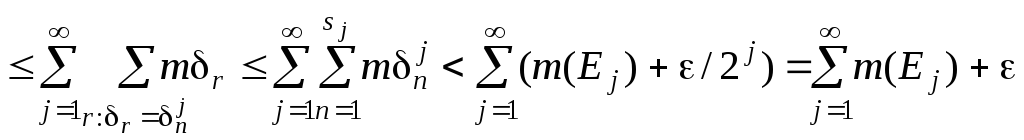Отже . Спрямувавши до нуля одержимо (3.2.3). Властивість 2 доведена.

Наслідок 4. Якщо елементарна множина є об’єднання зчисленної множини неперетинних елементарних множин , то

. (3.2.6)

Доведення. В силу (3.2.3) , а з іншого боку, тому, що елементарна множина містить елементарну множину , де довільне натуральне число, то внаслідок монотонності та адитивності міри і отже , що з раніш одержаною нерівністю доводить (3.2.6).