Властивості відкритих і замкнених множин

1. Для того щоб множина була відкритою необхідно і достатньо, щоб доповнення (доповнення до ) було замкнуто.

Доведення. Необхідність. Нехай множина відкрита і припустимо, що не містить граничну точку . Тоді і отже існує окіл такий, що , а це означає, що не містить не одної точки множини . Отже не є граничною множини , а це суперечить припущенню.

Достатність. Нехай множина замкнена і точка . Тоді існує окіл цієї точки, що не містить не одної точки множини , тому що у протилежному випадку точка була би граничною точкою множини і належала би . Отже окіл , тобто множина відкрита, що і треба було довести.

2. Об’єднання будь-якої сім’ї відкритих множин є множина відкрита.

Доведення. Нехай . Тоді і існує окіл точки такий, що . Отже множина відкрита.

3. Перетин будь-якої сім’ї замкнутих множин є множина замкнута.

Доведення. Внаслідок співвідношень двоїстості і властивостей 1 і 2 множина відкрита, отже (властивість 1) замкнена.

4. Перетин скінченного набора відкритих множин є множина відкрита.

Доведення. Нехай . Тоді для кожної множини знайдеться окіл . Покладемо . Очевидно, що для будь-якого : і .

5. Об’єднання скінченного набора замкнених множин є множина замкнена.

Доведення. В силу співвідношень двоїстості і властивостей 1 і 4 множина відкрита, отже (властивість 1) замкнена.

Покажемо на прикладах, що умова скінченнності у властивостей 3,4 не зайва.

Приклад 1. Нехай . Тоді множина і не відкрита і не замкнена.

Приклад 2. Нехай . Тоді множина і не відкрита і не замкнена.

Нехай є довільної, обмеженою знизу, замкненою множиною з простору і . Внаслідок означення точної нижньої межі для будь-якого натурального числа знайдеться елемент такий, що . Якщо серед елементів існує нескінченна множини різних, то точка є граничною точкою множини і належить . В протилежному випадку існує число таке, що для всіх елементи , отже . Аналогічно, якщо є довільної, обмеженою зверху, замкненою множиною з простору і , то .

Якщо є довільної, обмеженою, замкненою множиною з простору , то , а сегмент називається найменшим сегментом, що містить замкнену множину .

Теорема 2.1.3 (Структура відкритої обмеженої множина з простору ). Будь-яка відкрита обмежена множина є об’єднання скінченної або зчисленної множини попарно неперетинних інтервалів , кінці яких не належать множині . Інтервали називаються складовими інтервалами множини .

Доведення. Нехай . Так як множина обмежена, то множина обмежена знизу і замкнена. Тому належить , а півінтервал належить . Аналогічно множина обмежена зверху і замкнена. Тому належить , а півінтервал належить . Отже інтервал належить , а кінці його не належать . Інтервал називається складовим. Покажемо, що два довільних складових інтервалів не перетинаються. Припустимо, що знайшлись два інтервала і , що мають спільну точку , і нехай . Тоді точка і через те належить множині , а це суперечить тому, що інтервал складовий.

Покажемо, що складових інтервалів не більш ніж зчисленна множина. Для цього виберемо по раціональній точці з кожного інтервала. Оскільки інтервали не перетинаються, то ці точки різні і тому утворюють деяку підмножину множини раціональних чисел. Таким чином установлена взаємно однозначна відповідність між множиною складових інтервалів множини і множиною . Оскільки множина не більш ніж зчисленна, то і множина складових інтервалів множини не більш ніж зчисленна.

Теорема доведена.

Теорема 2.1.4 (Структура замкненої обмеженої множина з простору ). Будь-яка замкнена обмежена множина є або сегментом , або одержується з найменшого сегмента , що містить замкнену множину , вилученням скінченної або зчисленної множини попарно неперетинних інтервалів , кінці яких належать множині . Інтервали називаються доповняльними множини .

Доведення. Якщо є сегмент, то все очевидно. Нехай . Розглянемо . Очевидно, що . Оскільки точки , то . Отже множина є відкритою і за теоремою 2.1.3 ії можно зобразити у вигляді не більш ніж зчисленної множини попарно неперетинних інтервалів. Тоді .

Теорема доведена.

Із означень досконалої множини і ізольованої точки внаслідок теореми 2.1.4 очевидно випливає наступне твердження.

Теорема 2.1.5 Для того щоб замкнена обмежена множина була досконалою необхідно і досить, щоб точки не були кінцями інтервалів і будь-які доповняльні інтервали не мали спільних кінців.

Канторова відкрита множина, Канторова досконала множина

Трійковим дробом називається сума ряду , де або 1, або 2. Цей ряд збігається, сума його невід’ємна і не перевищує одиниці, тому що члени його мажоруються членами геометричної прогресії. Трійковий дріб будемо зображати символом і також називати трійковим дробом. Трійковий дріб виду , де , називається трійково-раціональним числом. Ця сума дорівнює раціональному числу , де ціле число менше за . Трійково-раціональне число , де , крім зображення (запис (0) («0 в періоді») означає, що усі якщо ) має зображення (запис (2) («2 в періоді») означає, що усі якщо ). Має місце наступне твердження.

Теорема 2.1.6 Будь-яке число можливо зобразити трійковим дробом. При цьому зображення єдине, якщо не є трійково-раціональним числом.

Доведення теореми 2.1.6 аналогічне доведенню теореми 1.4.2.

Далі розглянемо наступні інтервали. Нехай є інтервал (0,1; 0,1(2)) і для кожного k=1,2,… розглянемо інтервалів де або 2. Довжина кожного з них дорівнює . Очевидно, що інтервали можливо зобразити у вигляду .

Лема 2.1.1. Різним наборам чисел відповідають різні інтервали . Крім того вони не перетинаються, не мають спільних кінців і, очевидно, що точки 0 і 1 не є кінцями ціх інтервалів.

Дійсно, нехай , де і довільні. Покажемо, що лівий кінець інтервала більше правого

кінця інтервалу:

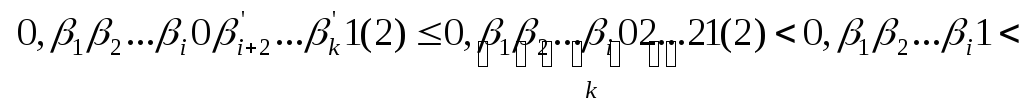
Із означень інтервалів випливає, що точки 0 і 1 не є кінцями ціх інтервалів.

Арифметична характеристика чисел, які належать інтервалам .

Лема 2.1.2. Для того, щоб необхідно і достатньо, щоб число в трійковому запису мало вигляд , де або 2, а довільні і хоча б одно з них не дорівнює нулю і хоча б одно з них не дорівнює 2.

Достатність. Нехай число в трійковому запису має вигляд , де або 2, а довільні і хоча б одно з них не дорівнює нулю і хоча б одно з них не дорівнює 2. Тоді:

.

Необхідність. Якщо , то повинно бути більше за лівий кінець інтервалу , тобто , де хоча б одна з цифр не дорівнює нулю (тому що у протилежному випадку збігається з лівим кінцем інтервалу і отже не належить йому), а з іншого боку повинно бути менше за правий кінець інтервалу , тобто , де хоча б одна з цифр не дорівнює двом, тому що у протилежному випадку збігається з правим кінцем інтервалу і тому не належить йому. Лему доведено.

Побудова Канторових множин.

Поступимо наступним чином: вилучимо з сегмента спочатку інтервал , потім два інтервалу , на му кроці вилучимо інтервалів . Об’єднання усіх інтервалів називається Канторовою відкритою множиною і позначається через , а доповнення множини до сегмента називається Канторовою досконалою множиною і позначається через . За лемою 2.1.2 Канторова відкрита множина це множина усіх чисел з сегмента , трійковий запис яких неможливий без цифри 1. Наприклад, число (в трійковому запису) 0,1 має також вигляд 0,0(2), а тому воно не належить множині . Канторова досконала множина дійсно досконала тому, що одержується з сегмента вилученням зчисленної множина інтервалів , що не мають спільних кінців і точки 0 і 1 не є кінцями ціх інтервалів. З арифметичної характеристики множини випливає, що Канторова досконала множина це множина усіх чисел сегмента , трійковий запис яких містить тільки цифри 0 і 2, тобто це множина усіх трійкових дробів вигляду , де або 2, отже це множина потужності континууму. Обчислимо суму довжин вилучених інтервалів: Спочатку вилучається інтервал , довжина якого дорівнює , потім два інтервала, довжина кожного з яких дорівнює , на му кроці вилучається інтервалів , довжина кожного з яких дорівнює . Отже, сума довжин вилучених інтервалів дорівнює

Означення 2.1.5 Сім’я відкритих множин називається покриттям множини , якщо

Лема 2.1.3. (Гейне-Бореля). Із будь-якого покриття замкненої обмеженої множини відкритими множинами можна виділити скінченнне покриття.

Доведення. Припустимо, що лема не має місце. Так як множина обмежена, то знайдеться сегмент , що містить множину . Нехай . Тоді хоча б для одної з замкнених множин або не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через , а сегмент, в якому вона міститься через . Очевидно, що і довжина сегмента у два рази менша довжини сегмент :=1/2. Нехай побудована послідовність вкладених сегментів таких, що для множин неможливо вилучити скінченнне покриття, , а також =. Нехай . Тоді хоча б для одної з замкнених множин або не існує скінченнного покриття. Позначимо цю множину, або одну з них, якщо їх дві, через , а сегмент, в якому вона міститься через .

Внаслідок принципу математичної індукції існують послідовність вкладених сегментів , довжини яких прямують до нуля, і послідовність вкладених замкнених множин , таких, що для кожної з них неможливо вилучити скінченнне покриття.

За теоремою про послідовніть вкладених сегментів існує єдина спільна точка . Тоді точка є граничною точкою замкненої множини і, отже належить до неї. Нехай  відкрита множина з даного покриття, що містить точку , і . Якщо таке, що , то усі сегменти за умовою, що . Отже всі множини покриваються відкритою множиною за умовою, що , а це суперечить властивостям множин . Одержана суперечність спростовує припущення. Лема доведена.

Зауваження. Лема Гейне-Бореля має місце і в просторі .