3.1. Зчислені множини та їх властивості

Означення 1.3.1. Множини А називається зчисленною, або множиною зчисленної потужності, якщо вона еквівалентна множині натуральних чисел . Зчисленну потужність множини будемо позначати літерою . Тобто запис означає, що множини А зчисленна.

Теорема 1.3.1 (Критерій зчисленості множини). Щоб множина А була зчисленною, необхідно і досить, щоб її можно було зображити у вигляді послідовності:

Доведення. Необхідність. Нехай . Елемент множини , що відповідає натуральному числу позначимо через . Тим самим визначено загальний член послідовності. Отже :

Достатність. Нехай де всі елементи послідовності різні. Кожному елементу поставимо у відповідність його номер . Оскільки різні елементи мають різні номери і кожне натуральне число відповідає елементу , то множина .

Загальні властивості потужності множин.

1. Будь яка нескінченна множина А має потужність не меншу зчисленної потужності, тобто .

Доведення. Виберемо будь який елемент в множині А і позначимо його через . Оскільки різниця теж нескінченна, виберемо із неї будь який елемент і позначимо його через . Припустимо, що вже вибрано елементи , , …, . Різниця  нескінченна. Тому із неї можливо вибрати елемент , де m  довільне натуральне число. Отже з множини А виділина підмножина зчисленної потужності. А це означає, що .

2. Об’єднання зчисленної множини і скінченної множини еквівалентно множині А, отже  зчисленна множина.

Доведення. Спочатку в рядок запишемо елементи множини , а потім будемо виписувати елементи множини А , пропускаючи ті елементи, що належать також множині . Множина буде зображена у вигляді послідовності, отже вона скінченна.

3. Об’єднання нескінченної множини А і скінченної або зчисленної множини В еквівалентно множині А.

Доведення. Виділимо з множини зчислену підмножину і нехай D – різниця множин і А . Тоді і . Оскільки  і , то внаслідок властивості 3 еквівалентних множин .

4. Якщо різниця множини і скінченної або зчисленної множини В – нескінченна, то різниця А \ В еквівалентна множині А.

Доведення. Перетин скінченна або зчисленна множина. Отже, за попередньої властивістю внаслідок рівності 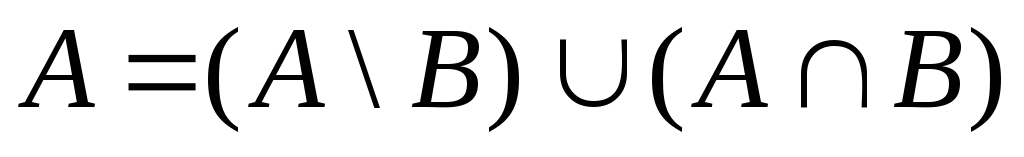одержимо властивість 4.

5. Об’єднання зчисленної множини скінченних множин  зчисленна або скінченна множина.

Доведення. Спочатку в рядок запишемо елементи множини , а потім будемо виписувати елементи множин, пропускаючи ті елементи, що уже вибрані. Множина буде зображена у вигляді рядка або послідовності, отже вона скінченна або зчисленна.

6. Об’єднання скінченної множини зчисленних множин  зчисленна множина.

Доведення. Кожну множину зобразимо у вигляді послідовності , а потім будемо виписувати елементи множин в рядок спочатку з нижнім індексом равним одиниці, потім равним 2 і так далі, пропускаючи ті елементи, що уже вибрані.

7. Об’єднання зчисленної множини зчисленних множин  зчисленна множина.

Доведення. Множину зобразимо у вигляді послідовності . Першим в рядок поставимо елемент, а потім запишемо елементи у яких сума верхнього і нижнього індексів дорівнює трьом, чотирьом і так далі. При цьому будемо виписувати елементи множин , пропускаючи ті елементи, що уже вибрані. Множина буде зображена у вигляді послідовності, отже вона зчисленна.

8. Якщо елементи множини А визначаються m значками, тобто , кожен з яких приймає зчисленну кількість значень , то А  зчисленна.

Доведення. Застосуємо метод математично індукції. Якщо елементи множини визначаються одним значком, значення якого , то множину А можливо зобразити у вигляді 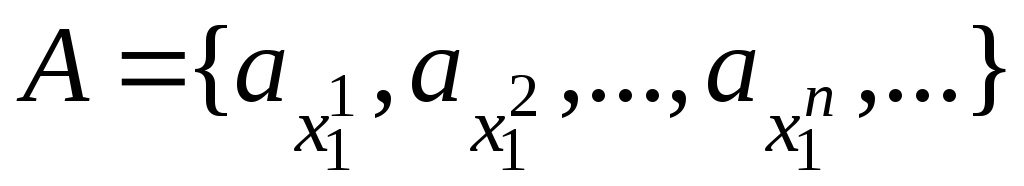. Отже А  зчисленна. Нехай властивість 8 має місце для k індексів (). Розглянемо множину і її підмножину елементів, у яких k+1 індекс має фіксоване довільне значення . В силу припущення, кожна множина  зчисленна, а тоді зчисленна множина А тому, що . Отже, за принципом математичної індукції властивість 8 має місце для будь якого m.

Приклади зчисленних множин.

1. Множина  усіх натуральних чисел зчисленна, тому що .

2. Будь-яка нескінченна підмножина натуральних чисел зчисленна, тому що її можливо зобразити у вигляді .

3. Множина усіх додатних раціональних чисел зчисленна. можливо зобразити у вигляді =, де  множина раціональних чисел вигляду . Оскільки кожна множина  зчисленна, то завдяки властивості 7 множина є зчисленною.

4. Множина усіх від’ємних раціональних чисел зчисленна, оскільки .

5. Множина усіх раціональних чисел зчисленна, завдяки тому, що

6. Множина A={ усіх точек к-вимірного евклідового простору , координати яких раціональні числа,  зчисленна.

Дійсно елементи множини A визначаються значками (координатами точки), кожен з яких приймає зчисленну множину значень. Отже, внаслідок властивості 8, множина A  зчисленна.

7. Множина всіх алгебраїчних многочленів степеня не вище n з раціональними коефіцієнтами зчисленна.

Дійсно кожен елемент множини визначається раціональними коефіцієнтами: . Отже, завдяки властивості 8, множина  зчисленна.

8. Множина всіх алгебраїчних многочленів з раціональними коефіцієнтами зчисленна.

Множину можливо зобразити у вигляді . Тому, завдяки властивості 7, множина  зчисленна.

9. Множина всіх алгебраїчних чисел  зчисленна.

Позначимо через множину алгебраїчних чисел, що відповідають алгебраїчному многочлену з раціональними коефіцієнтами, тобто множину розв’язків рівняння = 0. Множина для кожного многочлена має не більше n елементів. Оскільки , то внаслідок властивості 5,  скінченна або зчисленна. Але множина не може бути скінченною, бо вона містить усі раціональні числа.