5.5. Інтеграл Лебега по множені нескінченної міри
Означення
5.5.1. Нехай
вимірна
множина нескінченної міри, наприклад,
множина усіх дійсних чисел
,
або проміні
.
Послідовність
вимірних обмежених множин називається
вичерпною, якщо вона монотонно зростає,
тобто
,
і
.
Означення
5.5.2.
Вимірна функція
,
що задана на вимірній множині
нескінченної міри, називається інтегровною
за Лебегом на множині
,
якщо для довільної вичерпної послідовності
множин
існує скінченна границя
,
(5.5.1)
яка не
залежить від вибору послідовності
множин
.
Інтегралом від функції
називається
(5.5.2)
Покажемо,
що границя (5.5.2) існує і скінченна, якщо
виконується (5.5.1). Нехай
,
тоді
,
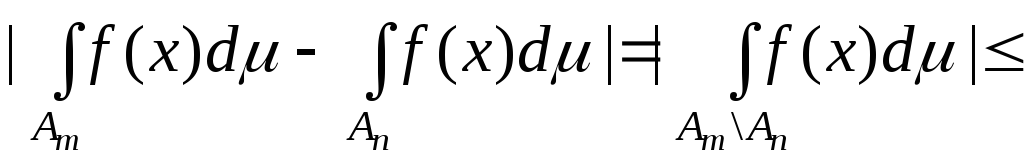
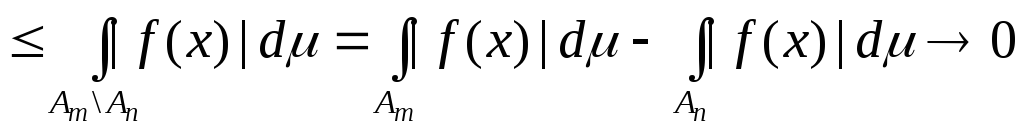коли
.
Теорема
5.5.1.
Якщо
існує невласний інтеграл Рімана від
функції
,
що задана на осі, або проміні, то існує
інтеграл Лебега і вони збігаються.
Доведення.
Розглянемо випадок, коли функція
визначена на осі, інший випадок
аналогічний. Нехай існує невласний
інтеграл Рімана
і
довільна вичерпна послідовність множин.
Для довільного числа
знайдеться число
таке, що
.
(5.5.3)
Введемо
множини
.
Послідовність множин
не спадає і
.
На підставі властивості 11 вимірних
множин
.
Тоді знайдеться натуральне число
таке,
що для усіх
виконується нерівність
,
де число
,
у відповідності з абсолютно неперервністю
інтеграла Лебега, вибрано так, для що
,
міра якої
,
має місце нерівність
.
(5.5.4)
Із
(5.5.3) – (5.5.4) для усіх
випливають нерівності
.
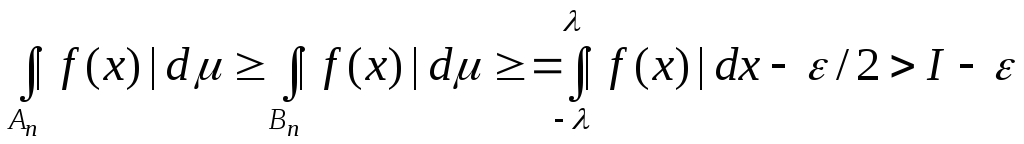(5.5.5)
З іншого
боку, нехай
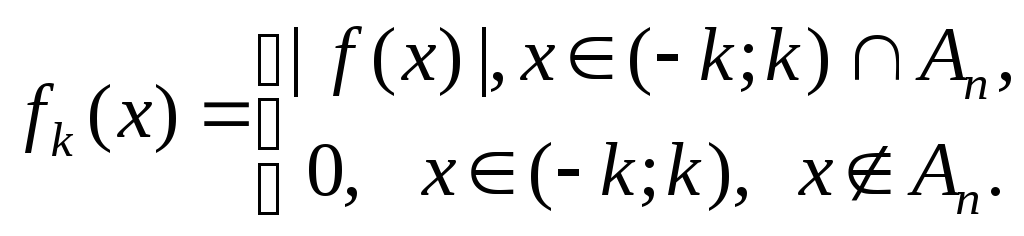
Послідовність
функцій
монотонна, збігається у кожній точці
до
функції
,
отже на підставі теореми Лебега про
граничний перехід під знаком інтеграла,
маємо
(5.5.6)
Із
нерівностей (5.5.5) – (5.5.6) слідує існування
скінченної границі (5.5.1) і рівність
.
Нехай
,
де
довільна вичерпна послідовність.
Очевидно, що існують скінченні границі
і тоді
.
Теорема доведена.
Зауваження
5.5.1. Із
доведення теореми 5.5.1 випливає, що в
означенні 5.5.2, у випадку інтегрованості
функції на осі, або проміні, достатньо
брати вичерпну послідовність множин
.