5.4 Порівняння інтегралів Рімана і Лебега

Нехай обмежена функція, визначена на сегменті , тобто

, (5.4.1)

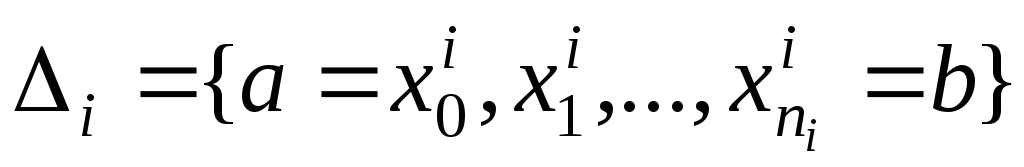
і  послідовність наборів точок сегменту таких, що. Покладемо , і визначимо дві послідовності простих функцій:

, . Із означення функцій , і (5.4.1) випливає

. (5.4.2)

Отже, функції ,  прості і обмежені і слід інтегровні за Лебегом:

, ,

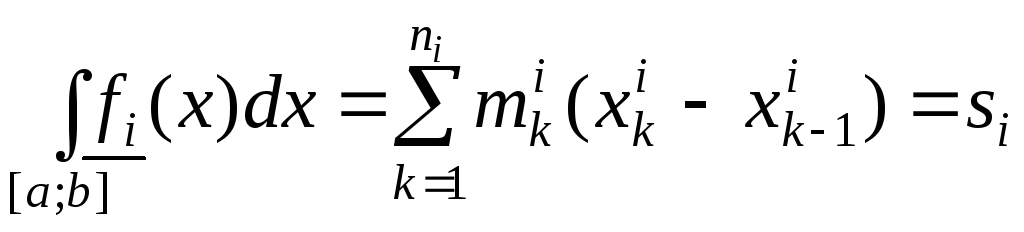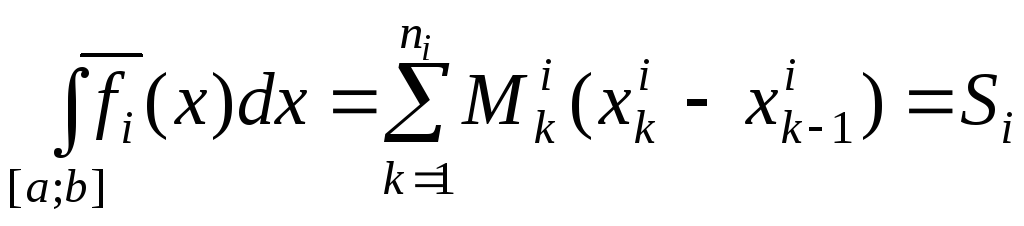де відповідно нижня і верхня суми Дарбу функції . Оскільки при умові виконуються нерівності , то послідовність функцій не спадає, а послідовність функцій не зростає. Отже для послідовностей функцій і виконуються умови теореми Леві, за якою існують майже скрізь границі і , функції і інтегровні за Лебегом на сегменті і

, (5.4.3)

. (5.4.4)

Окрім того, із нерівностей (5.4.2) випливає, що для функцій і мають місце нерівності

. (5.4.5)

Із (5.4.3) – (5.4.5) одержимо

. (5.4.6)

Теорема 5.4.1 Для того щоб функція була інтегровною за Ріманом необхідно і досить, щоб майже скрізь на сегменті для будь-якої послідовності такої, що , коли і в цьому випадку функція інтегровна за Лебегом і інтеграл Рімана збігається з інтегралом Лебега:

.

Достатність. Нехай . Тоді, внаслідок (5.4.6), інтеграл в (5.4.6) дорівнює нулю і . Отже функція інтегровна за Ріманом.

Необхідність. Нехай функція інтегровна за Ріманом. Тоді для будь-якої послідовності такої, що , права частина в (5.4.6) дорівнює нулю. На підставі наслідку 5.2.2 (з нерівності Чебишева) різниця майже скрізь дорівнює нулю. А тоді із нерівностей (5.4.5) випливає еквівалентність функції функціям і. Отже, функція інтегровна за Лебегом і, в силу (5.4.3) або (5.4.4), інтеграл Рімана збігається з інтегралом Лебега.

Теорема 5.4.2 (Теорема Лебега). Для того щоб обмежена функція була інтегровною за Ріманом на сегменті , необхідно і досить, щоб була майже скрізь неперервною на сегменті .

Достатність. Нехай майже скрізь неперервна на сегменті і множина точок розриву. Візьмемо будь-яку послідовність точок розбиття таку, що і нехай . Множина зчисленна, тому має міру нуль. Покажемо, що у кожній точці має місце рівність . Візьмемо довільне число . Внаслідок неперервності функції в точці існує таке, що , якщо . Оскільки , то знайдеться натуральне число таке, що для усіх сегменти , що містять точку , будуть міститься в інтервалі . Тоді, для усіх різниця , тобто майже скрізь. За теоремою 5.4.1 функція інтегровна за Ріманом.

Необхідність. Нехай функція інтегровна за Ріманом. За теоремою 5.4.1 і, в силу (5.4.5), майже скрізь. Позначимо через множину точок сегмента , де . Візьмемо будь-яку послідовність точок розбиття сегмента таку, що і нехай . Множина має міру нуль. Покажемо, що у кожній точці функція неперервна. Візьмемо довільне число . В силу збіжності послідовностей функцій і відповідно до функцій і знайдеться натуральне число таке, що для усіх виконуються нерівності

,

із яких випливає нерівність

(5.4.7)

Візьмемо сегмент , що містить точку . Оскільки не є точкою розбиття, то знайдеться інтервал , що міститься у сегменті . Із означення функцій , і нерівності (5.4.7) маємо

для будь-якого .

Теорема доведена.