4.2.1 Приклади вимірних функцій

1. Функція  вимірна.

Дійсно

2. Функція називається простою, якщо множину можливо зобразити у вигляді об’єднання скінченної або зчисленної множини вимірних попарно неперетинних множин таких, що.

Будь-яка проста функція вимірна. Це випливає із вимірності функції на кожній множині і з рівності .

3. Функція , що визначена і неперервна на сегменті , є вимірною. В даному прикладі .

Покажемо, що множина замкнена для будь-якого . Нехай гранична точка множини . Тоді існує послідовність така, що коли. Спрямувавши до нескінченності, з нерівності і неперервності функції , одержимо . Отже множина замкнена і тому є вимірною. Завдяки критерію вимірності функція є вимірною.

4.3.1. Загальні властивості вимірних функцій

1. Будь- яка функція, що визначена на множині міри нуль, вимірна.

Дійсно, в цьому випадку множина для будь-якого є підмножиною множини міри нуль, отже і сама є множиною міри нуль.

2. Якщо функція вимірна на множині , то функція вимірна.

Для будь-якого розглянемо множину

Оскільки множина розв’язків нерівностей збігається з перетином і отже вимірна, тому вимірна.

Зауваження. Якщо функція вимірна на множині , то функція може бути невимірною на множині , якщо .

Дійсно, якщо , то існує невимірна підмножина множини . Розглянемо функцію

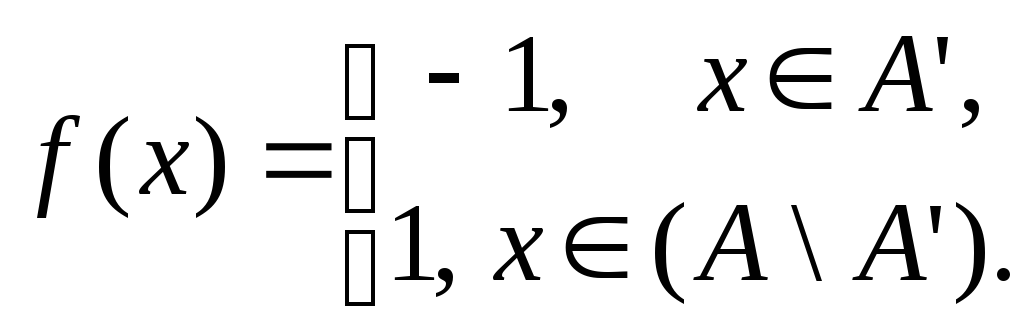
Очевидно, що , отже вимірна. Проте , отже невимірна.

3. Якщо функція вимірна на множині , то функція вимірна.

Для будь-якого множина

Множина розв’язків нерівностей збігається з перетином і отже вимірна, тому функція вимірна.

4. Нехай множина є об’єднання скінченної або зчисленної множини вимірних множин , на яких функція вимірна. Тоді функція вимірна на множині . Ця властивість випливає з наступної рівності.

.

5. Якщо функції і вимірні на множині , то множина вимірна.

Доведення. Нехай множина усіх раціональних чисел. Доведемо рівність

.

Нехай , тобто . Існує раціональне число таке, що , отже елемент належить доданку правої частини з номером . Якщо елемент належить деякому доданку правої частини з номером , то виконуються нерівності , отже . Оскільки кожна множина вимірна, то об’єднання цих множин вимірне, отже множина вимірна.

4.4.1. Властивості вимірних функцій пов’язані з алгебраїчними операциями

6. Якщо функція вимірна на множині , то для будь-якої константи  функція вимірна.

Властивість випливає з рівності .

7. Якщо функція вимірна на множині , то для будь-якої константи  функція вимірна.

Якщо =0, і отже вимірна. Нехай . В цьому випадку вимірність добутку випливає з рівності:

8. Якщо функції і вимірні на множині , то сума і різниця цих функцій вимірні.

Вимірність суми  випливає з властивостей 46 і рівності

.

9. Якщо функції і вимірні на множині , то добуток вимірна функція.

Ця властивість випливає з властивостей 2, 6, 7 і рівності

.

10. Якщо функції вимірна на множині і на множені , то функція  вимірна.

Властивість випливає з рівності

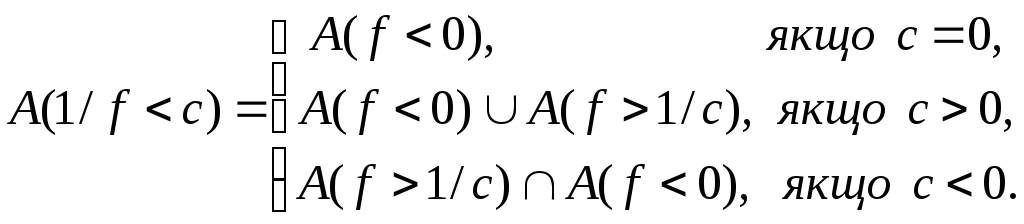
11. Якщо функції і вимірні на множині і на множені , то частка  вимірна функція.

Випливає з властивостей 10 і 9.