Теорія міри та інтеграла лебега

Глава I

ОСНОВИ ТЕОРІЇ МНОЖИН

1.1. Поняття множини, операції над множинами

Означення 1.1.1. Множиною називається сукупність, набір, сім’я, збори, колекція предметів, вибраних по деякому правилу (закону), або просто указаних; при цьому усі предмети різні. Предмети, із яких складається множина називаються елементами.

Множини будемо позначати прописними латинськими буквами, а елементи – малими літерами. Якщо елемент a належить множині A, то це будимо записувати так: а  А.

Приклади.

1. множина усіх натуральних чисел, множина всіх цілих чисел, множина всіх дійсних чисел, множина всіх раціональних чисел.

2. Сегмент множина всіх дійсних чисел , що задовольняють умову , інтервал множина всіх дійсних чисел , що задовольняють умову , півінтервал множина всіх дійсних чисел , що задовольняють умову , півінтервал множина всіх дійсних чисел , що задовольняють умову .

3. множина усіх функцій заданих і неперервних на сегменті , множина всіх функцій заданих і обмежених на сегменті .

Якщо кожен елемент множини А є елементом множини В, то будемо казати, що множина А міститься в множині В, або множина В містить множину А і позначати це будемо так: АВ, або ВА. Будемо також казати, що множина А є підмножиною множини В. Наприклад, , .

Якщо кожен елемент множини А є елементом множини В і навпаки кожен елемент множини В є елементом множини А, то множини рівні: А = В. Отже, щоб довести, що множини А і В рівні треба показати, що А  В і В  А.

Означення 1.1.2. Нехай задана деяка сім’я множин: . Множина всіх елементів, що належать хоч би однієї із множин даної сім’ї, називається об’єднанням множин і позначається об’єднання так .

Якщо маємо дві множини А і В, то їх об’єднання позначимо через . Якщо множин n штук: , то позначення їх об’єднання буде , або .

Означення 1.1.3. Перетином множин сім’я називається множина всіх спільних елементів множин даної сім’ї.

Позначення перетину: перетин сім’ї множин  , перетин двох множин  , перетин n множин  , або . Якщо множини не мають спільних елементів, то будемо казати, що їх перетин – порожня множина. Порожню множину будемо позначати символом . Порожня множина може бути не тільки результатом перетину. Наприклад: множина дійсних розв’язків рівняння – порожня множина.

Означення 1.1.4. Різницею множини А і В називається множина усіх елементів множини А, що не належать множині В. Різниця множин А і В позначається таким чином: А \ В .

Означення 1.1.5. Симетричною різницею множини А і В називається множина 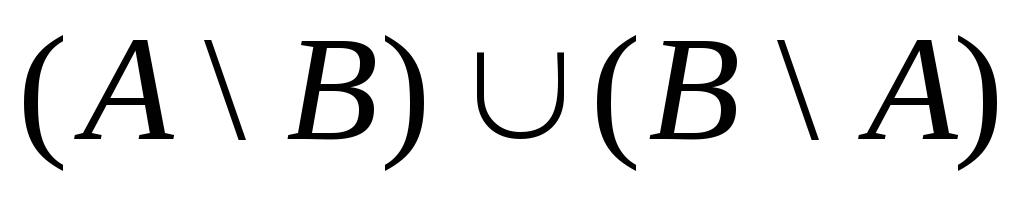. Різниця позначається так: .

Означення 1.1.6. Якщо множина В є підмножиною множини А, то різниця множин А і В називається доповнення множини В до множини А. Доповнення множини В до множини А позначається символом .

Властивості об’єднання, перетину і доповнення множин (властивості двоїстості).

Теорема 1.1.1 (Співвідношення двоїстості). Нехай кожна із множини міститься в множині А. Тоді мають місце рівності:

Доведення. Нехай тобто і , отже для кожного і . Навпаки, нехай , тоді і для кожного . Отже і . Друга рівність доводиться аналогічно.