Тема 1. Элементы линейной алгебры.

Основные теоретические сведения.

1. Определителем (детерминантом) n-го порядка называется число , равное алгебраической сумме n! членов, составленных определенным образом из элементов 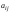определителя. Обозначение:

=det[]=. (1)

Алгебраическим дополнением 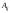элемента определителя n-го порядка называется определитель (n-1)-го порядка, полученный из исходного вычеркиванием i-й строки и j-го столбца и умноженный на .

Рекуррентная формула для вычисления определителя n-го порядка имеет вид

.

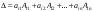(разложение определителя по элементам i-й строки).

Определитель второго порядка

=.

2. Матрицей А=(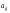) размера называется прямоугольная таблица чисел, состоящая из m строк и n столбцов:

А =.

Произведением матрицы А=() размера 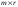на матрицу В=() размера называется матрица С=АВ= размера 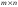с элементами

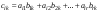(2)

(поэлементное умножение i-й строки матрицы A на k-й столбец матрицы В).

Матрица размера называется квадратной матрицей n-го порядка. Элементы образуют главную диагональ матрицы. Определитель, составленный из элементов квадратной матрицы, называется определителем матрицы и обозначается 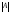или det A.

Матрица Е с элементами = называется единичной матрицей n-го порядка.

Матрица 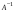называется обратной к матрице А (det A0), если

А=А=Е. (3)

Элементы обратной матрицы А=() вычисляется по формулам

, (4)

где –алгебраическое дополнение элемента 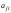, матрицы А, а ее определитель.

3. Матрица называется канонической, если в начале ее главной диагонали стоят единицы, а все остальные элементы равны нулю; например,

.

Любая матрица А может быть приведена к каноническому виду путем элементарных преобразований: а) перестановки столбцов (строк); б) умножение столбца (строки) на число, отличное от нуля; в) прибавление к элементам какого-либо столбца (строки) соответствующих элементов другого столбца (строки), умноженных на число.

Матрицы переходящие друг в друга в результате элементарных преобразований, называются эквивалентными: А~_.

Число r единиц, стоящих на главной диагонали канонической матрицы , не зависит от способа приведения матрицы А к каноническому виду и называется рангом исходной матрицы А: r(A)=r. Эквивалентные матрицы имеют один и тот же ранг.

4. Система трех линейных уравнений с тремя неизвестными x₁, x₂, x₃ имеет вид:

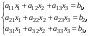(5)

где коэффициенты системы; свободные члены. Определитель третьего порядка , составленный из коэффициентов при неизвестных, называется определителем системы. Если , то единственное решение системы (2) выражается формулами Крамера:

(6)

где определители третьего порядка, получаемые из определителя системы заменой 1, 2 или 3-го столбца соответственно свободными членами

Систему (2) можно записать в матричной форме: АХ=В, где

, ,

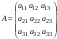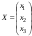Тогда ее решение имеет вид:

, (7)

если определитель системы отличен от нуля.

Если система линейных уравнений с n неизвестными совместна, а ранг матрицы системы меньше числа неизвестных, т.е.

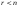, (8)

то система имеет бесконечное множество решений. Свободные n-r неизвестных выбирают произвольно, а главные r неизвестных определяются единственным образом через свободные неизвестные.

5. Вектор столбец:

называется собственным вектором квадратной матрицы го порядка соответствующим собственному значению , если он удовлетворяет матричному уравнению

, или

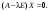
Здесь единичная матрица го порядка, а 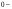нулевой вектор-столбец. При условии, что вектор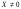, получаем характеристическое уравнение для определения собственных значений :

det (9)

Координаты собственного вектора , соответствующего собственному значению , являются решением системы уравнений

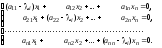(10)

Собственный вектор определяется с точностью до постоянного множителя.

Пример 1. С помощью формул Крамера найти решение системы линейных уравнений:

(11)

Решение. Вычислим определитель системы:

=

Так как 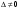, то решение системы может быть найдено по формулам Крамера. (6). Для этого найдем :

,

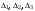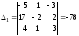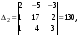
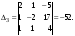
Подставляя найденные значения определителей в формулы (6), получаем искомое решение системы:

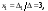
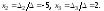
Пример 2. Найти решение системы примера 1 с помощью обратной матрицы.

Решение. Здесь

, ,

Так как определитель матрицы системы отличен от нуля (см. пример 1): 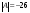, то матрица имеет обратную. Для нахождения обратной матрицы вычислим алгебраические дополнения элементов матрицы :

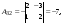
Согласно формуле (2), матрица 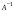, обратная к , имеет вид:

Проверим правильность вычисления , исходя из определения обратной матрицы (3) и используя формулу (2):

Матричное решение системы (11) в силу формулы (7) имеет вид:

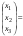
oткуда следует (из условия двух матриц), что

Пример 3. Определить собственные значения и собственные векторы матрицы:

Решение. Характеристическое уравнение для данной матрицы имеет вид:

или

oткуда следует, что матрица имеет два собственных значения и Собственный вектор 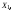соответствующий , определяется из системы уравнений вида:

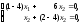или

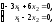
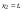которая сводится к одному уравнению . Пологая , получаем решение в виде Следовательно, первый собственный вектор есть

Второй собственной вектор соответствующий собственному значению определяется из системы уравнений вида:

Эта система уравнений также сводится к одному уравнению пологая запишем ее решение в виде . Следовательно, второй собственный вектор есть

Таким образом, матрица имеет два собственных различных значения и и два собственных вектора, равных (с точностью до постоянного множителя) ,