- •Е.А. Матушевская Рабочая тетрадь для лекции 5
- •Тема 5: Экономико-математические методы и модели в экономическом анализе
- •Вопрос 1 Экономико-математические модели : общее понятие и типы
- •Процесс экономико-математического моделирования
- •Вопрос 2 Симплекс-метод: общее понятие и его особенности
- •Вопрос 3 Пример решения задачи оптимизации симплекс-методом
- •Вопрос 4 Понятие экспертных оценок и методы проведения экспертиз
- •Вопрос 5 Расчет коэффициента конкордации и оценка его значимости.
- •Вопрос 6 Пример решения задачи методом экспертных оценок
Вопрос 5 Расчет коэффициента конкордации и оценка его значимости.
Одна из основных целей проведения экспертиз - получение согласованного мнения экспертов. Согласованность оценивается с помощью коэффициентов ранговой корреляции и конкордации.
Коэффициент ранговой корреляции оценивает
Коэффициент конкордации –
Степень согласованности оценок характеризуется коэффициентом конкордации (согласия) W и соответствующим уровнем значимости а.
Коэффициент конкордации определяется по формуле:
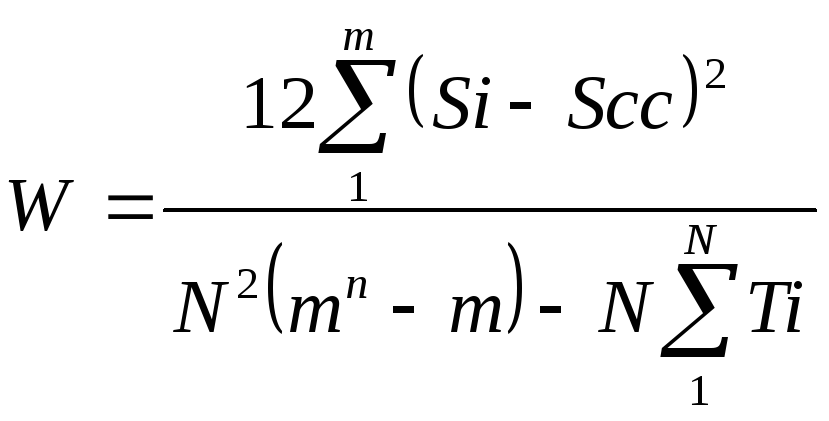 (5.4)
(5.4)
где N - количество экспертов;
m— количество оцениваемых вариантов;
Si - сумма рангов, присвоенных решению Pi всеми экспертами
![]() (5.5)
(5.5)
где Rij- ранг, присвоенный этому решению j экспертом.
Сумма среднеарифметической суммы рангов, полученных всеми объектами, рассчитывается по
формуле:
![]() (5.6)
(5.6)
Показатель, связанных (равных) рангов, назначенных j экспертом, рассчитывается по формуле:
![]() (5.7)
(5.7)
Если все m оценок эксперта различны, то Tj = 0, а если среди рангов есть одинаковые, то Tj
определяется по приведенной формуле.
Если эксперт задал ранги 1, 2, 2, 4, то Tj = 2 - 2 = 6
Во всех случаях показатель степени n равен трем.
Коэффициент конкордации изменяется от 0 до 1.
Обычно согласованность считается удовлетворительной, если W >0,5, если W >0,7, то согласованность считается хорошей.
Величина уровня значимости а определяется с помощью критерия Пирсона с n -1 степенями свободы.
Вопрос 6 Пример решения задачи методом экспертных оценок
Для формирования первоначального набора технико-экономических показателей, влияющих на рост производительности труда машиностроительных и металлообрабатывающих предприятиях Севастополя, работникам отделов труда и заработной платы заводов "Центролит" была роздана анкета. В анкете первого тура указывалось: "В целях изыскания резервов роста производительности труда на Вашем предприятии предлагаем Вам указать по 5 технико-экономических показателей, оказывающих, по Вашему мнению, наибольшее влияние на рост производительности труда". Так как мнения опрашиваемых экспертов-специалистов на совпали полностью, то в первоначальный набор вошли 9 технико-эжкономических показателей работы предприятия:
X1- машиновооруженность рабочих, грн.;
Х2-фондовооруженность рабочих, грн.;
ХЗ- электровооруженность рабочих, кВт.ч;
Х4- энерговооруженность рабочих, Гкал;
Х5 -интегральный коэффициент работы оборудования;
X6- использование баланса рабочего времени ( отработано рабочим чел/дней);
Х7- социально-экономические факторы (разряд, стаж., уровень образования и т.д.);
Х8- условия труда на рабочем месте (освещенность, загазованность, шум, вибрация и т.д.);
Х9- специализация предприятия, коэффициент.
Все они были внесены в анкету второго тура, розданную тем же экспертам-специалистам с предложением проранжировать влияние этих технико-эжкономических показателей на рост производительности труда, (технико-экономическому показателю, оказывающему наибольшее влияние на рост производительности труда присваивается ранг 1, следующему 2, далее 3 и 4 и т. д. (случай несвязанных рангов)). Если же эксперт затрудняется разграничить влияние каких-то показателей на рост производительности труда, то присваивает им одинаковые ранги (случай развитых рангов).
Ответы экспертов сводятся в матрицу рангов, где m - количество экспертов, n- количество технико-экономических показателей-факторов.
Степень согласованности мнений специалистов характеризует коэффициент конкордации W, величина которого изменяется от 0 до 1 (W=0, мнения экспертов не совпадают, W=1, полностью совпадают).
Наличие (отсутствие) связанных рангов обуславливает методику определения коэффициента конкордации, характеризующего степень согласованности мнения экспертов.
При анализе анкет по отдельным заводам имелись случаи наличия связанных (завод "Ценролит") (табл.5.1) рангов в ответах экспертов.
Методика расчета коэффициента конкордации в случае связанных рангов состоит в следующем:
-
Складываются порядковые номера мест факторов.
-
Полученная сумма рангов делится на количество связанных рангов.
-
Каждому связанному фактору присваивается ранг, полученный в результате переранжировки.
4. Последующим факторам присваивается очередной номер, не участвовавший в предыдущих расчетах.
|
Таблица 5.1 - Матрица рангов ответов экспертов литейного завода Ценролит" |
|||||
|
Факторы |
Эксперты |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
XI |
1 |
1 |
1 |
1 |
1 |
|
Х2 |
5 |
4 |
2 |
4 |
4 |
|
ХЗ |
2 |
1 |
2 |
2 |
2 |
|
Х4 |
5 |
4 |
4 |
4 |
4 |
|
Х5 |
4 |
3 |
4 |
3 |
3 |
|
Х6 |
2 |
1 |
1 |
2 |
3 |
|
Х7 |
3 |
2 |
3 |
2 |
2 |
|
Х8 |
3 |
2 |
3 |
2 |
2 |
|
Х9 |
5 |
3 |
4 |
4 |
4 |
|
Сумма |
30 |
21 |
24 |
24 |
25 |
Переранжировка рангов факторов в первом столбце табл.5.1. Ранг фактора Х1=1, ХЗ = Х6=
(2+3)/2=2,5; Х7 - Х8= (4+5) / 2- 4,5; Х5=6; Х2=Х4- Х9 - (7+8+9 /3 = 8.
В остальных столбцах переранжировки рангов факторов осуществляются аналогично.
Результаты переранжировки сводятся в матрицу переранжировки рангов (табл.5.2).
|
Таблица 5.2 -Матрица переранжировки рангов |
||||||||
|
Факторы |
Эксперты |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
XI |
1 |
2 |
1,5 |
1 |
1 |
6,5 |
-18,5 |
342,25 |
|
Х2 |
8 |
8,5 |
3,5 |
8 |
8 |
36 |
+11 |
121 |
|
хз |
2,5 |
2 |
3,5 |
3,5 |
4,5 |
14,5 |
-10,5 |
110,25 |
|
Х4 |
8 |
8,5 |
8 |
8 |
8 |
40,5 |
+15,5 |
240,25 |
|
Х5 |
6 |
6,5 |
8 |
6 |
5,5 |
32 |
+7 |
49 |
|
Х6 |
2,5 |
2 |
1,5 |
3,5 |
5,5 |
15 |
-10 |
100 |
|
Х7 |
4,5 |
4,5 |
5,5 |
3,5 |
3 |
21 |
-4 |
16 |
|
Х8 |
4,5 |
4,5 |
5,5 |
3,5 |
3 |
21 |
-4 |
16 |
|
Х9 |
8 |
6,5 |
8 |
8 |
8 |
38,5 |
+13,5 |
182,25 |
|
I |
45 |
45 |
45 |
45 |
45 |
368 |
|
1177 |
-
Суммы рангов столбцов после переранжировки должны быть равны между собой -45.
-
По дочитываются суммы рангов каждой в отдельности взятой строки и всех строк.
-
Сумма рангов столбцов должна быть равна сумме рангов строк-225 (графа 7, табл.5.2).
-
Определяется средний ранг фактора.
![]()
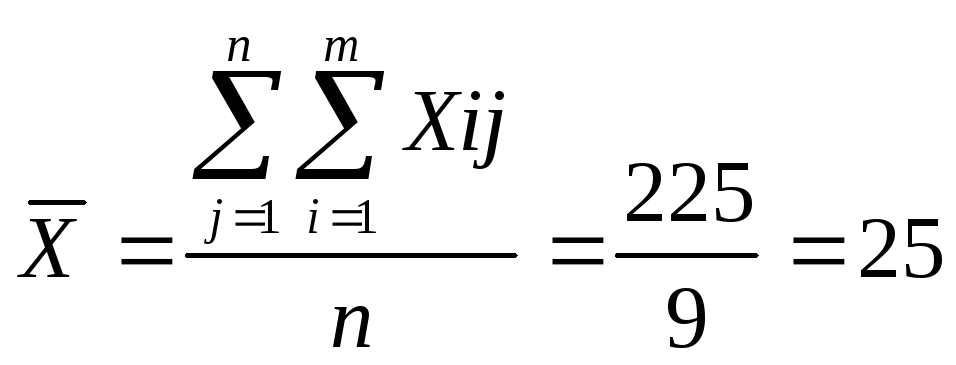
1. Определяется величина 5 (графа 9, табл.5.2).
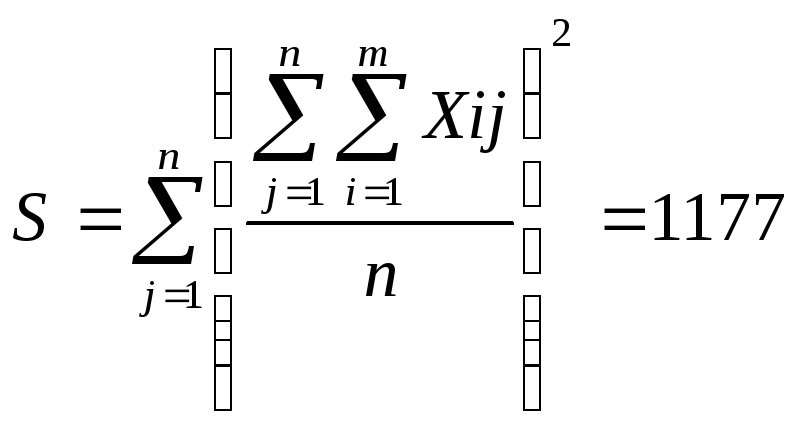
Формула коэффициента конкордации имеет вид:
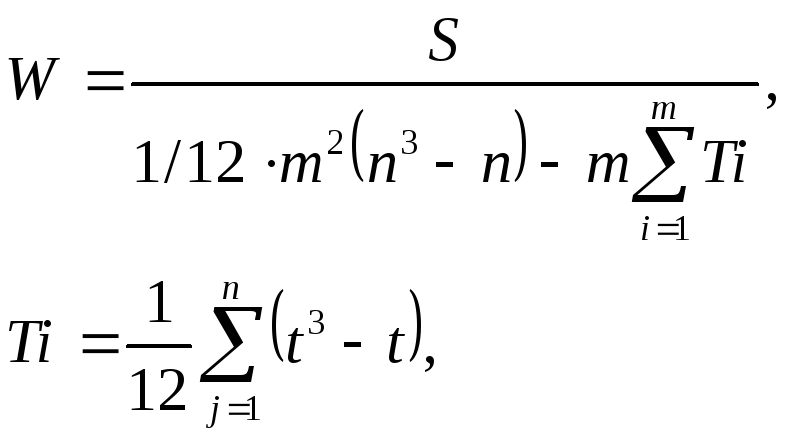
Где t -число связанных рангов в каждом отдельно взятом столбце матрицы рангов. Т1 = 1/12 *[(23-2) +(23 -2)+(33-3)]=3,
………………………………………..
Т5 = 1/12 * [ (33 -3) + (23 -2) +(33 - 3)]=4,5
1. и-
Ti=3+3,5+3,5+7+4,5-21,5
![]()
Для
определения значимости коэффициента
конкордации исчисляется критерий
![]() 2
(Пирсона)
с числом степеней
свободы n-1.
2
(Пирсона)
с числом степеней
свободы n-1.
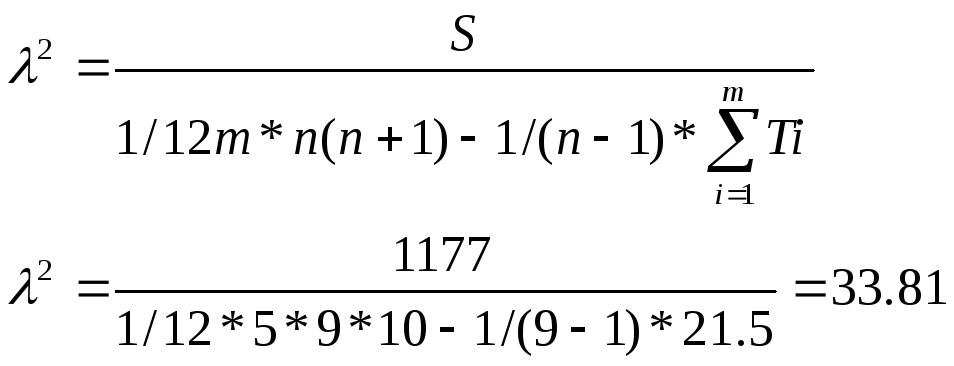
Значение
![]() 2
сравнивается с
табличным
2
сравнивается с
табличным
![]() 2Т.
Величина
2Т.
Величина
![]() 2
должна быть больше
2
должна быть больше
![]() 2Т,
так как
2Т,
так как
![]()
 2>
2>![]() 2т,
при
5 %-ном уровне значимости, то нулевую
гипотезу случайности совпадений мнений
экспертов
следует считать отвергнутой. [Борщевский
и. И., Трухов В. А. Производительность
труда:
Методы анализа и прогнозирования / Под
ред. А. А. Ракова: Наука и техника. ]
2т,
при
5 %-ном уровне значимости, то нулевую
гипотезу случайности совпадений мнений
экспертов
следует считать отвергнутой. [Борщевский
и. И., Трухов В. А. Производительность
труда:
Методы анализа и прогнозирования / Под
ред. А. А. Ракова: Наука и техника. ]
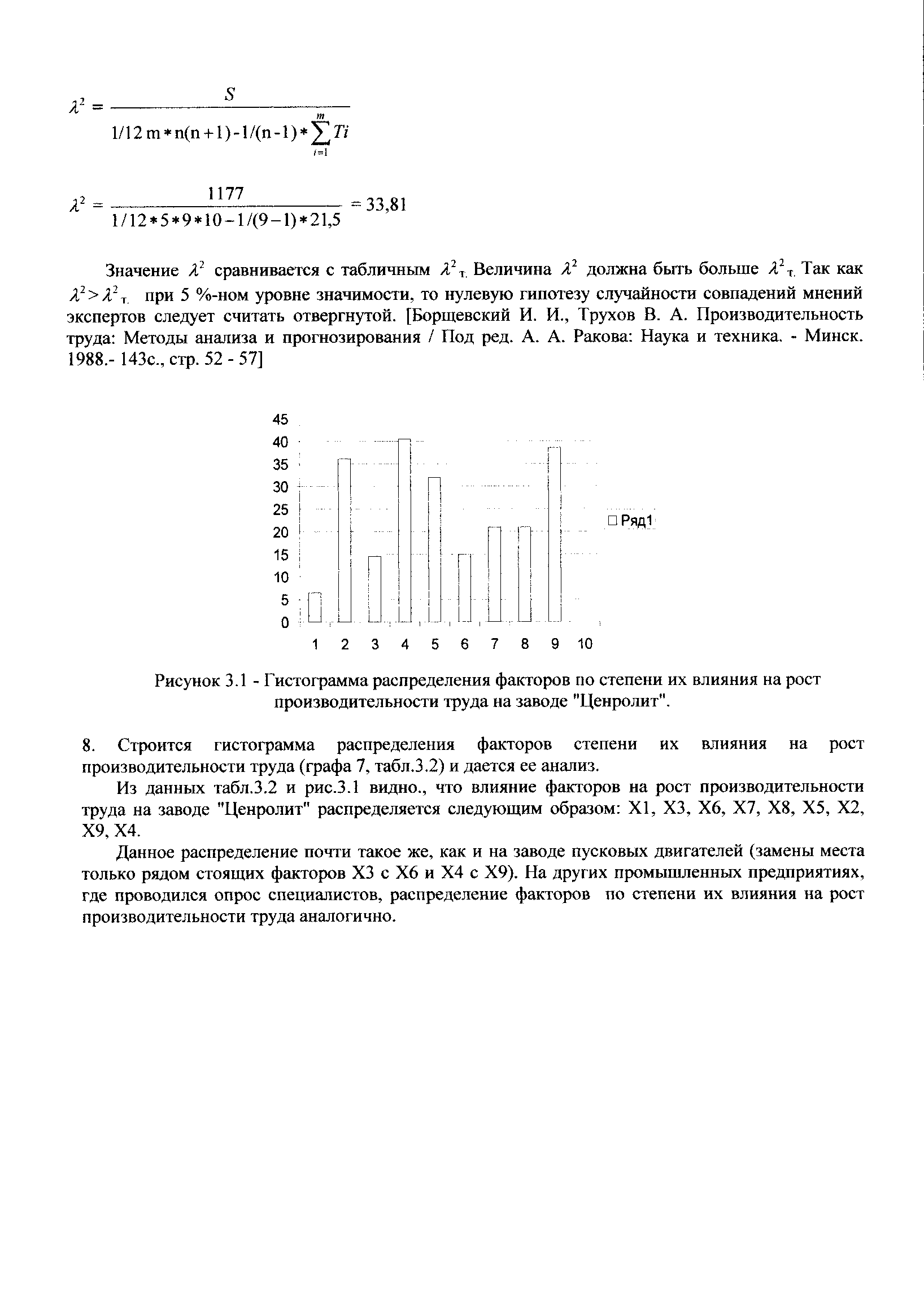
Рисунок 5.1 - Гистограмма распределения факторов по степени их влияния на рост производительности труда на заводе "Ценролит".
8. Строится гистограмма распределения факторов степени производительности труда (графа 7, табл.5.2) и дается ее анализ.
Из данных табл. 5.2 и рис.5.1 видно, что влияние факторов на рост производительности труда на заводе "Ценролит" распределяется следующим образом: XI, ХЗ, Х6, Х7, Х8, Х5, Х2, Х9, Х4.
Данное распределение почти такое же, как и на заводе пусковых двигателей (замены места только рядом стоящих факторов ХЗ с Х6 и Х4 с Х9). На других промышленных предприятиях, где проводился опрос специалистов, распределение факторов по степени их влияния на рост производительности труда аналогично.
1 В зависимости от вида специальных ограничений различают следующие ЗЛП:
-
каноническая ЗЛП, включающая в качестве ограничений только уравнения, т. е.
![]() ;
;
-
стандартная ЗЛП, включающая в качестве ограничений только неравенства, т. е.
![]()