
- •Определитель іі порядка. Его свойства и вычисления
- •Определитель ііІпорядка. Правила его вычисления
- •Линейные операции над матрицами
- •Матицы: основные определения и свойства
- •Миноры и алгебраические дополнения. Обратная матрица
- •Решение системы линейных уравнений по формулам Крамера
- •Решение системы линейных уравнений матричным методом
- •Системы линейных уравнений. Основные определения
- •Решение системы линейных уравнений методом Гауса
- •Декартовые прямоугольные координаты вектора. Орты вектора
- •Скалярные и векторные величины. Линейные операции над векторами
- •Смешанное произведение векторов. Условие компланарности трех векторов
- •Проекция вектора на ось и ее свойства
- •Векторное произведение векторов и его свойства
- •Скалярное произведение векторов и его свойства. Условия колиниарности и ортогональности двух векторов
- •Простейшие задачи аналитической геометрии на плоскости
- •Полярные координаты. Преобразования прямоугольных координат. Уравнение линии на плоскости
- •Уравнение прямой на плоскости (общее и с угловым коэффициентом)
- •Уравнение прямой на плоскости (прямая с угловым коэффициентом, которая проходит через данную точку; прямая, которая проходит через две данные точки)
- •Угол между двумя прямыми на плоскости. Условие их параллельности и перпендикулярности
- •Кривая второго порядка – эллипс. Основные характеристики
- •Кривая второго порядка – гипербола. Основные характеристики
- •Кривая второго порядка – парабола. Основные характеристики
- •Уравнение плоскости. Расстояние от точки к плоскости
- •Угол между двумя плоскостями. Условия их параллельности и перпендикулярности
- •Уравнение прямой в пространстве. Переход от общего уравнения прямой к каноническому
- •Угол между двумя прямыми в пространстве. Условия их параллельности и перпендикулярности
- •Прямая и плоскость в пространстве. Угол между прямой и плоскостью. Условия их параллельности и перпендикулярности
-
Кривая второго порядка – парабола. Основные характеристики
Параболой называется множество точек плоскости в каждой из которых находится на одинаковом расстоянии от данной точки (фокуса) и данной прямой (директрисой).
Начало координат делит пополам отрезок от директрисы до фокуса и этот отрезок (половина) р- параметр параболы.







 каноническое
уравнение параболы
каноническое
уравнение параболы
 фокальный
радиус
фокальный
радиус
Точка пересечения параболы с осью симметрии называется вершиной параболы.
-
Уравнение плоскости. Расстояние от точки к плоскости
 нормальное
уравнение плоскости в векторной форме
нормальное
уравнение плоскости в векторной форме
 общее
уравнение плоскости в векторном виде
общее
уравнение плоскости в векторном виде
 общее
уравнение плоскости в координатной
форме
общее
уравнение плоскости в координатной
форме
 уравнение
связки плоскостей в векторной форме
уравнение
связки плоскостей в векторной форме

Уравнение связки плоскостей в координатной форме
 уравнение
плоскости проходящей через 3 точки в
векторной форме
уравнение
плоскости проходящей через 3 точки в
векторной форме
 уравнение
плоскости проходящей через 3 точки в
координатной форме
уравнение
плоскости проходящей через 3 точки в
координатной форме
 расстояние
от точки к плоскости
расстояние
от точки к плоскости
-
Угол между двумя плоскостями. Условия их параллельности и перпендикулярности
 угол
между плоскостями в векторной форме
угол
между плоскостями в векторной форме
 угол
между плоскостями в координатной форме
угол
между плоскостями в координатной форме
 условие
параллельности плоскостей
условие
параллельности плоскостей
 условие
перпендикулярности плоскостей
условие
перпендикулярности плоскостей
-
Уравнение прямой в пространстве. Переход от общего уравнения прямой к каноническому
 параметрическое
уравнение прямой в векторной форме,
где t
– параметр
параметрическое
уравнение прямой в векторной форме,
где t
– параметр
 параметрическое
уравнение прямой в координатной форме
параметрическое
уравнение прямой в координатной форме
 каноническое
уравнение прямой
каноническое
уравнение прямой
 уравнение
прямой проходящей через две точки
уравнение
прямой проходящей через две точки
 общее
уравнение прямой в векторной форме
общее
уравнение прямой в векторной форме


 общее
уравнение прямой в координатной форме
общее
уравнение прямой в координатной форме
При переходе от общего уравнения к каноническому виду надо найти какую-либо точку принадлежащую прямой и вместо коэффициентов m и nподставить пропорциональные им числа.
-
Угол между двумя прямыми в пространстве. Условия их параллельности и перпендикулярности
 угол
между прямыми в векторной форме
угол
между прямыми в векторной форме
 угол
между прямыми в координатной форме
угол
между прямыми в координатной форме
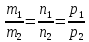 условие
параллельности двух прямых в пространстве
условие
параллельности двух прямых в пространстве
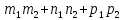 условие
перпендикулярности двух прямых в
пространстве
условие
перпендикулярности двух прямых в
пространстве
-
Прямая и плоскость в пространстве. Угол между прямой и плоскостью. Условия их параллельности и перпендикулярности
Угол между прямой и плоскостью называется любой из двух смежных углов образованных прямой.
 угол
между прямой и плоскостью в пространстве
в векторной форме
угол
между прямой и плоскостью в пространстве
в векторной форме
 угол
между прямой и плоскостью в координатной
форме
угол
между прямой и плоскостью в координатной
форме
 условие
параллельности прямой и плоскости
условие
параллельности прямой и плоскости
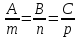 условие
перпендикулярности прямой и плоскости
условие
перпендикулярности прямой и плоскости
