
- •Определитель іі порядка. Его свойства и вычисления
- •Определитель ііІпорядка. Правила его вычисления
- •Линейные операции над матрицами
- •Матицы: основные определения и свойства
- •Миноры и алгебраические дополнения. Обратная матрица
- •Решение системы линейных уравнений по формулам Крамера
- •Решение системы линейных уравнений матричным методом
- •Системы линейных уравнений. Основные определения
- •Решение системы линейных уравнений методом Гауса
- •Декартовые прямоугольные координаты вектора. Орты вектора
- •Скалярные и векторные величины. Линейные операции над векторами
- •Смешанное произведение векторов. Условие компланарности трех векторов
- •Проекция вектора на ось и ее свойства
- •Векторное произведение векторов и его свойства
- •Скалярное произведение векторов и его свойства. Условия колиниарности и ортогональности двух векторов
- •Простейшие задачи аналитической геометрии на плоскости
- •Полярные координаты. Преобразования прямоугольных координат. Уравнение линии на плоскости
- •Уравнение прямой на плоскости (общее и с угловым коэффициентом)
- •Уравнение прямой на плоскости (прямая с угловым коэффициентом, которая проходит через данную точку; прямая, которая проходит через две данные точки)
- •Угол между двумя прямыми на плоскости. Условие их параллельности и перпендикулярности
- •Кривая второго порядка – эллипс. Основные характеристики
- •Кривая второго порядка – гипербола. Основные характеристики
- •Кривая второго порядка – парабола. Основные характеристики
- •Уравнение плоскости. Расстояние от точки к плоскости
- •Угол между двумя плоскостями. Условия их параллельности и перпендикулярности
- •Уравнение прямой в пространстве. Переход от общего уравнения прямой к каноническому
- •Угол между двумя прямыми в пространстве. Условия их параллельности и перпендикулярности
- •Прямая и плоскость в пространстве. Угол между прямой и плоскостью. Условия их параллельности и перпендикулярности
-
Скалярное произведение векторов и его свойства. Условия колиниарности и ортогональности двух векторов
Скалярным
произведением двух не нулевых векторов
 называется число равное произведению
длин этих векторов на косинус угла
между ними.
называется число равное произведению
длин этих векторов на косинус угла
между ними.
Скалярное произведение равно 0 если хотя бы один из векторов равен 0.
( ,
если
,
если
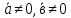
(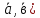 =0,
если
=0,
если
 или
или

Скалярным
квадратом
 называется скалярное произведение
называется скалярное произведение
 .
.
Геометрические свойства скалярного произведения:
-
Косинус угла
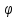 между двумя не нулевыми векторами
определяется по формуле:
между двумя не нулевыми векторами
определяется по формуле:

-
Скалярное произведение обращается в ноль тогда и только тогда когда вектора
 перпендикулярны. (
перпендикулярны. (
-
Скалярное произведение положительно тогда и только тогда когда угол между векторами острый, и отрицательно когда угол тупой.
-
Скалярный квадрат равен квадрату модуля этого вектора.
-
Длинна вектора равен корню квадратному из его скалярного квадрата.

Алгебраические свойства скалярного произведения
-
(

-
(

-
(

-

Необходимое и достаточное условие коллинеарности двух векторов: 2 вектора коллинеарны тогда и только тогда, когда их смешенное произведение равно 0.
![]() или
или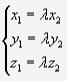
Необходимое и достаточное условие ортогональности двух векторов: « вектора ортогональны тогда и только тогда, когда их скалярное произведение равно 0.
![]()
-
Простейшие задачи аналитической геометрии на плоскости
Задача 1
т. М(х;у)
Найти точки симметричные т. М относительно оси абсцисс, оси ординат и начала координат.
Решение:
Обозначим
искомые точки через т.
 ,
т.
,
т.
 ,
т.
,
т.
 .
.
Пусть
т. N
проекция т. М на ось Ох, т.
 -проекция
т.
-проекция
т.
 на
ось Ох, т. L
– проекция т.М на ось Оу, т.
на
ось Ох, т. L
– проекция т.М на ось Оу, т. -
проекция т.
-
проекция т. на
Оу, т.
на
Оу, т.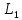 -
проекция т.
-
проекция т.
 на
Оу.
на
Оу.
Рассмотрим
вектора
 и
и






Аналогично
 и
и




Задача 2
Найти
расстояние между двумя данными точками
т. .
.

 -
проекция
-
проекция
 на
ось Ох
на
ось Ох
 -
проекция
-
проекция
 на
ось Оу
на
ось Оу
т.К – пересечение
Рассморим

 К
=
К
=

К =
=
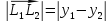
От суда выходит что:
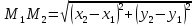 расстояние
между двумя точками
расстояние
между двумя точками
Задача 3
(о делении отрезка в данном отношении)
т.

Дано
число
 - отношение в котором
- отношение в котором
 делит отрезок
делит отрезок
 и определяется по формуле
и определяется по формуле
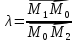
Пусть
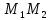 не перпендикулярно оси Ох так как
вектора
не перпендикулярно оси Ох так как
вектора
 параллельны, то выполняется равенство
параллельны, то выполняется равенство

Рассмотрим
вектор
 ;
;
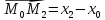
 координаты точки
координаты точки

Частный
случай ( делит
делит
 пополам)
пополам)

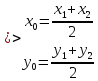
-
Полярные координаты. Преобразования прямоугольных координат. Уравнение линии на плоскости
Возьмем некоторую т.О на плоскости и возьмем прямую ОР.
т.О называется полюсом, а луч с т.О с положительным направлением называется полярной осью. Задание полюса О полярной оси ОР и единичного отрезка ОЕ определяет на плоскости полярную систему координат.
Полярным
радиусом
 т.М называется его расстояние до полюса.
Полярным углом
т.М называется его расстояние до полюса.
Полярным углом
 произвольной т.М называется угол наклона
вектора
произвольной т.М называется угол наклона
вектора
 полярный оси ОР.
полярный оси ОР.
 и
и
 называются полярными координатами
т.М.
называются полярными координатами
т.М.
т.М(
Замечание:
Задание любой пары чисел
 и
и
 ,
,
 позволяет построить на плоскости
единственную т.М для которой данные
числа являются ее полярными координатами.
позволяет построить на плоскости
единственную т.М для которой данные
числа являются ее полярными координатами.
Преобразование декартовых прямоугольных координат
-
Параллельно т.М(

 а
и в задано
а
и в задано

у=
-
Поворот оси
х=
у= +
+
-
Изменение начала и поворот осей
х=
у= +
+
Уравнение линии на плоскости
Рассмотрим соотношение F(x,y)=0 связывающее две переменные х и у. Это уравнение называется уравнением линии L если координаты любой точки линии удовлетворяют это уравнение, а координаты точек не принадлежащие L это уравнение не удовлетворяют.
Таким образом уравнение линии L есть соотношение связывающее координаты точек этой линии.
Например
рассмотрим окружность радиусом
R
с центром в точке
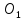 (a,
b).
Эта окружность определяется как
геометрическое место точек находящихся
на расстоянии R
от точки
(a,
b).
Эта окружность определяется как
геометрическое место точек находящихся
на расстоянии R
от точки
 .
.
 уравнение
окружности.
уравнение
окружности.
