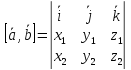7. Скалярные и векторные величины. Линейные операции над векторами

Величины которые определяются только числовым значением называются скалярными. Те которые определяются числовым значением и направлением называются векторными.

Вектором называется направленный отрезок и обозначается .

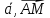Вектор, начло и конец которого совпадают, называется нулевым. Направление такого вектора считается произвольным.

Два не нулевых вектора называются коллинеарными если прямые АВ и СМ параллельны или совпадают

Противоположным для вектора называется вектор той же длинны, но с противоположным направлением.

Длинной (модулем) не нулевого вектора называется расстояние между его началом и концом и обозначается .

Вектор называется свободным если положение их начала не имеет значения.

Свободные векторов называются равными если они коллинеарные, одинаково направлены и имеют одинаковую длину.

Скользящие вектора это вектора которые считаются равными если они имеют равную длину, одинаково направлены и лежат на одной прямой.

Связанные вектора это вектора которые считаются равными если они имеют одинаковую длину, одинаково направлены и имеют одинаковые начала.

Линейные операции над векторами:

Сложение (вычитание) векторов – результатом суммы ( разности) двух векторов является вектор.

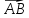Правило треугольника сложения векторов: суммой двух векторов , является вектор идущий из начала в конец .

Правило параллелограмма: суммой двух векторов является вектор 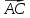определяемый диагональю параллелограмма АВСМ.

Разностью векторов называется вектор для которого исполняется равенство .

Свойства сложения векторов:

• 

• (

• 

• 

15. Смешанное произведение векторов. Условие компланарности трех векторов

Условие компланарности: три вектора компланарны тогда и только тогда когда

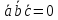
Объем пирамиды построенной на трех векторах вычисляется по формуле:

11. Проекция вектора на ось и ее свойства

Пусть задана ось координат Ох и вектор . Проведем прямые перпендикулярные к оси Ох через точки А и В. Точки пересечения .

Проекцией вектора на ось Ох называется

• длинна вектора если направления вектора и ос Ох совпадают

• минус длинна в противоположном случае -.

Свойства проекции вектора на ось:

• Проекции равных векторов на одну и ту же ось равны между собой.

• При умножении вектора на число его проекция умножается на это же число.

• Проекция суммы вектора на ось равна сумме проекций на эту ось складываемых векторов.

• Проекция вектора на ось Ох равна произведению длинны вектора на косинус угла наклона вектора к оси Ох.

14. Векторное произведение векторов и его свойства

Векторным произведением вектора называется вектор 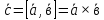такой что:

• Длинна этого вектора равна произведению на где - угол между

• Вектор перпендикулярен каждому из векторов

• Векторы образуют правую тройку векторов

Если вектора коллинеарны, то их векторное произведение называется нулевой вектор.

Свойства векторного произведения:

• При изменении порядка сомножителей векторное произведение меняет знак на противоположный

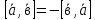
• Векторный квадрат равен нулевому вектору

• Скаляр можно выносить за знак векторного произведения

• 

• Длинна векторного произведения равна площади параллелограмма построенного на данных векторах

• Синус угла между двумя векторами определяется по формуле

Векторное произведение в координатной форме