
- •Определитель іі порядка. Его свойства и вычисления
- •Определитель ііІпорядка. Правила его вычисления
- •Линейные операции над матрицами
- •Матицы: основные определения и свойства
- •Миноры и алгебраические дополнения. Обратная матрица
- •Решение системы линейных уравнений по формулам Крамера
- •Решение системы линейных уравнений матричным методом
- •Системы линейных уравнений. Основные определения
- •Решение системы линейных уравнений методом Гауса
- •Декартовые прямоугольные координаты вектора. Орты вектора
- •Скалярные и векторные величины. Линейные операции над векторами
- •Смешанное произведение векторов. Условие компланарности трех векторов
- •Проекция вектора на ось и ее свойства
- •Векторное произведение векторов и его свойства
- •Скалярное произведение векторов и его свойства. Условия колиниарности и ортогональности двух векторов
- •Простейшие задачи аналитической геометрии на плоскости
- •Полярные координаты. Преобразования прямоугольных координат. Уравнение линии на плоскости
- •Уравнение прямой на плоскости (общее и с угловым коэффициентом)
- •Уравнение прямой на плоскости (прямая с угловым коэффициентом, которая проходит через данную точку; прямая, которая проходит через две данные точки)
- •Угол между двумя прямыми на плоскости. Условие их параллельности и перпендикулярности
- •Кривая второго порядка – эллипс. Основные характеристики
- •Кривая второго порядка – гипербола. Основные характеристики
- •Кривая второго порядка – парабола. Основные характеристики
- •Уравнение плоскости. Расстояние от точки к плоскости
- •Угол между двумя плоскостями. Условия их параллельности и перпендикулярности
- •Уравнение прямой в пространстве. Переход от общего уравнения прямой к каноническому
- •Угол между двумя прямыми в пространстве. Условия их параллельности и перпендикулярности
- •Прямая и плоскость в пространстве. Угол между прямой и плоскостью. Условия их параллельности и перпендикулярности
-
Матицы: основные определения и свойства
Матрицей
называется прямоугольная таблица
чисел, содержащая m
строк одинаковой длины (или у столбцов
одинаковой длины). Матрица записывается
в виде![]() или,
сокращенно A=(aij)
(i=1,m,
j=1,n)
i-номер строки,(т.е.i=1,2,3..m),j-номер столбца.
или,
сокращенно A=(aij)
(i=1,m,
j=1,n)
i-номер строки,(т.е.i=1,2,3..m),j-номер столбца.
Матрицу А называют матрицей размера m x n и пишут Аmxn. Числа aij составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.
Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е. А=В, если aij = bij (i=1,m, j=1,n)
Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера n x n называют матрицей n-го порядка.
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О. В матричном исчислении матрицы О и E играют роль чисел 0 и 1 в арифметике.
Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:
![]()
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается АТ
-
Миноры и алгебраические дополнения. Обратная матрица
Минором любого элемента определителя D называется определитель второго порядка полученный из данного вычеркиванием строки из столбца в котором лежит указанный элемент
D=

Алгебраическим
дополнением любого элемента определителя
D
называется минор этого элемента взяты
со знаком
 ,
где i-
номер строки j
– номер столбца.
,
где i-
номер строки j
– номер столбца.

Обратная
матрица. Для квадратных матриц вводится
понятие обратной матрицы. Если для
матрицы Amxn=(aij) существует
такая матрица
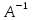 что
что
 где Е это единичная матрица, то матрица
где Е это единичная матрица, то матрица
 называется обратной матрицей А.
Выражденой матрица называется квадратная
матрица определитель которой
называется обратной матрицей А.
Выражденой матрица называется квадратная
матрица определитель которой
 .
Для того чтобы данная матрица имела
обратную необходимо и достаточно чтобы
она была не выражденой.
.
Для того чтобы данная матрица имела
обратную необходимо и достаточно чтобы
она была не выражденой.

-
Решение системы линейных уравнений по формулам Крамера
Замечание: Формулы Крамера справедливы для систем с одинаковым количеством неизвестных и уравнений.


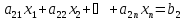

Определитель
n-ого
порядка
 элементами которого является коэффициент
при неизвестных
элементами которого является коэффициент
при неизвестных
 называется определителем системы. Если
определитель
называется определителем системы. Если
определитель
 ,
то система
,
то система
имеет единственное решение которое находится по формулам Крамера:
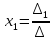

 ,
где
,
где
 -- определители n-ого
порядка полученные из определителя
-- определители n-ого
порядка полученные из определителя
 заменой 1-го, 2-го…n-ого
столбца соответственно столбцом
свободных членов.
заменой 1-го, 2-го…n-ого
столбца соответственно столбцом
свободных членов.
