Коэффициенты эластичности

Вид функции, у	Первая производная,	Коэффициент эластичности,
Линейная у = а + bx + ε	b
Парабола у = а + bx + cx2 + ε	b + 2cx
Гипербола у = а + + ε
Показательная у = а bxε	ln b a bx	Э = х lnb
Степенная у = а хb ε	a b xb-1	Э = b
Экспоненциальная у = еa+bxε	b еa+bx	Э = b х

2.3. Предпосылки мнк (условия Маркова-Гаусса)

Для получения по МНК наилучших результатов необходимо чтобы выполнялись следующие условия (предпосылки) относительно случайного отклонения ε.

1. Математическое ожидание случайного отклонения ε_i равно нулю: М(ε_i)=0, для всех наблюдений.

2. Дисперсия случайных отклонений ε_i постоянна D(ε_i)=D(ε_j)=σ² , для любых наблюдений i и j. Постоянство дисперсии называется гомоскедастичностью, непостоянство дисперсии называется гетероскедастичностью.

Н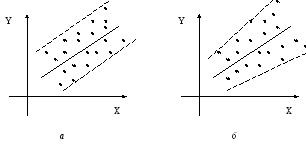 а рис.2.3.1, а показано постоянство дисперсии, на рис. 2.3.1, б показано непостоянство дисперсии

рис.2.3.1 Постоянство и непостоянство дисперсии отклонений

2. Случайные отклонения ε_i и ε_j являются независимыми друг от друга.

3. Случайное отклонение ε_j должно быть независимо от объясняющих переменных.

4. Ошибки ε_i подчиняются нормальному распределению.

F-тест Фишера на состоятельность регрессии

После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Оценка значимости уравнения регрессии в целом производится с помощью F – критерия Фишера. При этом выдвигается нулевая гипотеза H₀: уравнение регрессии статистически незначимо.

Для этого выполняется сравнение фактического (расчетного) критерия F_р с табличным значением F_табл. Таблицы критических значений составлены на основе двухпараметрического распределения неотрицательной случайной величины (F-распределения Фишера) в зависимости от численных значений степеней свободы v₁ = m и v₂ = n - m - 1, при различных уровнях значимости (в приложении 2 дана таблица F-распределения Фишера для трех различных значений уровня значимости 5%, 1%, 0,1%).

(3.7)

Если > F_табл при заданном уровне значимости α, гипотеза H₀ о случайной природе формирования уравнения регрессии отклоняется, то есть уравнение регрессии статистически значимо.

Если <F_табл при заданном уровне значимости α, гипотеза H₀ о случайной природе формирования уравнения регрессии не отклоняется и признается статистическая незначимость и ненадежность уравнения регрессии.

Анализ точности определения параметров регрессии

Для оценки статистической значимости параметров регрессии используют t – критерий Стьюдента. При этом выдвигается нулевая гипотеза H₀ : параметр b (a) статистически незначим (близок к нулю). При отклонении Н₀ параметр b (a) считается статистически значимым, что указывает на наличие определенной линейной зависимости между х и у.

Находится расчетное значение t – критерии для каждого параметра. Для параметра b:

(3.8)

для параметра a:

(3.9)

Полученные расчетные значения сравниваются с табличным (приложение 1) для заданного уровня значимости α и при ν=n-m-1 степенях свободы.

Если , то гипотеза H₀ о статистической незначимости параметра b отклоняется, то есть параметра b статистически значим.

Если , то гипотеза H₀ о статистической незначимости параметра а отклоняется, то есть параметра а статистически значим.

Если , то гипотеза H₀ о статистической незначимости параметра b принимается.

Если , то гипотеза H₀ о статистической незначимости параметра а принимается.

Стандартные ошибки параметров и самой линейной регрессии определяются по формулам:

Стандартная ошибка параметра b:

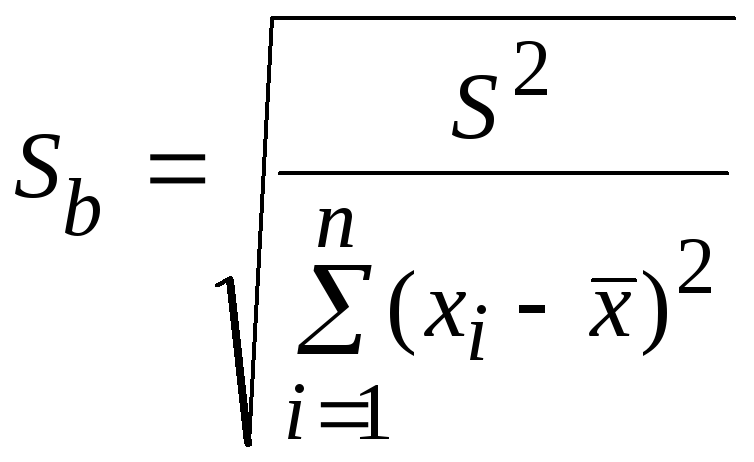(3.10)

Стандартная ошибка параметра а:

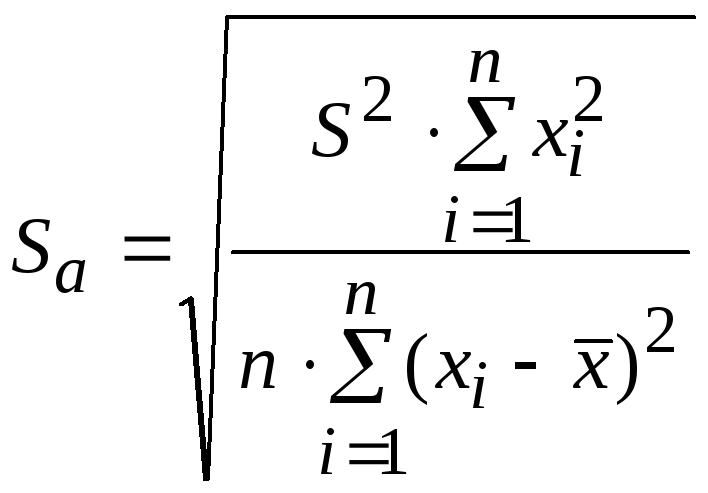(3.11)

Стандартная ошибка регрессии (мера разброса зависимой переменной вокруг линии регрессии):

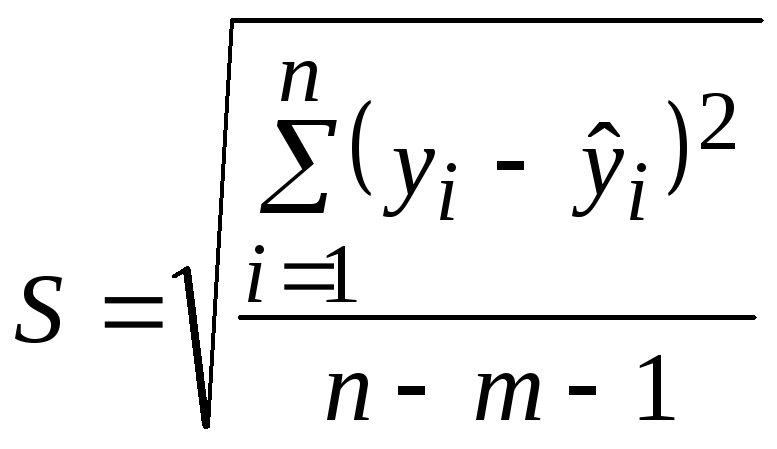(3.12)