Теорема котельникова и ее практическое значение

Для использования преимуществ цифровых устройств (недостатков) в системах передачи и обработки информации возникает необходимость в преобразовании непрерывных сигналов в дискретные. С этой целью наиболее часто используются методы дискретизации (квантование по времени) с постоянным шагом дискретизации. Методы равномерной дискретизации получили наиболее широкое распространение поскольку неравномерная дискретизация является крайне неудобной для тех целей, поскольку не позволяет осуществить качественную синхронизацию отдельных устройств СПД (систем передачи данных) и затруднителен процесс восстановления сигнала на приемной стороне.

В случае использования равномерной дискретизации возникает вопрос о выборе оптимального шага дискретизации.

В 1933 г. академиком В.А.Котельниковым была доказана теорема, играющая важную роль в теории информации (Шеннон претендовал на теорию информации)

ТЕОРЕМА:

Любая непрерывная функция y(t) частотный спектр которой ограничен сверху некоторым значением частоты может быть полностью и безошибочно восстановлена по ее дискретным значениям (отсчетам), взятым через интервал времени , при этом функция y(x) может быть представлена в виде следующего ряда:

t – текущее время

t_k – время когда берутся отсчеты

- функция отсчета.

Каждая функция отсчетов ψ_k представляет собой с точки зрения теории сигналов реакцию идеального фильтра низкой частоты, имеющего граничную частоту F_max.

ФНЧ

Из данной теоремы следует, что по заданным мгновенным значениям можно восстановить непрерывное сообщение y*t), пропуская импульсные значения его отсчетов через идеальный n-образный фильтр низкой частоты, имеющий полосу пропускания в диапазоне от 0 до F_max.

Процесс восстановления непрерывного сообщения по заданным выборкам (отсчетам) называется сглаживанием (интерполяцией).

В общем случае функции, используемые для разложения заданной функции могут представлять собой не только набор функций отсчетов ψ_k(t,t_k):

В качестве таких базисных функций могут использоваться: функции Уолела, Хаара. Конкретный выбор этих функций определяется условиями задачи, возникающей при прохождении сигналов через информационную систему (ИС).

Виды переносчиков сигналов и их характеристики. Способы формирования сигналов.

Для передачи и последующей обработке первичное сообщение необходимо нанести на подходящий материальный носитель. Чаще всего для этого используются процессы электромагнитной природы, имеющие непрерывный либо дискретный характер. Процесс нанесения информации на переносчик сводится к изменению характеристик используемого физического объекта в соответствии с первичным (принимаемым) сообщением. Параметры, используемые для нанесения информации называются информационными. Процесс управления информационными параметрами переносчика называется модуляцией. Обратная операция, заключающаяся в составлении исходного сообщения называется демодуляцией (детерминирование).

Техническая реализация этих операций осуществляется с помощью функциональных преобразователей сигналов называются модуляторами и демодуляторами.

Обычно эти устройства в рамках используемой информационной системы (ИС) образуют взаимосвязанную пару (модуль) работающих совместно с генератором сигналов переносчиков.

В зависимости от вида и числа используемых информационных параметров процесса-переносчика могут применяться различные виды модуляции.

В зависимости от числа используемых информационных параметров и характера их поведения во времени переносчики информации можно поделить на три типа:

1. Стационарные – это такие переносчики, которые характеризуются наличием (при отсутствии модуляции) постоянства во времени своего исходного состояния.

Такие переносчики фактически имеют только один информационный параметр. Модуляция такого рода переносчиков называется прямой модуляцией (ПМ).

2. Гармонические переносчики (процессы) (колебания, волны) к таким переносчикам относят процессы, происходящие в отсутствии модуляции по гармоническому закону:

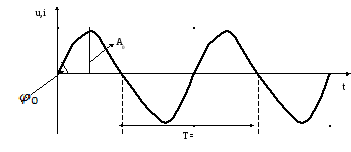
В качестве информационных параметров могут выступать соответственно различают амплитудную модуляцию, частотную модуляцию, фазовую модуляцию (АМ, ЧМ, ФМ).

3. Импульсные последовательности:

При использовании переносчиков третьего типа возникает возможность использования наиболее широкого ассортимента методов модуляции: АИМ, ЧИМ, ФИМ, ШИМ и комбинации модуляций.

Лекция №6

В зависимости от вида числа используемых информационных параметров, процесса переносчика могут применяться различные виды модуляции, а именно, если под действием первичного сигнала информационные параметры переносчика изменяются непрерывно, то такая модуляция называется непрерывной.

В качестве переносчика при осуществлении непрерывной модуляции чаще всего используют процессы в виде гармонических колебаний. В этом случае переносчик (несущая) обладают тремя информационными параметрами, что позволяет осуществлять три вида модуляции амплитудная модуляция (АМ), частотная модуляция (ЧМ) и фазовая модуляция (ФМ), а также их комбинации (многократные модуляции).