
лекции / Мет_Эйлер_5
.docМинистерство образования и науки Российской федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
Балаковский институт, техники, технологии и управления
МЕТОД ЭЙЛЕРА ДЛЯ АНАЛИЗА ДИНАМИЧЕСКОЙ МОДЕЛИ ТЕХНИЧЕСКОЙ СИСТЕМЫ
Методические указания к выполнению практической работы
по дисциплине «Моделирование систем» для студентов специальности 210100 всех форм обучения
Одобрено
редакционно-издательским советом
Балаковского института техники,
технологии и управления
Балаково 2009
ВВЕДЕНИЕ
Характеристики функционирования технической системы определяются ее внутренними физическими свойствами и внешними воздействиями: возмущающими и управляющими. Возмущающие воздействия оказывает внешняя среда, а управляющие - системы управления, предназначенные для обеспечения заданных характеристик. Для технической системы наиболее характерным является функционирование в условиях непрерывно изменяющихся внешних воздействий. Состояние системы при этом оказывается неустановившимся и характеризуется изменением во времени фазовых координат. Такой режим называется динамическим и описывается дифференциальными уравнениями. Данные методические указания являются пятой работой по разработке и анализу математических моделей
Цель работы: выполнить анализ гидравлической системы с использованием неявного метода Эйлера.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
В общем, случаи математическая модель представляет собой систему обыкновенных дифференциальных уравнений вида:
|
|
(1) |
где ![]() - вектор фазовых координат системы;
- вектор фазовых координат системы;
![]() - вектор производных
фазовых координат по t;
- вектор производных
фазовых координат по t;
![]() - вектор внешних
воздействий.
- вектор внешних
воздействий.
В зависимости от
характера изменения воздействия
![]() и описания внутренних физических свойств
системы, ее модель может быть
детерминированной или вероятной.
Функциональное проектирование технической
системы на основе модельных режимов, в
число которых входит переходный процесс
– переходный процесс системы называется
переход системы из одного установившегося
состояния в другое. Моделирование
переходного процесса позволяет
исследовать быстродействие, точность,
динамичность, колебательность и другие
свойства системы.
и описания внутренних физических свойств
системы, ее модель может быть
детерминированной или вероятной.
Функциональное проектирование технической
системы на основе модельных режимов, в
число которых входит переходный процесс
– переходный процесс системы называется
переход системы из одного установившегося
состояния в другое. Моделирование
переходного процесса позволяет
исследовать быстродействие, точность,
динамичность, колебательность и другие
свойства системы.
Решение задач анализа переходного процесса, включает три этапа:
1) Интегрирование системы дифференциального уравнения (1).
2) Определение показателей качества.
3) Оценка степени выполнения технических требований к системе.
В данной работе используется метод Эйлера для интегрирования системы дифференциальных уравнений. Для его реализации выполняются следующие этапы.
1) Формирование матрицы Якоби в динамической модели.
Матрица Якоби динамической модели составляется аналогично статической. В общем случае, система дифференциальных уравнений:
|
|
(2) |
где, ![]()
![]()
![]()
A - матрица Якоби;
![]() - вектор фазовых
координат
- вектор фазовых
координат
![]() ;
;
![]() - вектор функции
внешних воздействий
- вектор функции
внешних воздействий
![]() .
.
2) Выбор параметров интегрирования.
Пусть переходный процесс оценивается, как реакция системы находящейся в состоянии покоя на ступенчатом воздействии вида:
|
|
(3) |
где V0 и Vk – начальное и конечное значение функции воздействия U(t),
причем: V0=const, Vk=const.
Начальные и конечные значения определяются при анализе статической модели системы.
Если система устойчива, то через некоторый период времени, система перейдет из одного состояния V0 в Vk , в противном случае конечных значений не достигнет.
Записывается
вектор входных воздействий U
при
![]() .
При чем, используются значения, при
которых определялся вектор фазовых
координат Vk.
.
При чем, используются значения, при
которых определялся вектор фазовых
координат Vk.
Выбор шага интегрирования h неявного метода Эйлера осуществляется исходя из условия устойчивости метода (устойчивости системы):
|
|
(4) |
где h – шаг интегрирования;
λ - собственные значения матрицы Якоби.
Для комплексных значений λ, условие устойчивости имеет вид:
|
|
(5) |
Собственными
значениями матрицы Якоби порядка n
– называют корни λk,
где k
=![]() ее характеристического уравнения:
ее характеристического уравнения:
|
|
(6) |
где Е – единичная матрица.
3) Решение системы дифференциального уравнения методом Эйлера
Формула численного интегрирования неявного метода Эйлера имеет вид:
|
|
(7) |
где ![]() - определяется из исходной системы
дифференциальных уравнений
- определяется из исходной системы
дифференциальных уравнений
![]()
Совместное преобразование последних двух выражений приводит к следующей зависимости:
|
|
(8) |
где
![]() -
модифицированная матрица Якоби, на к+1
шаге пересчитывается, исходя из элементов
к-ого шага по формуле:
-
модифицированная матрица Якоби, на к+1
шаге пересчитывается, исходя из элементов
к-ого шага по формуле:
|
|
(9) |
Остальные элементы не изменяются, например:
|
|
(10) |
![]() модифицированный
вектор входных воздействий, на к+1 шаге,
определяемый по формуле:
модифицированный
вектор входных воздействий, на к+1 шаге,
определяемый по формуле:
|
|
(11) |
Например,
|
|
(12) |
Решение системы
уравнений
![]() ,
дает значение фазовых координат на к+1
шаге, то есть в момент времени tk+1.
,
дает значение фазовых координат на к+1
шаге, то есть в момент времени tk+1.
Алгоритм неявного метода Эйлера с постоянным шагом h:
-
Задание шага интегрирование h.
-
Задание начальных значений
 при
при
 .
. -
Вычисление времени
 .
. -
Вычисление матрицы
 и
и
 на к+1шаге.
на к+1шаге. -
Решение системы уравнений
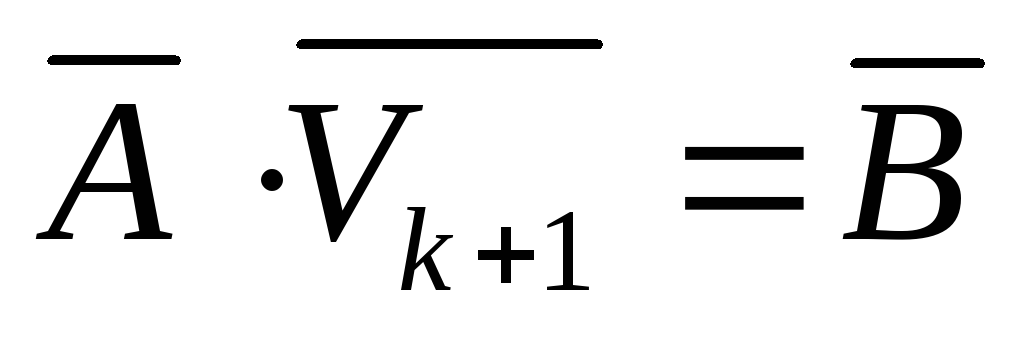 ,
с целью определения
,
с целью определения
 на временном участке tk+1.
на временном участке tk+1.
Использование данного метода позволяет построить графики переходных процессов, на основании которых определяются показатели качества и оценивается выполнение требований при проектировании технической системы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
-
Ознакомится с теоретическим материалом.
-
На основании динамической модели гидравлической системы, полученной с использованием узлового метода (третья работа) записать матрицу Якоби.
-
Записать вектор начальных и конечных состояний фазовых координат, вектор внешних воздействий.
-
Осуществить выбор шага интегрирования.
-
Реализовать алгоритм неявного метода Эйлера.
-
Построить переходные процессы. Определить показатели качества.
-
Составить отчет по работе
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
Пусть дана система дифференциальных уравнений, характеризующая динамическую модель гидравлической системы, полученной с использованием узлового метода:
|
|
(13) |
Так как система дифференциальных уравнений нелинейная, то элементами матрицы Якоби, являются частные производные по фазовым координатам:
|
|
(14) |
Матрица Якоби в
динамическом случае переменная, ее
элементы зависят от фазовых координат
системы - расходов жидкости
![]() .
.
Пусть начальное и конечное значения заданы в виде (рассчитаны с использованием статической модели в четвертой работе):


Вектор входных
воздействий при
![]() :
:

Произведем расчет значений матрицы Якоби с учетом начальных значений расходов:

Запишем единичную матрицу:

Тогда характеристическое уравнение имеет вид:
![]()
Вычислив корни характеристического уравнения, найдены собственные значения матрицы Якоби:

Все корни характеристического уравнения имеют отрицательные действительные части, что говорит об устойчивости самой системы. Отсутствие комплексно – сопряженных дает монотонный процесс ряда фазовых координат. Рекомендуемый шаг интегрирования равный h=0.5. Выполним проверку устойчивости, методом Эйлера при данном шаге:
![]()
![]()
![]()
![]()
Следовательно, шаг h=0.5 обеспечит, устойчивость метода, то есть приемлемую точность вычислений.
Программа в Маткад, реализующая данный алгоритм имеет вид


![]()

Построим переходные процессы.

Рисунок 1 – Переходные процессы системы (расходы)

Рисунок 2 – Переходный процесс системы (давление)
ВАРИАНТЫ ЗАДАНИЙ
Метод Эйлера реализуется на основании системы дифференциальных уравнений, описывающих гидравлическую систему, полученную в результате выполнения третьей работы с использованием узлового метода.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
-
Понятие детерминированной модели.
-
Задачи анализа переходных процессов.
-
Алгоритм неявного метода Эйлера.
-
Собственные значения матрицы Якоби.
-
Устойчивость метода интегрирования.
-
Элементы программирования в Маткад.
ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ РАБОТЫ
1. Подготовка к работе – 1,0 акад.час
2. Выполнение работы – 2,0 акад.часа
3. Оформление работы – 1,0 акад.час
ПОРЯДОК ОФОРМЛЕНИЯ ОТЧЕТА
1. Название практической работы.
2. Цель работы. Задание.
3. Краткие теоретические сведения.
4. Расчетная часть.
ЛИТЕРАТУРА
1. Тарасик В.П. Математическое моделирование технических систем: учебник для вузов / В.П.Тарасик. – Мн.: ДизайнПРО, 2004. – 640с.: ил.
СОДЕРЖАНИЕ
1. Введение 2
2. Основные теоретические сведения 2
3. Порядок выполнения работы 6
4. Пример выполнения работы 6
5. Варианты задания 10
6. Вопросы для самопроверки 10
7. Время, отведенное на выполнение работы 10
8. Порядок оформления отчета 11
Литература 11
МЕТОД ЭЙЛЕРА ДЛЯ АНАЛИЗА ДИНАМИЧЕСКОЙ МОДЕЛИ ТЕХНИЧЕСКОЙ СИСТЕМЫ
Методические указания к выполнению практической работы
по дисциплине «Моделирование систем» для студентов специальности 210100 всех форм обучения
Составил: Мефедова Юлия Александровна
Рецензент Т.Н. Скоробогатова
Редактор Л.В.Максимова
Корректор А.М.Рогачева
|
Подписано в печать |
|
Формат 60х84 1/16 |
|
Бумага тип. |
Усл. печ. л. 0,75 |
Уч.-изд.л. 0,659 |
|
Тираж 100 экз. |
Заказ |
Бесплатно |
Саратовский государственный технический университет
410054, г.Саратов, ул.Политехническая, 77
К опипринтер
БИТТиУ, 413840, г.Балаково, ул. Чапаева, 140
опипринтер
БИТТиУ, 413840, г.Балаково, ул. Чапаева, 140




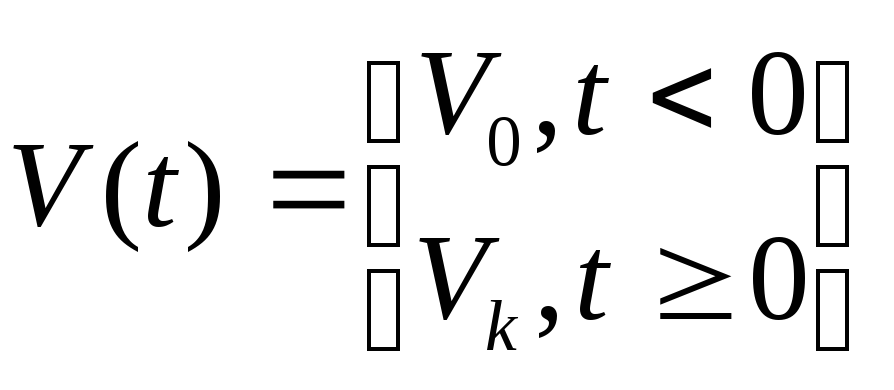
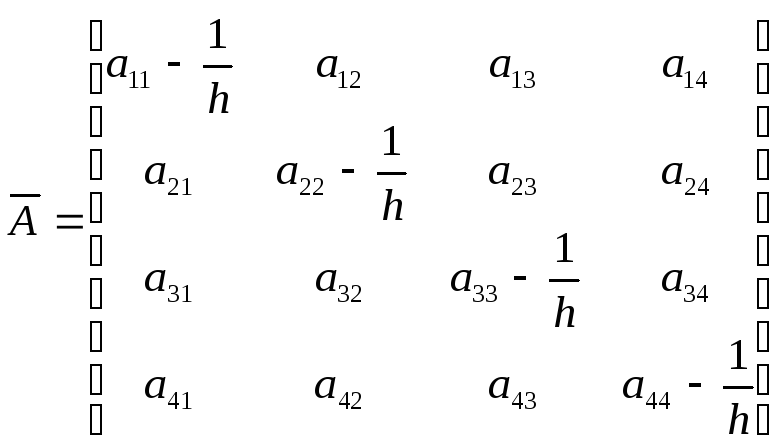

 .
. .
.