1 0 0 0 1 0 1 →F8(X).

Последовательность элементов <к2к1к0>→101 является строкой матрицы дополнений. Переименовав элементы Kj переменными Pj (j=0,l,2 для данного кода) и заменив нули переменными j, а единицы - Pj (без инверсии), получим

<101>→ p21p0=z5

Единица, стоящая в этой же строке единичной транспонированной матрицы, указывает, что найденное выражение z5 является опознавателем ошибки в элементе <а3>. Аналогично находятся другие опознаватели.

Сравнивая между собой (поэлементно) выражения (9), замечаем, что некоторые из них отличаются только значением одной переменной. Следовательно, возникновение 2-х ошибок может привести к трансформации передаваемого сообщения (d=3; r=s=1).

Процедура исправления ошибок описывается логическими выражениями:

α0=ā0z3; α1=ā1z6; α2=ā2а4; α3=ā3z5. (10)

Целесообразно для реализации зависимостей (10) использовать отдельный ДШ опознавателей, если число проверок k (и контрольных элементов) циклического кода не превышает 5.6. В противном случае (при k>6) наименьшие аппаратные затраты будут, если в качестве ДШ опознавателей применить соответствующим образом запрограммированное ППЗУ в интегральном исполнении.

Методы подготовки данных для программирования ППЗУ на реализацию логических функций с известными алгебраическими выражениями изложены в [3,с.91-93], [4, с. 144-162].

А на рис.7 приведена функциональная схема декодирования циклического (7,4) – кода с исправлением одиночных ошибок в его информационных элементах. Сравнивая рис. 5-7, нетрудно заметить идентичность и простоту их структур. Конечно, сложность ДШ циклических кодов, исправляющих большее число ошибок (s>1), существенно возрастает из-за усложнения ДШ опознавателей.

Рассмотрим процедуры отыскания данных для построения комбинационного ДШ «усеченного» циклического (15,7)-кода, исправляющего одиночные и двойные ошибки в информационных элементах (d=5,s=r=2). Возьмем псевдоциклический (12,4)-код [1,с.63] с образующей матрицей

a3 a2 a1 a0 k7 k6 k5 k4 k3 k2 k1 k0

(11)

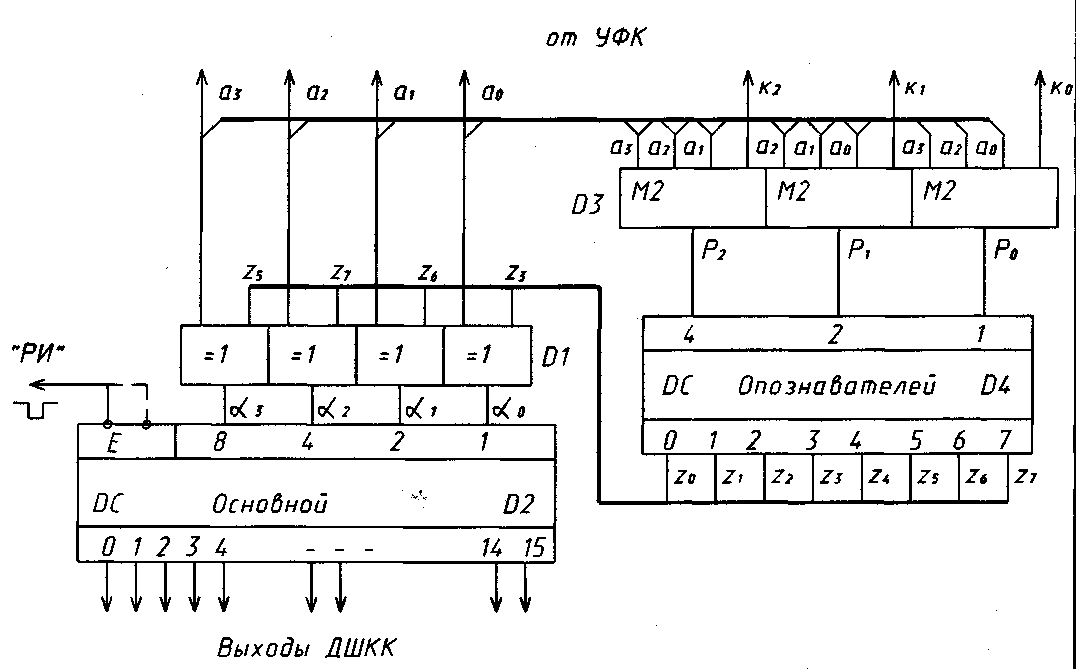
Рис. 7. Комбинационный ДШ циклического (7,4) – кода

Запишем алгебраические выражения проверок на четность, пользуясь (11) и выше изложенной методикой:

(12)

Опознаватели будем записывать с индексами информационных элементов, в которых должны исправляться ошибки. Тогда опознаватели одиночных ошибок будут иметь вид:

z0=p7p65p4321p0→1101.0001=D1H, z1=7p6p5p432p1p0 → 0111.0011=73H, (13)

z2=p7p6p543p2p10 → 1110.0110=C6Н,

z3=765p4p3p21p0 → 0001.1101=1DH.

Известно, что опознаватели двойных ошибок находятся как поразрядная сумма по mod 2 опознавателей соответствующих одиночных ошибок. Так как число информационных элементов у данного кода 4, то опознавателей двукратных ошибок будет 6 (С ):

z01=p76p5432p10 → 1010.0010=A2H,

z02=76p5p43p2p1p0 → 0111.0011=73H,

z03=p7p654p3p210 → 1100.1100=CCH,

z12=p765p43p21p0 → 1001.0101=95H, (14)

z13=7p6p54p3p2p10 → 0110.1110=6EH,

z23=p7p6p5p4p32p1p0 → 1111.1011=FBH.

Если запрограммировать ППЗУ на реализацию выражений (13) и (14), то такой ДШ опознавателей сможет выдать сигналы коррекции всех одиночных и двойных ошибок при условии, что они находятся только на информационных позициях. По выражениям (12) нетрудно убедиться, что одиночная ошибка в контрольных элементах отображается опознавателем вида 76543210, у которого только одна переменная р не имеет знака инверсии. Следовательно, двум ошибкам, одна из которых находится на контрольной, а другая на информационной позициях, будет соответствовать опознаватель, отличающийся от выражений (13) только одним элементом (всего таких опознавателей 4∙8=32). Итак, чтобы исправить одиночную ошибку на информационных позициях <а3>, ..., <а0> при наличии второй на контрольных, необходимо к выражениям (13) добавить дизъюнктивно (по ИЛИ) 8 опознавателей двойных ошибок. А чтобы исправить две ошибки на информационных позициях, дополнительно к получаемым выражениям, надо дизъюнктивно «прибавить» соответствующие опознаватели (14).

Воспользуемся цифровой формой задания логических функций [1] 16-ричной системой записи двоичных чисел, отображающих опознаватели. Так правые части выражений (13), (14) иллюстрируют последовательный переход от алгебраической формы к цифровой - сначала в двоичный, а затем в n-мерной системе счисления.

С учетом сказанного, логические функции, описывающие выходные сигналы ППЗУ, используемые для коррекции ошибок (одиночных и двойных) на информационных позициях рассматриваемого кода, могут быть представлены следующими выражениями:

Za0(1)={R1,D0,D3,D5,D9,51,91,C1,F1,A2,37,CC}, Za1(1)={73,72,71,77,78,63,33,53,F3,A2,95,6E}, Za2(1)=(E6,E4,E7,E2,EE,66,A6,C6,F6,37,95,FB}, (15)

Za3( 1 )= {1D, 19,15,1F, 1 C,1D,3D,5D,9D,CC,6E,FB}.

Они будут корректными, если при переходе к алгебраической форме строго придерживаться последовательности записи аргументов:

<p7p6p5p4p3p2p1p0> (16)

В (16) р0 является переменной самого младшего разряда, а переменная р7 -самого старшего (с «весом» W=2 =<128>) разряда. Выражения (15) и последовательность (16) содержат полную информацию для выбора и программирования ППЗУ: (16) указывает необходимое число и порядок подачи сигналов на адресные входы; а (15) содержит список адресов, по которым должны быть записаны единицы при программировании отдельных выходов ППЗУ, обозначенных функциями Za0, Za1, Za2 и Za3. Таким образом, для реализации декодера опознавателей потребуется ППЗУ с 8 адресными входами и 4 выходами (емкость памяти 2∙4=1Кбит).

На рис.8 представлена функциональная схема узла формирования сигналов коррекции для комбинационного ДШ, рассмотренного псевдоциклического (12,4)-кода. Узел состоит из схемы реализации проверок (12) (это сумматоры D1,...,D10) и ДШ опознавателей на ППЗУ D11, запрограммированного на реализацию выражений (15).

Полную схему ДШКК этого кода легко получить на рис.7, если заменить «элементы» D3 и D4 схемой (рис.8.) Такой ДШКК позволит исправить любую одиночную и двойную ошибки, на каких бы позициях кодовой комбинации они не возникли. Вместе с тем, три ошибки приведут к трансформации переданного сообщения.

Достоинствами приведенных ДШ являются их высокое быстродействие, простота в настройке и управлении. К недостаткам следует отнести необходимость предварительной фиксации всех элементов (информационных, контрольных) принимаемой комбинации. Помимо комбинационных ДШ существуют декодирующие устройства циклических кодов последовательного типа. С ними можно ознакомиться по учебным пособиям [4,5].

Литература

1. Громаков Е.И., Собакин Е.Л. Логические устройства и их применение в автоматике: Учебное пособие. Томск, изд.ТПИ, 1982 - 95с.

2. Собакин Е.Л. Проектирование устройств телеуправления телесигнализации. : Учебное пособие по курсовому проектированию.- Томск, изд.ТПИ, 1983-95с.

3. Пупырев Е.И. Перестраиваемые автоматы и микропроцессорные системы.-М.: Наука, 1984-192с.

4. Тутевич В.Н. Телемеханика: Учебное пособие для вузов.-М.: Энергия, 1973-384с.; то же-2-е изд., перераб. и доп.-М.:Высшая школа, 1985-423с.

5. Ильин В.А. Телеуправление и телеизмерение.: Учебное пособие для вузов.-3-е изд., перераб. и доп.-М.:Энергоиздат., 1982-560 с.