
лекции / Мет_Ньютона_4
.docМинистерство образования и науки Российской федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
Балаковский институт, техники, технологии и управления
МЕТОД НЬЮТОНА ДЛЯ АНАЛИЗА СТАТИЧЕСКОЙ МОДЕЛИ ТЕХНИЧЕСКОЙ СИСТЕМЫ
Методические указания к выполнению практической работы
по дисциплине «Моделирование систем» для студентов специальности 210100 всех форм обучения
Одобрено
редакционно-издательским советом
Балаковского института техники,
технологии и управления
Балаково 2009
ВВЕДЕНИЕ
Режим функционирования технической системы определяется характером внешних возмущающих и управляющих воздействий. Различают статический и динамический режимы. При постоянных воздействиях система находится в уставившемся равновесном состоянии (статический режим) и ее фазовые переменные при этом постоянные. При этом статический режим характеризуется двумя состояниями: равномерное установившееся движение; состояние покоя. Данные методические указания являются четвертой работой по разработке и анализу математических моделей
Цель работы: выполнить анализ гидравлической системы в статическом режиме с использованием численного метода Ньютона.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определяющий признак статического режима для технической системы любой физической природы – постоянство во времени всех фазовых переменных типа потока и типа потенциала, характеризующих состояние всех ее элементов.
Существует несколько подходов к постановке и решению задач анализа статических состояний технических систем. В общем виде математическая модель в статическом состоянии представляет собой систему линейных или нелинейных алгебраических уравнений вида:
|
|
(1) |
где ![]() -
вектор фазовых координат технической
системы.
-
вектор фазовых координат технической
системы.
Данная модель может быть получена из исходной математической модели технической системы, представляющей собой на макроуровне систему дифференциальных уравнений вида:
|
|
(2) |
Численное решение
уравнения (2) при неизменных внешних
воздействиях через конечный отрезок
времени tk
приводит к стационарной точке V*,
в которой
![]() .
Координаты этой точки будут соответствовать
искомому решению.
.
Координаты этой точки будут соответствовать
искомому решению.
Различают прямые и итерационные (численные) методы решения систем алгебраических уравнений. В данных методических указаниях рассмотрим численный метод Ньютона, так как он обладает наибольшей скоростью сходимости среди практически применяемых методов.
В общем случае алгоритм любого итерационного метода может быть представлен выражением вида:
|
|
(3) |
где ![]() -
вектор функции, определяемый способом
построения итерационного процесса;
-
вектор функции, определяемый способом
построения итерационного процесса;
![]() -
вектор искомых фазовых переменных
предыдущих вычислений;
-
вектор искомых фазовых переменных
предыдущих вычислений;
![]() -
вектор искомых фазовых переменных
последующих вычислений.
-
вектор искомых фазовых переменных
последующих вычислений.
Переход от очередного
вектора
![]() к
к
![]() -
итерация.
-
итерация.
Итерационная формула Ньютона имеет вид:
|
|
(4) |
где ![]() -
значение матрицы Якоби состояния фазовых
координат системы.
-
значение матрицы Якоби состояния фазовых
координат системы.
Алгоритм метода Ньютона включает следующие этапы:
-
Выбор начального приближения
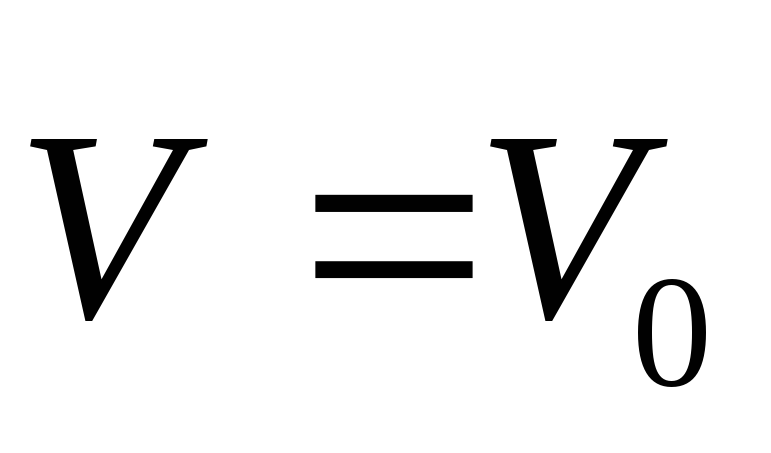 ;
; -
Вычисление матрицы Якоби Jk в точке
 (k=0,
1, 2 …);
(k=0,
1, 2 …);
-
Вычисление вектора невязок
 исходной системы алгебраических
уравнений;
исходной системы алгебраических
уравнений; -
Решение итерационной формулы методом Ньютона и определения нового приближения вектора искомых фазовых переменных
 ;
; -
Вычисление нормы вектора невязок
 и нормы вектора поправок
и нормы вектора поправок
 ;
; -
Проверка условия окончания итерационного процесса:
 ,
,
 ;
где
;
где
 -
малые положительные числа, косвенно
характеризующие точность полученного
решения.
-
малые положительные числа, косвенно
характеризующие точность полученного
решения.
Норма вектора невязок системы алгебраических уравнений определяется исходя из следующего выражения:
|
|
(5) |
где n – порядок системы алгебраических уравнений,
![]() -
невязка i-того
уравнения системы на которой итерации.
-
невязка i-того
уравнения системы на которой итерации.
Норма вектора поправок на k+1-ой итерации – вектор, рассчитываемый по формуле:
|
|
(6) |
.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
-
Ознакомится с теоретическим материалом.
-
На основании динамической модели гидравлической системы, полученной с использованием узлового метода (третья работа) записать модель в статическом режиме.
-
Записать матрицу Якоби статической модели.
-
Реализовать алгоритм метода Ньютона.
-
Рассчитать значения фазовых координат для двух значений расходов (давлений) насоса.
-
Составить отчет по работе
ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ
Пусть дана система дифференциальных уравнений, характеризующая динамическую модель гидравлической системы, полученной с использованием узлового метода:
|
|
(7) |
При постоянных внешних воздействиях система находится в установившемся равновесном состоянии. Её фазовые координаты при этом постоянны, такой режим функционирования системы называется статический. Статическое состояние гидросистемы достигается при постоянных внешних воздействиях:
1) подачей насосов Qн1,Qн2;
2) давлениями потребителей Рв1,Рв2, Рв3.
При этом устанавливаются постоянные значения фазовых координат:
1) расходы в гидромагистралях Q1, Q2, Q3, Q4;
2) давление в упругих элементах Ру1, Ру2.
Полагая
![]() и
и
![]() ,
получим следующую систему нелинейных
алгебраических элементов:
,
получим следующую систему нелинейных
алгебраических элементов:
|
|
(8) |
Компонентное уравнение в диссипативных элементах в гидросистеме носит более сложный характер. При этом выделяют линейные и нелинейные потери давления в гидромагистрали и их компонентные уравнения, запишутся виде:
|
|
(9) |
где
![]() – коэффициент гидравлического
сопротивления, характеризующий линейные
потери при ламинарном режиме движения
жидкости.
– коэффициент гидравлического
сопротивления, характеризующий линейные
потери при ламинарном режиме движения
жидкости.
![]() – коэффициент
гидросопротивления характеризующий
нелинейные потери при турбулентном
режиме движения жидкости.
– коэффициент
гидросопротивления характеризующий
нелинейные потери при турбулентном
режиме движения жидкости.
С учетом уравнения (9), преобразуем систему к следующему виду:
|
|
(10) |
Полученная система уравнений является статической моделью системы, где в правой части известны значения входных воздействий. Для ее решения используется различные численные методы, для которых предварительно необходимо составить матрицу Якоби.
Матрица Якоби характеризует важнейшие свойства физической системы, а так же свойства уравнений математической модели. Элементами матрицы Якоби, являются частные производные от нелинейной вектор функции F(V) = (f1,f2 …fn) по фазовым коэффициентам системы (Q1, Q2, Q3, Q4, Ру1, Ру2), т.е.:
|
|
(11) |
В системе уравнений,
нелинейной является функция
![]() ,
для них частные производные имеют вид:
,
для них частные производные имеют вид:
|
|
(12) |
Тогда матрица Якоби, исследуемой гидросистемы, имеет вид:
 Для
решения статической модели используем
численный метод Ньютона, алгоритм
которого включает следующие этапы:
Для
решения статической модели используем
численный метод Ньютона, алгоритм
которого включает следующие этапы:
– выбор начального
приближения
![]() ,
,
где ![]() – вектор фазовых координат (Q1,
Q2,
Q3,
Q4,
Ру1,
Ру2),
– вектор фазовых координат (Q1,
Q2,
Q3,
Q4,
Ру1,
Ру2),
![]() – нулевой
вектор-столбец;
– нулевой
вектор-столбец;
– вычисление
матрицы Якоби
![]() в точке
в точке
![]() (k=0,
1 2 …);
(k=0,
1 2 …);
– вычисление
вектора невязок
![]() .
Вектор невязок получается из системы
уравнений (10) для статического режима:
.
Вектор невязок получается из системы
уравнений (10) для статического режима:

– определение вектора поправок:
![]() .
.
– определение нового приближения вектора искомых фазовых переменных:
![]() .
.
– проверка условий
окончания итерационного процесса, при
выполнении условия, что
![]() и
и
![]() соизмеримы (совпадают до десятых), иначе
осуществляется переход на предыдущие
этапы и вычисляется следующая итерация.
соизмеримы (совпадают до десятых), иначе
осуществляется переход на предыдущие
этапы и вычисляется следующая итерация.
Расчет фазовых координат при статическом процессе произведен в математическом пакете MathCad (рис.1). Результаты вычислений представлены в таблице 1
Таблица 1 – Результаты статического анализа
|
Фазовые координаты |
Qн1=200*10-6 м3/c Qн2=0*10-6 м3/c |
Qн1=200*10-6 м3/c Qн2=400*10-6 м3/c |
|
Q1, м3/c |
|
|
|
Q2, м3/c |
|
|
|
Q3, м3/c |
|
|
|
Q4, м3/c |
|
|
|
Ру1, Па |
|
|
|
Ру2, Па |
|
|

Рис.1 – Программа для расчета статической модели в MathCAD
ВАРИАНТЫ ЗАДАНИЙ
Метод Ньютона реализуется на основании системы дифференциальных уравнений, описывающих гидравлическую систему, полученную в результате выполнения третьей работы с использованием узлового метода.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
-
Понятие статического режима функционирования технической системы. Способ получение статической модели.
-
Принцип формирования матрицы Якоби.
-
Алгоритм численного метода Ньютона.
ВРЕМЯ, ОТВЕДЕННОЕ НА ВЫПОЛНЕНИЕ РАБОТЫ
1. Подготовка к работе – 1,0 акад.час
2. Выполнение работы – 2,0 акад.часа
3. Оформление работы – 1,0 акад.час
ПОРЯДОК ОФОРМЛЕНИЯ ОТЧЕТА
1. Название практической работы.
2. Цель работы. Задание.
3. Краткие теоретические сведения.
4. Расчетная часть.
ЛИТЕРАТУРА
1. Тарасик В.П. Математическое моделирование технических систем: учебник для вузов / В.П.Тарасик. – Мн.: ДизайнПРО, 2004. – 640с.: ил.
СОДЕРЖАНИЕ
1. Введение 2
2. Основные теоретические сведения 2
3. Порядок выполнения работы 6
4. Пример выполнения работы 6
5. Варианты задания 10
6. Вопросы для самопроверки 10
7. Время, отведенное на выполнение работы 10
8. Порядок оформления отчета 11
Литература 11
МЕТОД НЬЮТОНА ДЛЯ АНАЛИЗА СТАТИЧЕСКОЙ МОДЕЛИ ТЕХНИЧЕСКОЙ СИСТЕМЫ
Методические указания к выполнению практической работы
по дисциплине «Моделирование систем» для студентов специальности 210100 всех форм обучения
Составил: Мефедова Юлия Александровна
Рецензент Т.Н. Скоробогатова
Редактор Л.В.Максимова
Корректор А.М.Рогачева
|
Подписано в печать |
|
Формат 60х84 1/16 |
|
Бумага тип. |
Усл. печ. л. 0,75 |
Уч.-изд.л. 0,659 |
|
Тираж 100 экз. |
Заказ |
Бесплатно |
Саратовский государственный технический университет
410054, г.Саратов, ул.Политехническая, 77
К опипринтер
БИТТиУ, 413840, г.Балаково, ул. Чапаева, 140
опипринтер
БИТТиУ, 413840, г.Балаково, ул. Чапаева, 140




 .
.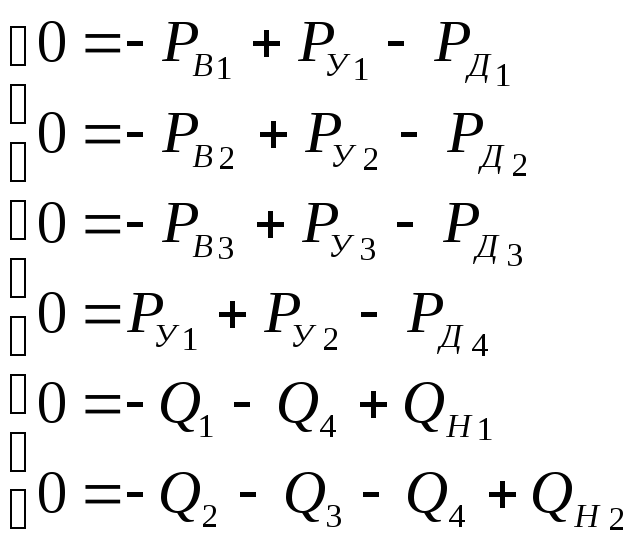 .
. .
. .
. .
.