1. Исследование зависимости величины относительной суммарной длины линий связи от взаимного расположения объектов I и II ступеней

Согласно варианту, в задании к курсовой работе была предложена для исследования трехступенчатая иерархическая структура информационно-измерительной системы, конфигурация которой представлена на рисунке 1.

Совместим объекты первой ступени с осью Х прямоугольной системы координат (рисунок 2).

y

III ступень

II ступень

L₂

L₃

I ступень

x

Рисунок 2 – Конфигурация ИИС в декартовой системе координат

Положение каждого объекта в прямоугольной системе координат задается двумя параметрами. Обозначим их для объектов первой ступени x_1i, y_1i, второй ступени x_2j, y_2j и для объектов третей ступени x₃, y₃.

Суммарная длина линий связи между объектами первой и второй ступеней определяется , (1)

а между объектами второй и третей ступеней

(2)

Общая длина линий связи ИИС

(3)

Расстояние до второй и третей ступени обозначено соответственно l₂ и l₃, значения величин l₂ и l₃ являются исходными данными к работе:

l₂ = 5,

l₃ = 20.

Обозначим l₂/l₃=a. То есть а =5/20 = 0,25.

Учитывая, что y_2j=l₂, y₃=l₃, получим

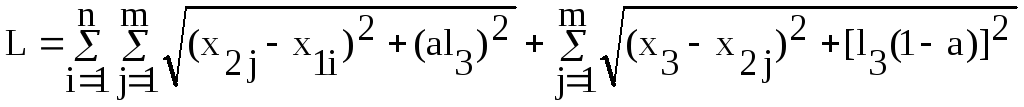(4)

Подставим в (4) значения Х₁₁ = 10, Х₁₂ = 20, Х₁₃ = 30, Х₁₄ = 35, Х₁₅ = 40, Х₂₁ = 10, Х₂₂ = 15, Х₂₃ = 30, Х₂₄ = 45, Х₂₅ = 40, Х₃₁ = 45 и а = 0,25.

При а=1 длина L достигает максимального значения

Зависимость L/L_M=f(a) при значениях а, принадлежащих отрезку [0; 1] представлена в таблице 1 и на рисунке 3.

Таблица 1

а	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
	3,542	3,56	3,631	3,743	3,889	4,061	4,255	4,469	4,7	4,948	5,214

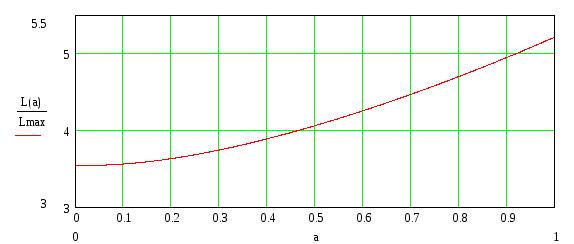
Рисунок 3 – Зависимость величины относительной суммарной длины линий связи от взаимного расположения объектов I и II ступеней

В задании указано взаимное расположение объектов I и II ступеней посредством значений величин l₂ и l₃, то есть, как уже вычислялось ранее, а =5/20 = 0,25. При таком значении а относительная суммарная длина линий связи составляет 3,682. Судя по графику, эта величина не является минимальной. Следовательно, можно оптимизировать размещение объектов таким образом, чтобы суммарная длина линий связи оказалась меньше, чем при данных условиях. Учитывая приведённый выше расчёт, следует предложить изменение отношения величин l₂ и l₃, сделав коэффициент а равным 0,1.

2. Исследование зависимости величины относительной суммарной длины линий связи от числа ступеней

Известно, что общая длина линий связи зависит от числа ступеней р и коэффициента ветвления в иерархической структуре. Количество ступеней р и коэффициент ветвления связаны между собой соотношением

, (5)

где n₁ – количество объектов первой ступени.

В предлагаемой для рассмотрения системе количество ступеней р = 3, количество объектов первой ступени n₁ = 5. Тогда, подставив известные величины в формулу (5), можно рассчитать коэффициент ветвления:

Общая длина линий связи находится суммированием длины линий связи по всем ступеням:

(6)

где l_i – суммарная длина линий связи i-ступени.

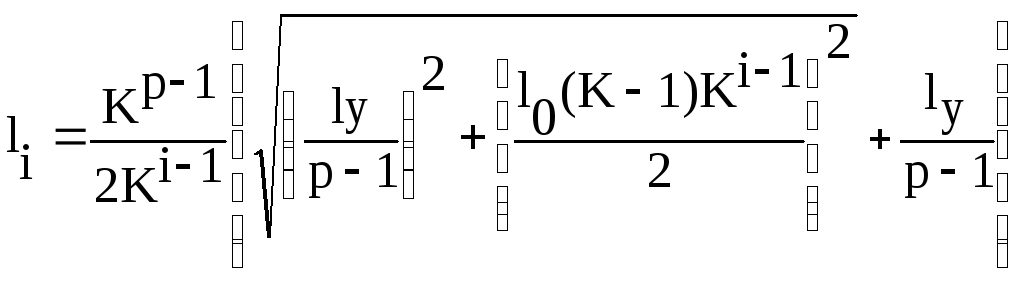, (7)

где l₀ – среднее расстояние между объектами, l₀ = 5;

l_y – расстояние от центрального органа управления до объектов I ступени, l_y = 20.

Рассчитаем суммарную длину линий связи для каждой ступени.

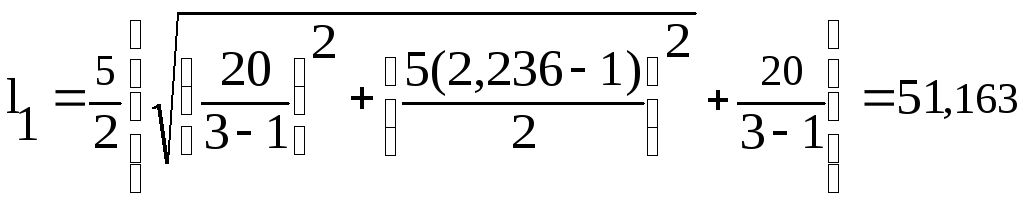
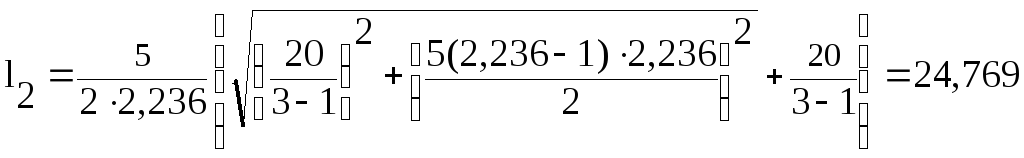
Тогда общая длина линий связи составит:

L = 51,163 + 24,769 + 14,202 = 90,134.

При р = 2 общая длина линий связи максимальна и её можно рассчитать по следующей формуле:

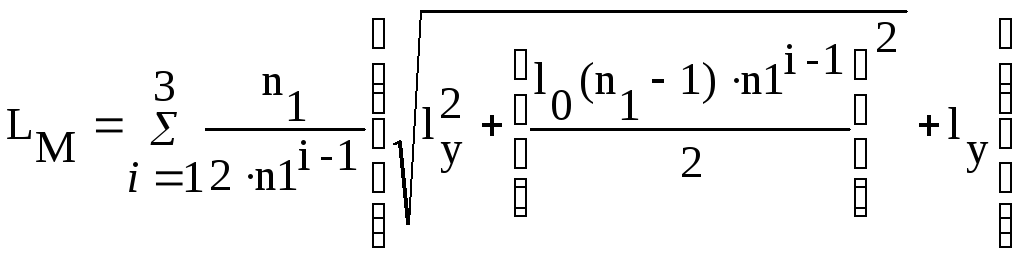. (8)

То есть относительная суммарная длина линий связи при количестве ступеней, равным 3, составит .

Построим зависимость величины относительной суммарной длины линий связи от числа ступеней (рисунок 4)

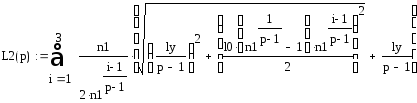(9)

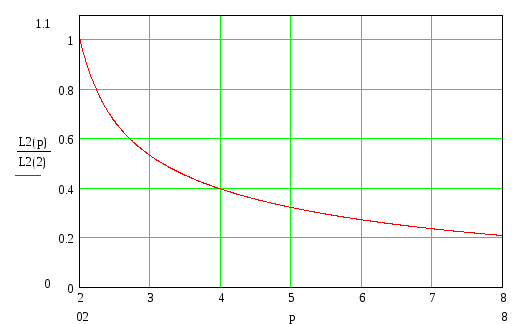
Рисунок 4 – Зависимость величины относительной суммарной длины линий связи от числа ступеней

Анализируя график на рисунке 4, приходим к выводу, что увеличение числа ступеней, то есть степени ветвления иерархической структуры позволяет существенно сократить суммарную длину линий связи, то есть приводит к более эффективному и экономически выгодному соединению объектов. Но следует помнить, что чрезмерное увеличение количества ступеней отрицательно скажется на надёжности функционирования системы, поэтому основной проблемой в выборе оптимальной степени ветвления структуры является поиск компромисса между экономическими показателями и требованиями по надёжности.