2. Программирование сложных однооузловых ветвлений

Рассмотренные варианты ветвящихся процессов использовали проверку одного или нескольких взаимоисключающих условий, что приводило к получению в алгоритмах и программах двух и более последовательно формируемых вычислительных ветвей.

При этом проверяемые условия оформлялись любыми комбинациями логической проверки ( <, >, , , =, ).

В некоторых реальных задачах требуется проверка специфических условий, когда выбор конкретной ветви определяется проверкой на равенство целочисленной константе. При этом количество создаваемых ветвей, а, следовательно, и проверяемых условий (констант) может изменяться в значительном диапазоне, начиная с 2 и заканчивая десятками.

Графическая интерпретация сложного узла определяет одну исходную и некоторое количество выходных ветвей:

Р ассмотрим программирование сложного одноузлового ветвления на задаче (4.4) о размере стипендии.

Постановка задачи

Рассчитать размер стипендии, выплачиваемой студентам, если известно, что не явившиеся на экзамен, получившие «неудовлетворительно» и «удовлетворительно» стипендию не получают, сдавшие на «хорошо» получают базовую стипендию, сдавшие на «отлично» – повышенную.

Формирование математической модели

Исходные данные

Баз = _ _ р. – размер базовой стипендии;

k = _,_ _ – коэффициент повышения стипендии;

Балл = _ – полученный балл;

Расчётные зависимости

Первый вариант:

размер стипендии, [р.]

Второй вариант:

размер

стипендии,

[р.]

Т

размер

стипендии,

[р.]

ретий вариант:

Выбор метода решения

Анализ полученных математических моделей позволяет констатировать:

• Первая из формулировок соответствует последовательной проверке на пять целочисленных констант (= 0, = 2, = 3, = 4, = 5). Она предписывает многократную одноузловую проверку.

• Вторая объединяет все возможные варианты ниже «хорошо» в одно составное условие.

• Третья соответствует традиционной форме сложного (двухузлового) ветвления на два, преобразуя множественную проверку на одну из целочисленных констант в два взаимоисключающих условия. Главное 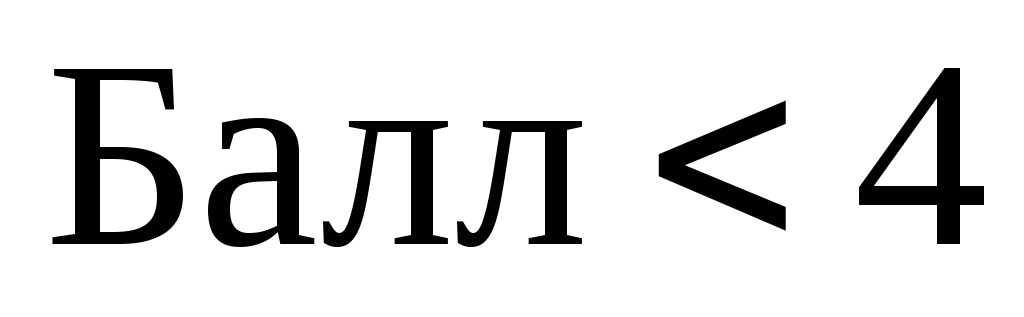(), действующее на все три ветви и дополнительное (), действующее только в ветви , взаимоисключающей главное.

Следовательно, в качестве метода решения:

• первая математическая модель требует разветвляющегося вычислительного процесса с одноузловым множественным ветвлением на пять;

• вторая предписывает ветвящийся вычислительный процесс с одноузловым множественным ветвлением на три;

• третья определяет стандартное двухузловое, с указанными в модели зависимостями, последовательное ветвление на два.

Составление алгоритма решения

Алгоритмизация по первому и второму вариантам математической формулировки требует использования специфической структуры «множественный выбор» (см. разд. 2.6). С учетом этого схемы алгоритмов представлены на рис. 4.11 а, 4.11 б. Схема алгоритма по третьему варианту реализована рис. 4.12.

Наличие в алгоритмах ряда параллельно расположенных блоков (4-8 рис. 4.11 а, 4-6 рис. 4.11 б, 5-7 рис. 4.12) требует преобразования их в условно-линейные (рис. 4.13).

Программирование задачи

Алгоритм организации ветвления типа «выбор» со значительным числом ветвей в зависимости от значения проверяемого целочисленного операнда (выражения) реализуется в Си/Си++ специальной конструкцией из двух операторов – переключателя (switch) и разрыва (break).

Структура конструкции:

switch(выражение)

{

case n1:

оператор 1;

[break;]

. . .

case ni:

оператор i;

[break;]

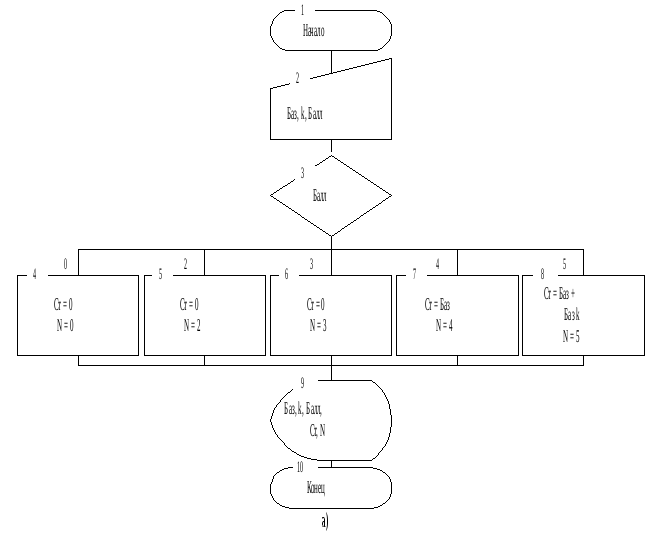
Рис. 4.11. Схемы алгоритмов задачи 4.4 с множественным ветвлением

Рис. 4.12. Схема алгоритма задачи 4.4 с последовательным ветвлением на два

Рис. 4.13. Варианты условно линейных схем алгоритмов

. . .

case nN:

оператор N;

[break;]

[default:

оператор N+1;]

}

где switch –ключевое слово, название основного оператора (переключатель);

выражение – любое с целочисленным результатом;

( ) – ограничители выражения;

case –ключевое слово (вариант);

n1 ni nN – целая константа (метка), обозначающая требуемый вариант (начиная с нуля);

: – признак метки;

оператор i; –один из простых операторов, соответствующих каждому варианту выбора;

default –ключевое слово (по умолчанию);

{ } – ограничители тела оператора switch;

[ ] – признак необязательности содержимого;

break – вспомогательный оператор (разорвать, выйти).

Оператор работает следующим образом:

• вычисляется значение выражения переключения. Результат – целая (символьная) константа;

• результат последовательно сравнивается с каждой из меток ni в диапазоне от n1 до nN;

• если совпадение с одной из меток ni произошло, выполняется соответствующий оператор (i) и оператор break, если он имеется, передает управление оператору программы, расположенному под закрывающей фигурной скобкой. (При отсутствии оператора break после оператора i сохраняется естественный порядок выполнения ниже записанных операторов, начиная с (i+1));

• если метки ni, аналогичной результату вычисления выражения не обнаружено и элемент по умолчанию (default: оператор N+1;) присутствует, управление передается оператору N+1, а затем оператору, расположенному под закрывающей фигурной скобкой.

При отсутствии элемента по умолчанию управление напрямую передается оператору под фигурной скобкой.

Так, фрагменты программ

int i; . . . switch( i ) { case 1: x=1; break; case 2: y=7; break; case 6: z=15; break; default: t=0; } s=3;

int i; . . . switch( i ) { case 1: x=1; break; case 2: y=7; break; case 6: z=15; break; } s=3;

предписывают вычисление х, если i = 1, вычисление у, если i = 2, вычисление z при i = 6, а затем передачу управления на вычисление переменной s. Если же i 1, 2, 6, то в левом фрагменте будут вычислены t и s, а в правом фрагменте – только s.