1. Программирование сложных многоузловых ветвлений

Типичный пример реализации – ветвление на три (проверка на равно, больше, меньше), используемое в большинстве реальных вычислительных задач. Выполним предмашинную подготовку одной из них – задачи (4.3) о расчете расхода бензина.

Постановка задачи

Рассчитать объём бензина, необходимый для пятиминутного движения автомобиля с постоянной скоростью, если известно, что расход зависит от скорости движения:

• при V = 80 км/ч (оптимальная скорость), расход 7,6 л/ч;

• при V < 80 км/ч, расход на 4,3 % больше;

• при V > 80 км/ч, расход на 8 % больше.

Формирование математической модели

Исходные данные

t = _ _ мин – время движения;

V = _ _,_ км/ч – скорость движения;

V_опт = _ _,_ км/ч – оптимальная скорость;

P_боч = _,_ л/ч – оптимальный расход бензина в час;

Пр₁ = _,_ % – увеличение расхода при V<80 км/ч;

Пр₂ = _,_ % – увеличение расхода при V>80 км/ч.

Расчётные зависимости

объём требуемого бензина при движении с постоянной оптимальной скоростью;

Искомый расход бензина при движении с заданной скоростью:

Полученная математическая формулировка соответствует одновременной проверке на = и < , >, что допустимо в математике, но нестандартно (непригодно) для программирования. Поэтому её необходимо преобразовать в универсальную с последовательным ветвлением на два:

В полученной записи вместо одного нестандартного записаны два взаимоисключающих условия. Главное, действующее на все три ветви V = V_опт (), и одно дополнительное V>V_опт (V<V_опт), действующее только в ветви .

Для увеличения дружественности математической модели дополним полученные зависимости (ветви) обозначениями их порядковых номеров (n = 1, n = 2, n = 3).

Таким образом, математическая модель принимает откорректированный вид:

Выбор метода решения

Полученные математические формулировки позволяют сделать вывод:

• первая из них требует разветвляющегося вычислительного процесса с нестандартной схемой решения, и реализации не подлежит;

• вторая определяет возможность расчета расхода бензина по трем формулам (ветвям), обусловленным проверкой двух условий: главного (V = V_опт), а затем, если оно не выполнено (), второго – вспомогательного V<V_опт, что соответствует универсальной схеме ветвления на два, но не содержит элементов обозначения номеров ветвей;

• третья сохраняет все достоинства предыдущей (последовательное ветвление на два с достаточно простыми главным и вспомогательным условиями) и дополнена элементами дружественности.

Следовательно, в качестве метода решения желательно выбрать сложный разветвляющийся вычислительный процесс последовательной проверки одного главного и одного дополнительного условий, реализующий три возможных пронумерованных вычислительных ветви.

Составление алгоритма решения

Окончательный вариант математической формулировки и выбранный метод решения позволяют создать одношаговую схему алгоритма решения задачи 4.3, представленную на рис. 4.9.

Созданная структура двойного последовательного ветвления при необходимом изменении содержимого вычислительных блоков может использоваться при решении любых задач, в которых требуется проверка двух взаимоисключающих условий, одно из которых – главное.

Алгоритм, как стандартный, содержит ряд параллельно расположенных блоков (7–12). Для возможности последующего программирования преобразуем его в две условно-линейные схемы (рис. 4.10).

В левой схеме естественный порядок выполнения блоков соответствует ветвям «НЕТ», а в правой – ветвям «ДА».

Рис. 4.9 Основная схема алгоритма задачи 4.3.

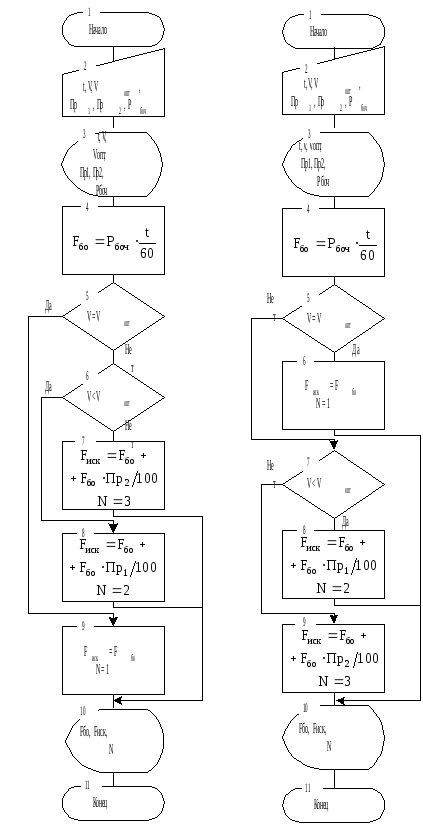
Рис. 4.10 Условно-линейные варианты схем алгоритма