Тема: Периодические дроби.
1. Представьте следующие рациональные числа в виде десятичных дробей:
а) 
; б) 
; в) 
; г) 
.
Сложность: 2
Классы: 6,7,8
Ответ
а)
=
0,(142857);
б)
=
0,(285714);
в)
=
0,(714285);
г)
=
0,(0588235294117647).
2. Докажите, что бесконечная десятичная дробь 0,1234567891011121314... (после запятой подряд выписаны все натуральные числа по порядку) представляет собой иррациональное число. Сложность: 2+ Классы: 8,9
Подсказка
В этой дроби любая конечная последовательность цифр встретится сколь угодно далеко от запятой.
Решение
Как известно, рациональные числа выражаются десятичными дробями, которые имеют период начиная с некоторого знака. Поэтому достаточно доказать, что данная дробь не является периодической ни с какого знака. Предположим, что это не так, и некоторая последовательность T, состоящая из n цифр, является периодом дроби начиная с m-го знака после запятой. Ясно, что среди цифр после m-го знака встречаются ненулевые, поэтому в последовательности цифр T есть ненулевая цифра. Это означает, что начиная с m-ой цифры после запятой, среди любых n цифр подряд есть ненулевая цифра. Однако в десятичной записи данной дроби должна присутствовать десятичная запись числа 100...0=10k, где k больше m и n. Понятно, что эта запись встретится правее m-ой цифры и содержит более n нулей подряд. Тем самым, получаем противоречие, завершающее доказательство.
3. Докажите, что дроби 1000/2001 и 1001/2001 имеют равную длину периодов. Сложность: 2+ Классы: 8,9
Подсказка
1=0,999999...
Решение
Заметим, что сумма двух данных дробей равна 1. Пусть первая дробь имеет десятичную запись 1000/2001 = 0,a1a2a3... Рассмотрим число R, выраженное десятичной дробью, меньшей 1, у которой на i-ом месте после запятой, стоит цифра (9-ai). Тогда в сумме 1000/2001+R в каждом разряде после запятой будет стоять 9, т.е. 1000/2001+R=0,9999..., что равно 1. Таким образом, R=1001/2001. Теперь видно, что если ab...z - некоторая комбинация цифр, являющаяся периодом дроби 1000/2001, то комбинация цифр (9-a)(9-b)...(9-z) есть период дроби 1001/2001. Следовательно, период дроби 1001/2001 не длиннее периода 1000/2001. Аналогично показываем, что период дроби 1000/2001 не длиннее период дроби 1001/2001. Тем самым, показано, что периоды двух данных дробей равны.
4. Найдите цифры a и b такие, для которых
=
0, bbbbb...
Сложность: 3
Классы: 8,9
Ответ
a = 0, b = 0 или a = 1, b = 3.
5. Найдите возможные значения знаменателя обычной дроби вида 1/m, которая представляется чисто периодической десятичной дробью с двумя цифрами в периоде. Сложность: 3 Классы: 8,9,10
Ответ
11, 33 и 99 — делители числа 99, не делящие 9.
6. Докажите, что равенство
=
равносильно тому, что
десятичное представление дроби
имеет
вид
=
0,(a1a2...an).
Сложность: 3+
Классы: 8,9,10
Решение
По формуле для суммы геометрической прогрессии
0,(a1...an)
=
.
Отсюда, если
=
,
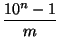то
=
0,(a1a2...an).
7. Число 1/42 разложили в бесконечную десятичную дробь. Затем вычеркнули 1997-ю цифру после запятой, а все цифры, стоящие справа от вычеркнутой цифры, сдвинули на 1 влево. Какое число больше: новое или первоначальное? Сложность: 3+ Классы: 8,9,10
Решение
Число 1/42 можно представить в виде периодической десятичной дроби. Период начинается со второй цифры после запятой (двойки) и состоит из 6 цифр: 238095 (1/42 = 0,0238095238...). Установить это можно, например, с помощью деления 1 на 42 "столбиком". Поскольку 1997 при делении на 6 даёт остаток 5, 1997-я цифра записанного числа та же, что и пятая — нуль, а следующая — девятка. Значит, новое число больше. Бесконечные периодические десятичные дроби обозначаются так: 1/42 = 0,0(238095).
8. Представьте следующие числа в виде обычных и в виде десятичных дробей:
а) 0,(12) + 0,(122); б) 0,(3) . 0,(4); в) 0,(9) - 0,(85). Сложность: 3+ Классы: 7,8,9
Ответ
а) 15926/111111 = 0,(143334); б) 4/27 = 0,(148); в) 14/99 = 0,(14).
9. Докажите, что если (m, 10) = 1, то у десятичного представления дроби 1/m нет предпериода. Сложность: 3+ Классы: 8,9,10