5.4.3. Альтернативи, що чітко не домінуються, та їх властивості

У цьому розділі ми розглядаємо задачі, у яких множина альтернатив, що недомінуються є нормальною нечіткою підмножиною X, тобто функція належності цієї підмножини має властивість

(5.26)

У цьому випадку для нашої альтернативи з множини максимальних недомінуємих альтернатив виконано тобто міра недомінуємості для кожної такої альтернативи дорівнює 1.

Іншими словами, для кожної і будь-якої при цьому виконується рівність тобто жодна альтернатива не домінує з позитивним ступенем подану альтернативу x.

Тому ці альтернативи ми будемо називати чітко недомінуємими, й множину таких альтернатив позначимо X ^ЧНД. Таким чином

Х ^ЧНД. (5.27)

Як випливає з визначення множини Х^ЧНД та , для кожної чітко недомінованої альтернативи виконується рівність

Х ^ЧНД , (5.28)

де – нечітке відношення строгої переваги, що відповідає . Звідси можна зробити висновок, що для будь-яких  Х ^ЧНД виконується

. (5.29)

Із визначення випливає, що рівність (5.29) еквівалентна рівності

,

але тоді

,

тобто будь-які дві альтернативи, що чітко недомінуюються пов'язані відношенням байдужості зі ступенем не меншим за 0,5. За визначенням нечіткого відношення отримуємо

Х ^ЧНД . (5.30)

При довільних нечітких відношеннях переваги може виявитися, що , при  Х ^ЧНД, тобто альтернативи можуть не бути еквівалентними ні з якою позитивною мірою. Зауважимо, що в цьому випадку , тобто та не зрівняні мiж собою. Однак це не має місця, якщо лінійне відношення.

5.5. Декілька відношень переваги на множині альтернатив

Розглянемо таку задачу. Нехай задана множина альтернатив X і кожна альтернатива характеризується декількома ознаками з номерами Інформація про попарне порівняння альтернатив подана у вигляді відношень переваги , Таким чином, ми маємо m відношень переваги на множині X. Задача полягає в тому, щоб за даною інформацією зробити раціональний вибір альтернатив з множини

Звернемося спочатку до ситуації, коли відношення описуються числовими функціями корисності де – числова вісь. Значення функції можна вважати числовою оцінкою альтернативи за ознакою j, . Перевага за ознакою j віддається альтернативі з більш високою оцінкою . Задача полягає в тому, щоб вибрати альтернативу, яка має якомога більші оцінки за всіма ознаками. Раціональними в цьому випадку природно вважати вибір альтернативи , яка має таку властивість:

якщо , то . (5.31)

Такі альтернативи у багатокритеріальній оптимізації звуться ефективними.

Легко бачити, що кожна функція , описує звичайне відношення переваги на множині альтернатив таким чином

(5.32)

Hехай Покажемо, що множина всіх ефективних (недомінуємих) альтернатив у множині співпадає з множиною ефективних альтернатив для набору функцій

Hехай – альтернатива, що не домінується в множині . Це означає, що для будь-якого виконується

(5.33)

де – відповідне до відношення строгої переваги, воно має вигляд

. (5.34)

Звідси і з (5.33) отримуємо (5.31), тобто – ефективна альтернатива для функції

Можна показати і зворотне, тобто, що будь-яка альтернатива для функцій не домінується у множині . Таким чином, для того, щоб знайти множину ефективних альтернатив, можна замість набору відношень , взяти переріз цих відношень i знайти множину недомінуємих альтернатив в множині . Запишемо тепер переріз відношень у іншому вигляді.

Hехай

(5.35)

– функція належності . Тоді перерізу цих відношень відповідає функція належності

, (5.36)

яка є аналогом згортки критеріїв у багатокритеріальних задачах прийняття рішень. Тут числа – коефіцієнти відносної важливості критеріїв. У згортці (5.36) що відповідає тому, що всі подані відношення однаково важливо враховувати при виборі альтернатив. Якщо подані відношення відрізняються лише за важливістю відповідних ознак, за якими порівнюються альтернативи, то у згортці (5.36) можна використовувати різні за величиною коефіцієнти . При цьому вихідні відношення ми повинні розглядати, як нечіткі, тобто в визначенні функції належності (5.35) числа 0 та 1 необхідно розуміти, як крайні точки одиничного інтервалу можливих значень степені належності.

У результаті згортки вихідних відношень з коефіцієнтами такими, що отримуємо функцію належності, що має вигляд

, (5.37)

тобто функцію належності нечіткого відношення переваги. Але це відношення не буде рефлексивним, це означає, що воно не є відношенням переваги у сенсі визначення пункту, і цю згортку незручно застосовувати, коли необхідно враховувати вагу поданих відношень.

Тому введемо тепер згортку вихідних відношень іншого вигляду.

. (5.38)

Зауважимо, що отримане після згортки (5.38) звичайних відношень нечітке відношення буде рефлексивним, тому що рефлексивними є вихідні відношення.

Нехай усі вихідні відношення переваги однакові за важливістю. У (5.38) це відповідає тому, що Визначимо підмножину альтернатив, що не домінуються на множині , використовуючи визначення пункту 5.4.2.

(5.39)

Позначимо Х₁^ЧНД підмножину чітко недомінуємих альтернатив у множині , а Х₂^ЧНД – відповідна підмножина в . Покажемо, що Х₂^ЧНД  Х₁^ЧНД Дійсно, нехай  Х₂^ЧНД . Згідно з визначенням чітко недомінуємої альтернативи та (5.39) це означає, що

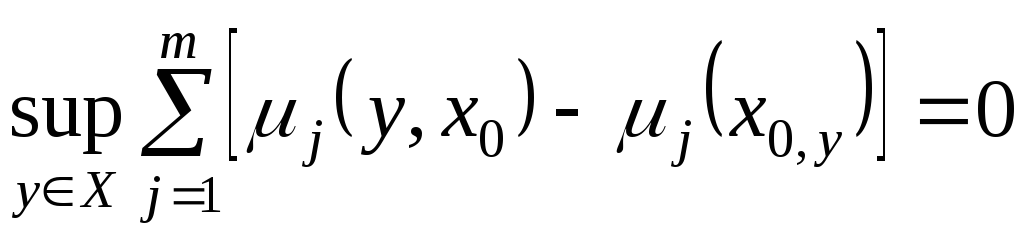
або

(5.40)

для будь-яких Припустимо, що Х₁^ЧНД Тоді, відповідно (5.31) і (5.35) отримаємо, що знайдеться такий , що і для деякого виконується Але тоді для альтернативи y не вірно (5.51). Звідти отримуємо, що Х₁^ЧНД , тобто Х₂^ЧНД  Х₁^ЧНД

З а у в а ж е н н я. Множина Х₂^ЧНД не включає в себе всі ефективні альтернативи для функцій , тобто не співпадає з множиною Х₁^ЧНД, але можна показати, що кожна ефективна альтернатива, тобто кожний елемент Х₁ ^ЧНД належить до множини з позитивним ступенем,

Х₁^ЧНД .

Дійсно, якщо для будь-якої альтернативи виконано , то з (5.39) отримуємо, що відшукається для якого

тобто i для всiх j = 1, … , m. Це означає, що альтернатива у домінує альтернативу х, тобто , j = 1, ... , m й очевидно х не може бути ефективною альтернативою для набору функції .

Функція впорядковує альтернативи за ступенем їх недомінуємості. Наприклад, якщо і яка-небудь альтернатива строго краще альтернативи х за якими-небудь двома ознаками, то не менш чим за однією ознакою із тих, що залишилися альтернатива х строго переважає альтернативу у.

Якщо взяти переріз множин Х₁^ЧНД й , то отримаємо відповідне впорядкування на множині ефективних альтернатив, користуючись яким можна здійснити вибір серед них.

Таким чином, застосування згортки (5.38) вихідних звичайних відношень у задачі прийняття рішень на наборі функцій дозволяє одержати додаткову інформацію про відносний степінь недомінуємості ефективних альтернатив і тим звузити клас раціональних виборів до множини

У загальній задачі, коли на множині альтернатив задано m нечітких відношень переваги , j = 1, ... , m і задано коефіцієнти , j = 1, ... , m відносної ваги цих відношень, можна діяти таким же чином.

Сформулюємо алгоритм вибору при декількох заданих на множині альтернатив відношеннях переваги.

1. Будуємо нечітке відношення (переріз вихідних відношень):

.

та визначаємо нечітку підмножину недомінуємих альтернатив в множині :

.

2. Будується нечітке відношення Q₂ (згортка відношень типу (5.38)):

.

і визначаємо нечітку підмножину недомінуємих альтернатив у множині :

.

3. Знаходимо переріз множин та : .

4. Раціональним вважаємо вибори альтернатив із множини

^.

Тут слід зауважити, що залежно від типу задачі, раціональними можна вважати не тільки альтернативи з множини Х^.Н.Д., але в тому чи іншому сенсі й слабко домінуємі альтернативи (або не дуже сильно домінуємі альтернативи), тобто альтернативи, які належать до множини ^.н.д. зі ступенем не нижчим деякого поданого.

П р и к л а д 5.6. Нехай , на Х подані три відношення переваги (чіткі), що мають однакову вагу.

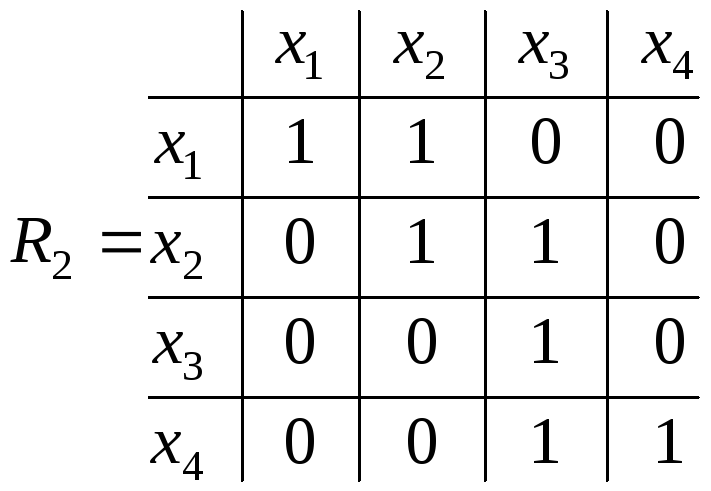
Здійснити раціональний вибір альтернативи з Х на основі поданих відношень переваги.

Розв’язування

Оскільки відношення переваги мають однакову вагу коефіцієнти , j = 1, ... , m відносної ваги приймемо рівними .

1. Будуємо відношення

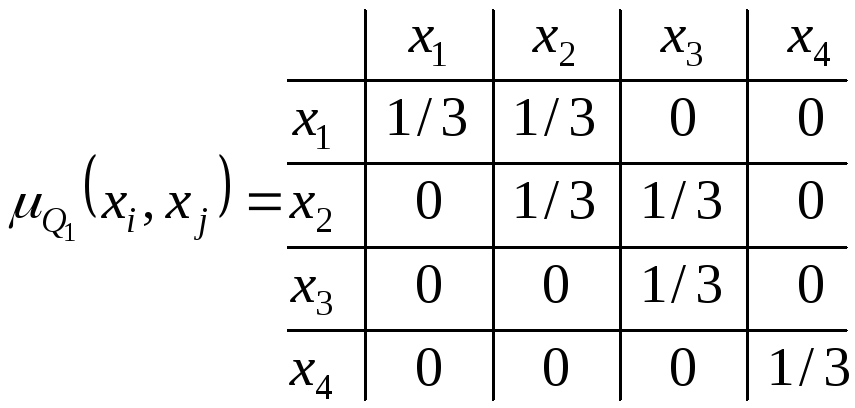
Знаходимо відношення строгої переваги

і знаходимо підмножину альтернатив, що недомінуються в множині

.

2. Будуємо відношення :

,

відповідне йому відношення строгої переваги:

,

Знаходимо підмножину альтернатив, що недомінуються у множині

.

3. Множина недомінуємих альтернатив є переріз множин та

.

Звідсіля одержуємо, що у поданому прикладі раціональним слід вважати вибір альтернативи х₁ та х₂, які мають максимальний степінь недомінуємості.

П р и к л а д 5.7. Нехай на множині подано два нечіткі відношення переваги R₁ та R₂, причому перше з цих відношень має вагу вдвічі більшу за друге.

,

Здійснити раціональний вибір альтернативи з Х на основі поданих відношень переваги.

Розв’язування

1. Будуємо відношення

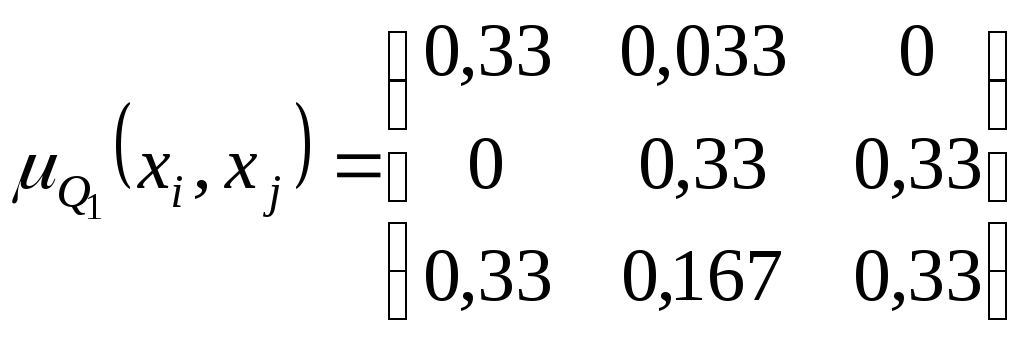
відповідне йому відношення строгої переваги:

,

й знаходимо підмножину недомінуємих альтернатив в множині

.

2. Будуємо відношення

,

відповідне відношення строгої переваги:

.

і знаходимо підмножину недомінуємих альтернатив у множині

.

Вихідна множина недомінуємих альтернатив

.

Максимальну степінь недомінуємості має альтернатива х₂, тому вибір її можна вважати раціональним.