Параграф 5: последовательность. Точка. Предел последовательности.

Опр. 1: Последовательностью называется множество чисел, пронумерованных с помощью чисел и расположенных в порядке возрастания номеров.

– общий член последовательности.

N – номер члена последовательности, играет роль аргумента функции. Фактически задает последовательность целочисленных аргументов.

– функция целочисленных аргументов.

Выражение примеров последовательности:

ПРИМЕРЫ:

1. – общий член последовательности.

;

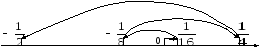2.

Будем различать последовательности, имеющие предел, и не имеющие предела. Общий член последовательности – переменная величина, значение которого определяется номером N. Эта величина является функцией аргумента N

Параграф 6: предел последовательности.

Опр. 1: Постоянное число называется пределом переменной, если для любого сколь угодно малого числа , существует такой номер , что при выполнении неравенства следует выполнение неравенства:

В силу леммы о вещественных числах (№1) одно неравенство с модулем (1) равносильно двойному неравенству:

Неравенство (2) определяет на оси E так называемую E – окрестность точки a.

Неравенство (2) означает, что переменная точка находится в E – окрестности точки a.

Постоянное число a называется пределом переменной , если для любой сколь угодно малой E – окрестности точки a начиная с некоторого номера n (n > N), точка попадает в эту E – окрестность, и при своем дальнейшем изменении будет там находиться.

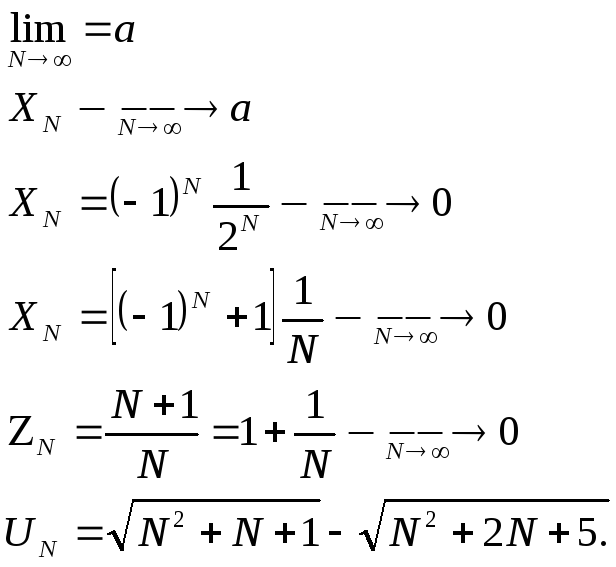
Limit – предел.

Параграф 7: бесконечно малые величины.

Опр. 1: Переменная называется бесконечно малой, если её пределом является нуль.

Определение на языке : Переменная называется бесконечно малой, если для любого E > 0 существует такой номер N, что при выполнении неравенства n > N, следует выполнение неравенства:

ПРИМЕРЫ:

1.

2.

3. – не имеет предела.

ЛЕММЫ О БЕСКОНЕЧНО МАЛЫХ ВЕЛИЧИНАХ.

ЛЕММА №1:

Для того чтобы переменная имела своим пределом постоянное число a, необходимо и достаточно выполнения равенства:

– бесконечно малая величина.

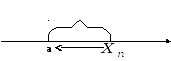
Результат следует из того, что разность есть расстояние от точки до её предела , это расстояние стремится к нулю, т. к. , и наоборот: если расстояние стремиться к нулю, то .

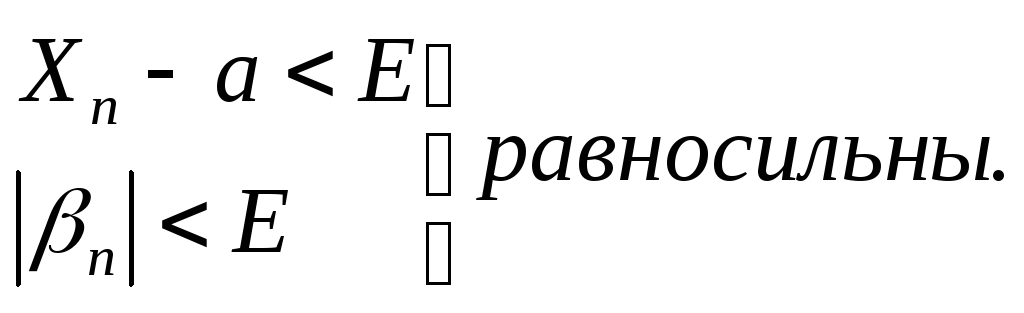
ЛЕММА №2:

Алгебраическая сумма конечного числа бесконечно малых, есть величина бесконечно малая.

Доказательство:

Рассмотрим, например, сумму 3-х бесконечно малых.

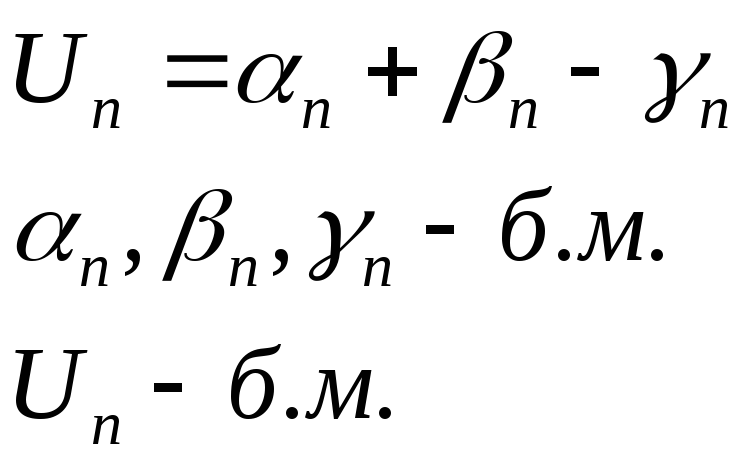
Возьмем любое E > 0, т. к. ,то по определению существует номер n такой, что будет выполняться три неравенства:

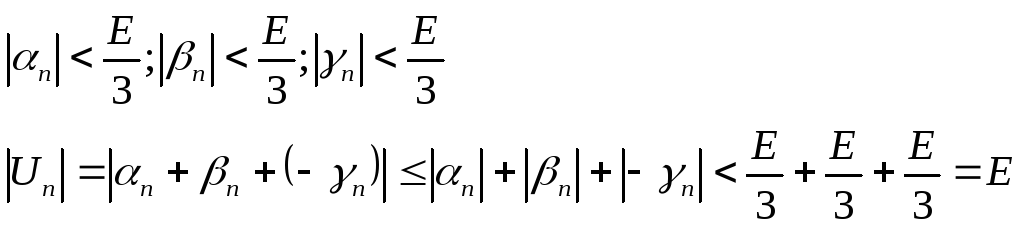
(по лемме №2 о вещественных числах).

Существует номер n, такой, что при n > N выполняется неравенство:

для , это и означает, что , Ч. Т. Д.

Опр. 2: Переменная называется ограниченной, если существуют такие m и M , что для всех выполняется равенство:

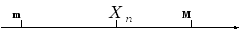
ПРИМЕР:

1. Sin n – ограниченное, т. к. |sin n| ≤ 1.

2. 

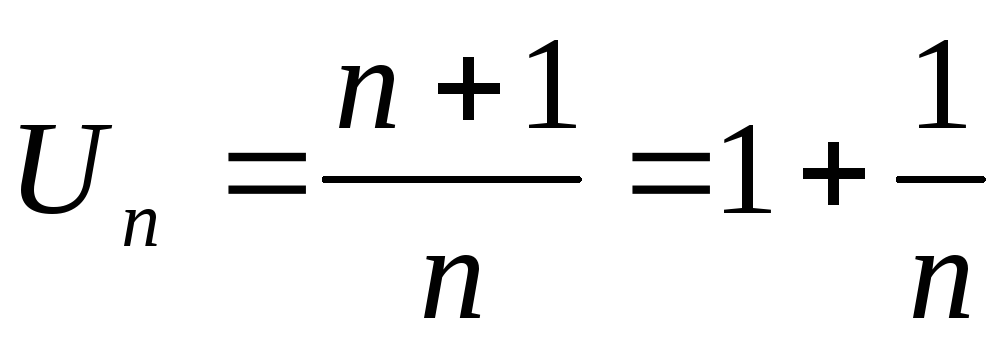
3. – не является ограниченным.

(О. П. – ограниченная переменная).

ЛЕММА №3:

Произведение о. п. на б. м. есть величина б. м.

Пусть

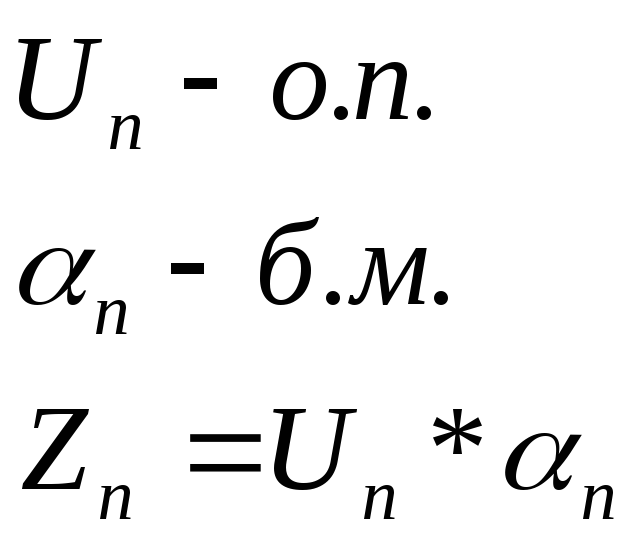
Требуется доказать, что:

Доказательство:

Пусть

Возьмем , т.к. – бесконечно малая, то существует номер N такой что при: ,

Тогда .

, при , следовательно, выполняется неравенства:

,

Это и означает, что: – бесконечно малая.