Тесты 2-го блока сложности

1. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=1; y₀ = 1; ), равен…

   1. 0.25 ; *

   2. 0.5 ;

   3. 0.125;

   4. нет правильного ответа.

2. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=1; y₀ = 1; ), равен…

   1. 0.125; *

   2. 0.25 ;

   3. 0.5;

   4. нет правильного ответа.

3. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=1; y₀ = 1; ), равен…

   1. 0.0625; *

   2. 0.5;

   3. 0.25;

   4. нет правильного ответа.

4. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=1; y₀ = 1; ), равен…

   1. 0.0625 ; *

   2. 0.125;

   3. 0.5;

   4. нет правильного ответа.

5. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=1; y₀ = 1; ), равен…

   1. 0.0625; *

   2. 0.5;

   3. 0.125;

   4. нет правильного ответа.

6. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=1; y₀ = 1; ), равен…

   1. 0.125; *

   2. 0.25 ;

   3. 0.0625;

   4. нет правильного ответа.

7. Формула для вычисления шага спуска () при вычислении минимума функции методом НСА, имеет вид…

1. ; *

2. ;

3. ;

4. .

8. Формула для вычисления шага спуска () при вычислении минимума функции методом НСА, имеет вид…

   1. ; *

   2. ;

   3. ;

   4. .

9. Формула для вычисления шага спуска () при вычислении минимума функции методом НСА, имеет вид…

   1. ; *

   2. ;

   3. ;

   4. .

10. Формула для вычисления шага спуска () при вычислении минимума функции методом НСА, имеет вид…

    1. ; *

    2. ;

    3. ;

    4. .

11. Формула для вычисления шага спуска () при вычислении минимума функции методом НСА, имеет вид…

    1. ; *

    2. ;

    3. ;

    4. .

12. Координаты точки минимума функции , найденные аналитическим методом минимум, равны ...

    1. [-0.25,2] ; *

    2. [0,0] ;

    3. [1,2] ;

    4. функция не имеет минимума.

13. Координаты точки минимума функции , найденные аналитическим методом минимум, равны ...

    1. [0.25,0] ; *

    2. [0,0.25] ;

    3. [1,0] ;

    4. функция не имеет минимума.

14. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции методом ГДШ (х₀=1; y₀ = 1; ), равен…

    1. ; *

    2. ;

    3. ;

    4. .

15. Координаты точки минимума функции , найденные аналитическим методом минимум, равны ...

    1. [-0.25,0] ; *

    2. [0,0] ;

    3. [1,0] ;

    4. функция не имеет минимума.

16. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=1; y₀ = 3; ), равен…

    1. ; *

    2. ;

    3. ;

    4. .

17. Координаты точки минимума функции , найденные аналитическим методом минимум, равны ...

    1. функция не имеет минимума ; *

    2. [-0.5,0.25];

    3. [1,0];

    4. [0.5,0.25].

18. Координаты точки [х₁ ; y₁] при вычислении точки функции методом ГДШ (х₀=1; y₀ = 3; ), равны…

    1. 0.125; *

    2. 0.0625;

    3. 0.5;

    4. нет правильного ответа.

19. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=2; y₀ = ; 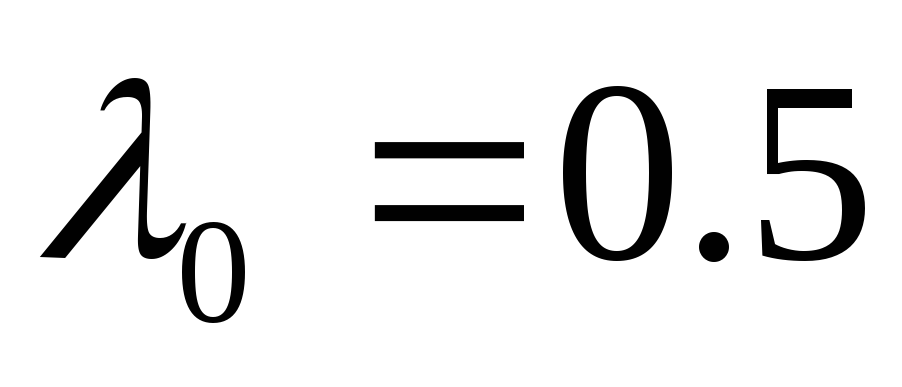), равен…

    1. 0.25; *

    2. 0.5;

    3. 0.125;

    4. нет правильного ответа.

20. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=2; y₀ = 1; ), равен…

    1. 0.25; *

    2. 0.125;

    3. 0.5;

    4. нет правильного ответа.

21. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=2; y₀ = 0; ), равен…

    1. 0.25; *

    2. 0.5;

    3. 0.0625;

    4. нет правильного ответа.

22. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=1; y₀ = 1; ), равен…

    1. 0.25 ; *

    2. 0.125;

    3. 0.065;

    4. нет правильного ответа.

23. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=1; y₀ = 1; ), равен…

    1. 0.0625; *

    2. 0.5;

    3. 0.125;

    4. нет правильного ответа.

24. Шаг спуска, обеспечивающий условие метода ГДШ, для вычисления координаты точки [х₁;y₁] для функции (х₀=1; y₀ = 1; ), равен…

    1. 0.125; *

    2. 0.25 ;

    3. 0.0625;

    4. нет правильного ответа.

25. Координаты точки минимума функции , найденные аналитическим методом минимум, равны ...

    1. функция не имеет минимума ; *

    2. [-0.5,0.25] ;

    3. [1,0] ;

    4. [0.5,0.25].