
- •Тестовые задания по теме «Методы решения обыкновенных дифференциальных уравнений» Тесты 1-го блока сложности
- •Тесты 2-го блока сложности
- •Тесты 3-го блока сложности
- •Тестовые задания по теме «Одномерная оптимизация» Тесты 1-го блока сложности
- •Тесты 2-го блока сложности
- •Тесты 3-го блока сложности
- •Тестовые задания по теме «Методы оптимизации функции нескольких переменных» Тесты 1-го блока сложности
- •Тесты 2-го блока сложности
- •Тесты 3-го блока сложности
- •Тестовые задачи по теме «Обыкновенные дифференциальные уравнения» Тесты 1-го блока сложности
- •Тесты 2-го блока сложности
- •Тестовые задачи по теме «Многомерная оптимизация» Тесты 1-го блока сложности
- •Тесты 2-го блока сложности
- •Тестовые задачи по теме «Одномерная оптимизация» Тесты 1-го блока сложности
- •Тесты 2-го блока сложности
На отрезке [a;b] имеется хотя бы
один корень, если
![]() --------------------------------------------
Оценка
погрешности значения интеграла
--------------------------------------------
Оценка
погрешности значения интеграла
 по
правилу Рунге, вычисленного по методу
трапеций
с h=0.2 и h=0.1, по правилу Рунге
составляет
0.0058
--------------------------------------------
Задача
нахождения корня нелинейного уравнения
с заданной точностью
по
правилу Рунге, вычисленного по методу
трапеций
с h=0.2 и h=0.1, по правилу Рунге
составляет
0.0058
--------------------------------------------
Задача
нахождения корня нелинейного уравнения
с заданной точностью
![]() считается
решенной, если
считается
решенной, если
![]() --------------------------------------------
Чтобы
выбрать x0 в качестве
начального приближения в методе Ньютона
необходимо, чтобы в этой точке
функция
и вторая производная имели одинаковые
знаки
--------------------------------------------
Этап
«отделения корней» нелинейного уравнения
заключается в
нахождении отрезков,
внутри которых находится строго один
корень
--------------------------------------------
Этапы
решения нелинейного уравнения называются
отделение корней и уточнение отделенного
корня
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу правых
прямоугольников с h=0.2 и h=0.1, если функция
задана таблично,
по правилу Рунге
составляет
--------------------------------------------
Чтобы
выбрать x0 в качестве
начального приближения в методе Ньютона
необходимо, чтобы в этой точке
функция
и вторая производная имели одинаковые
знаки
--------------------------------------------
Этап
«отделения корней» нелинейного уравнения
заключается в
нахождении отрезков,
внутри которых находится строго один
корень
--------------------------------------------
Этапы
решения нелинейного уравнения называются
отделение корней и уточнение отделенного
корня
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу правых
прямоугольников с h=0.2 и h=0.1, если функция
задана таблично,
по правилу Рунге
составляет
![]() 0.15
--------------------------------------------
Оценка
погрешности значения интеграла
0.15
--------------------------------------------
Оценка
погрешности значения интеграла
 ,
вычисленного по методу Симпсона с h=2 и
h=1,
по правилу Рунге составляет
0.005
--------------------------------------------
Начальное
приближение к корню при решении
нелинейного уравнения
,
вычисленного по методу Симпсона с h=2 и
h=1,
по правилу Рунге составляет
0.005
--------------------------------------------
Начальное
приближение к корню при решении
нелинейного уравнения![]()
![]() методом
итерации служит
любое значение
методом
итерации служит
любое значение
![]() --------------------------------------------
Количество
интервалов разбиения, кратное двум,
необходимо выбирать для вычисления
интеграла
методом
Симпсона
--------------------------------------------
Оценка
погрешности значения интеграла
--------------------------------------------
Количество
интервалов разбиения, кратное двум,
необходимо выбирать для вычисления
интеграла
методом
Симпсона
--------------------------------------------
Оценка
погрешности значения интеграла
 ,
вычисленного по методу трапеций с h=2 и
h=1,
по правилу Рунге составляет
0.139
--------------------------------------------
Формула
погрешности
,
вычисленного по методу трапеций с h=2 и
h=1,
по правилу Рунге составляет
0.139
--------------------------------------------
Формула
погрешности
![]() ,
где
,
где
![]() применятся
в
методе средних
прямоугольников
--------------------------------------------
В
процессе решения нелинейного уравнения
методом простой итерации приближение
к корню может осуществляться
монотонно
или колебательно
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
применятся
в
методе средних
прямоугольников
--------------------------------------------
В
процессе решения нелинейного уравнения
методом простой итерации приближение
к корню может осуществляться
монотонно
или колебательно
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
![]() для
функции, заданной таблично,
значение
в точке х=4,6 равно
для
функции, заданной таблично,
значение
в точке х=4,6 равно
![]()
![]() 9.66
--------------------------------------------
Оценка
погрешности формулы Лагранжа определяют
из приближенного равенства
9.66
--------------------------------------------
Оценка
погрешности формулы Лагранжа определяют
из приближенного равенства
![]() --------------------------------------------
Высшей
степенью точности обладает
метод
Симпсона
--------------------------------------------
При
решении нелинейного уравнения за
неподвижный конец отрезка [a;b]
в
методе хорд выбирают конец отрезка, для
которого
--------------------------------------------
Высшей
степенью точности обладает
метод
Симпсона
--------------------------------------------
При
решении нелинейного уравнения за
неподвижный конец отрезка [a;b]
в
методе хорд выбирают конец отрезка, для
которого
![]() --------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=0.45
равно
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=0.45
равно
![]()
![]() 0.575
--------------------------------------------
Неподвижной
точкой (начальное приближение) при
решении уравнения
0.575
--------------------------------------------
Неподвижной
точкой (начальное приближение) при
решении уравнения
![]() методом
хорд
методом
хорд
![]() является
0
--------------------------------------------
Метод,
в котором подынтегральная функция
заменяется полиномом наименьшей степени,
называется
методом
прямоугольников
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
является
0
--------------------------------------------
Метод,
в котором подынтегральная функция
заменяется полиномом наименьшей степени,
называется
методом
прямоугольников
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения![]()
![]() методом
хорд служит
методом
хорд служит
![]() --------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
![]() для
функции, заданной таблично,
значение
функции в точке х=2.5
равно
для
функции, заданной таблично,
значение
функции в точке х=2.5
равно
![]()
![]() 9.8
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=1.36
равно
9.8
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=1.36
равно
![]()
![]() 4.66
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
4.66
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
![]()
![]() методом
половинного деления служит
методом
половинного деления служит
![]() --------------------------------------------
Изменение
степени интерполяционного полинома на
единицу (добавление в таблицу значений
функции одного узла)
ведет к полному
пересчету
формулы
Лагранжа
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
--------------------------------------------
Изменение
степени интерполяционного полинома на
единицу (добавление в таблицу значений
функции одного узла)
ведет к полному
пересчету
формулы
Лагранжа
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
![]()
![]() методом
половинного деления служит
методом
половинного деления служит
![]() --------------------------------------------
--------------------------------------------
![]() -
это
формула
Лагранжа
--------------------------------------------
Замена
некоторой функции y=f(x) другой функцией
g(x,a0,a1,…,a
n) таким образом, чтобы
отклонение g(x,a0,a1,…,an)
от f(x)
удовлетворяло в некоторой
области определенному условию называется
аппроксимацией
--------------------------------------------
Правилом
выбора итерирующей функции при решении
нелинейного уравнения методом итераций
является
-
это
формула
Лагранжа
--------------------------------------------
Замена
некоторой функции y=f(x) другой функцией
g(x,a0,a1,…,a
n) таким образом, чтобы
отклонение g(x,a0,a1,…,an)
от f(x)
удовлетворяло в некоторой
области определенному условию называется
аппроксимацией
--------------------------------------------
Правилом
выбора итерирующей функции при решении
нелинейного уравнения методом итераций
является
![]() --------------------------------------------
Корень
нелинейного уравнения f(x)=0 это
значение переменной х, обращающее
уравнение в
тождество
--------------------------------------------
Погрешность,
при вычислении определенного интеграла
--------------------------------------------
Корень
нелинейного уравнения f(x)=0 это
значение переменной х, обращающее
уравнение в
тождество
--------------------------------------------
Погрешность,
при вычислении определенного интеграла
 по
формуле трапеций
с шагом h=2, составляет
5.333
--------------------------------------------
Дана
подынтегральная функция f(x)=x2.
Численный метод, позволяющий вычислить
интеграл без ошибки, называется
методом
Симпсона
--------------------------------------------
Погрешность,при
вычислении определенного интеграла
по
формуле трапеций
с шагом h=2, составляет
5.333
--------------------------------------------
Дана
подынтегральная функция f(x)=x2.
Численный метод, позволяющий вычислить
интеграл без ошибки, называется
методом
Симпсона
--------------------------------------------
Погрешность,при
вычислении определенного интеграла
 по
формуле левых прямоугольников
с шагом
h=1, составляет
1
--------------------------------------------
Метод
Ньютона применять при решении нелинейного
уравнения не рекомендуется, если
по
формуле левых прямоугольников
с шагом
h=1, составляет
1
--------------------------------------------
Метод
Ньютона применять при решении нелинейного
уравнения не рекомендуется, если
![]() -
пологая
--------------------------------------------
Начальное
приближение к корню при решении
нелинейного уравнения это
значениe
х, обеспечивающее сходимость метода
уточнения
корня
--------------------------------------------
Оценка
погрешности значения интеграла
-
пологая
--------------------------------------------
Начальное
приближение к корню при решении
нелинейного уравнения это
значениe
х, обеспечивающее сходимость метода
уточнения
корня
--------------------------------------------
Оценка
погрешности значения интеграла
 ,
вычисленного по методу Симпсона с h=2 и
h=1,
по правилу Рунге составляет
0.019
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=3,6
равно
,
вычисленного по методу Симпсона с h=2 и
h=1,
по правилу Рунге составляет
0.019
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=3,6
равно
![]()
![]() 8.5
--------------------------------------------
Метод
численного интегрирования, в котором
подынтегральная функция заменяется
квадратичным полиномом,
называется
методом
Симпсона
--------------------------------------------
Метод,
не предназначенный для решения нелинейных
уравнений это
метод
прямоугольников
--------------------------------------------
Оценка
погрешности значения интеграла
8.5
--------------------------------------------
Метод
численного интегрирования, в котором
подынтегральная функция заменяется
квадратичным полиномом,
называется
методом
Симпсона
--------------------------------------------
Метод,
не предназначенный для решения нелинейных
уравнений это
метод
прямоугольников
--------------------------------------------
Оценка
погрешности значения интеграла
 ,
вычисленного по методу средних
прямоугольников
с h=2 и h=1,по правилу
Рунге составляет
0.333
--------------------------------------------
Неподвижной
точкой при решении уравнения
,
вычисленного по методу средних
прямоугольников
с h=2 и h=1,по правилу
Рунге составляет
0.333
--------------------------------------------
Неподвижной
точкой при решении уравнения
![]() методом
хорд
методом
хорд
![]() является
0
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P2(x) для функции,
заданной таблично,
значение функции
в точке х=0.18
равно
является
0
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P2(x) для функции,
заданной таблично,
значение функции
в точке х=0.18
равно
![]()
![]() 0.66
--------------------------------------------
Интерполяционный
полином наименьшей степени, это полином
степени
0
--------------------------------------------
Формула
0.66
--------------------------------------------
Интерполяционный
полином наименьшей степени, это полином
степени
0
--------------------------------------------
Формула
![]() предназначена
для вычисления элементарного интеграла
по формуле
Симпсона
--------------------------------------------
При
вычислении элементарного интеграла по
методу трапеции точки соединяются
прямой
--------------------------------------------
Существует
метод интегрирования
прямоугольников
--------------------------------------------
Погрешность,
при вычислении определенного интеграла
предназначена
для вычисления элементарного интеграла
по формуле
Симпсона
--------------------------------------------
При
вычислении элементарного интеграла по
методу трапеции точки соединяются
прямой
--------------------------------------------
Существует
метод интегрирования
прямоугольников
--------------------------------------------
Погрешность,
при вычислении определенного интеграла
 по
формуле Симпсона
с шагом h=3, составляет
0.051
--------------------------------------------
При
использовании формулы Лагранжа
располагать узлы интерполяции можно
в произвольном
порядке
--------------------------------------------
Шаг
равномерной сетки изменения x на отрезке
вычисляется по формуле (n-число
узлов) равен
h=(b-a)/(n-1)
--------------------------------------------
Неподвижной
точкой при решении нелинейного уравнения
по
формуле Симпсона
с шагом h=3, составляет
0.051
--------------------------------------------
При
использовании формулы Лагранжа
располагать узлы интерполяции можно
в произвольном
порядке
--------------------------------------------
Шаг
равномерной сетки изменения x на отрезке
вычисляется по формуле (n-число
узлов) равен
h=(b-a)/(n-1)
--------------------------------------------
Неподвижной
точкой при решении нелинейного уравнения
![]() методом
хорд
методом
хорд
![]() является
x=-1
--------------------------------------------
На
этапе уточнения корней нелинейного
уравнения определяют
значение корня
с заданной степенью
точности
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу Симпсона с h=2 и
h=1,если подынтегральная функции
задана
следующей таблицей, по правилу Рунге
составляет
является
x=-1
--------------------------------------------
На
этапе уточнения корней нелинейного
уравнения определяют
значение корня
с заданной степенью
точности
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу Симпсона с h=2 и
h=1,если подынтегральная функции
задана
следующей таблицей, по правилу Рунге
составляет
![]() 0.011
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу трапеций с h=0.2
и h=0.1, если функция задана таблично,
по
правилу Рунге
составляет
0.011
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу трапеций с h=0.2
и h=0.1, если функция задана таблично,
по
правилу Рунге
составляет
![]() 0.025
--------------------------------------------
Неподвижной
точкой при решении нелинейного уравнения
0.025
--------------------------------------------
Неподвижной
точкой при решении нелинейного уравнения
![]()
![]() методом
хорд служит
x=-1
--------------------------------------------
Шаг
интегрирования - это
расстояние между
значениями xi и
xi+1
--------------------------------------------
В
формуле правила Рунге
методом
хорд служит
x=-1
--------------------------------------------
Шаг
интегрирования - это
расстояние между
значениями xi и
xi+1
--------------------------------------------
В
формуле правила Рунге
![]() значение
коэффициента k в методах Симпсона,
левых и правых прямоугольников и
трапеций, равны соответственно
4, 1,
2
--------------------------------------------
По
величине конечных разностей сделать
вывод о степени интерполяционного
полинома
можно
--------------------------------------------
Задача
численного интегрирования требует
выполнения интерполяции при
вычислении
элементарного
интеграла
--------------------------------------------
Метод
правых прямоугольников имеет порядок
точности, равный
1
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=0.21
равно
значение
коэффициента k в методах Симпсона,
левых и правых прямоугольников и
трапеций, равны соответственно
4, 1,
2
--------------------------------------------
По
величине конечных разностей сделать
вывод о степени интерполяционного
полинома
можно
--------------------------------------------
Задача
численного интегрирования требует
выполнения интерполяции при
вычислении
элементарного
интеграла
--------------------------------------------
Метод
правых прямоугольников имеет порядок
точности, равный
1
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=0.21
равно
![]()
![]() 0.41
--------------------------------------------
Шаг
равномерной сетки изменения х на
отрезке [a;b]
вычисляется по формуле
(n – число узлов)
0.41
--------------------------------------------
Шаг
равномерной сетки изменения х на
отрезке [a;b]
вычисляется по формуле
(n – число узлов)
![]() --------------------------------------------
Обеспечить
вычисление интеграла с заданной точностью
можно, используя
метод двойного
просчета
--------------------------------------------
Метод
решения нелинейного уравнения сходится,
если
за конечное число итераций корень
найден с заданной
точностью
--------------------------------------------
Вторая
интерполяционная формула Ньютона
используется, когда точка интерполяции
находится
в конце таблицы с
равноотстоящими
узлами
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
--------------------------------------------
Обеспечить
вычисление интеграла с заданной точностью
можно, используя
метод двойного
просчета
--------------------------------------------
Метод
решения нелинейного уравнения сходится,
если
за конечное число итераций корень
найден с заданной
точностью
--------------------------------------------
Вторая
интерполяционная формула Ньютона
используется, когда точка интерполяции
находится
в конце таблицы с
равноотстоящими
узлами
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
![]()
![]() методом
простой итерации служит
любое значение
методом
простой итерации служит
любое значение
![]() --------------------------------------------
Интерполяционных
полиномов степени n существует
один
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=3,25
равно
--------------------------------------------
Интерполяционных
полиномов степени n существует
один
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=3,25
равно
![]()
![]() 6.0
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу Симпсона с h=2 и
h=1, если подынтегральная функция
задана
следующей таблицей, по правилу Рунге
составляет
6.0
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу Симпсона с h=2 и
h=1, если подынтегральная функция
задана
следующей таблицей, по правилу Рунге
составляет
![]() 0.047
--------------------------------------------
Метод
численного интегрирования, в котором
подынтегральная функция заменяется
полиномом нулевой степени,
называется
методом
прямоугольников
--------------------------------------------
Оценка
погрешности значения интеграла
0.047
--------------------------------------------
Метод
численного интегрирования, в котором
подынтегральная функция заменяется
полиномом нулевой степени,
называется
методом
прямоугольников
--------------------------------------------
Оценка
погрешности значения интеграла
 ,
вычисленного по методу левых прямоугольников
с h=2 и h=1, по правилу Рунге составляет
5
--------------------------------------------
При
решении нелинейного уравнения малая
скорость сходимости характерна для
метода
половинного
деления
--------------------------------------------
Термин,
который относится к методам решения
нелинейных уравнений это
итерация
--------------------------------------------
Нелинейное
уравнение это
алгебраическое или
трансцендентное
уравнение
--------------------------------------------
Для
подынтегральной функции
,
вычисленного по методу левых прямоугольников
с h=2 и h=1, по правилу Рунге составляет
5
--------------------------------------------
При
решении нелинейного уравнения малая
скорость сходимости характерна для
метода
половинного
деления
--------------------------------------------
Термин,
который относится к методам решения
нелинейных уравнений это
итерация
--------------------------------------------
Нелинейное
уравнение это
алгебраическое или
трансцендентное
уравнение
--------------------------------------------
Для
подынтегральной функции
![]() наиболее
точный результат будет, если применить
метод
Симпсона
--------------------------------------------
При
увеличении степени интерполяционного
полинома на единицу формула Ньютона
имеет следующее преимущество перед
формулой Лагранжа
не нужно пересчитывать
коэффициенты
--------------------------------------------
Универсальность
формулы Лагранжа заключается в возможности
все ответы
верные
--------------------------------------------
Сплайн
- это
Функция которая на каждом
частичном отрезке интерполяции является
алгебраическим многочленом,
а на всем
заданном отрезке непрерывна вместе с
несколькими своими
производными.
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
наиболее
точный результат будет, если применить
метод
Симпсона
--------------------------------------------
При
увеличении степени интерполяционного
полинома на единицу формула Ньютона
имеет следующее преимущество перед
формулой Лагранжа
не нужно пересчитывать
коэффициенты
--------------------------------------------
Универсальность
формулы Лагранжа заключается в возможности
все ответы
верные
--------------------------------------------
Сплайн
- это
Функция которая на каждом
частичном отрезке интерполяции является
алгебраическим многочленом,
а на всем
заданном отрезке непрерывна вместе с
несколькими своими
производными.
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
![]()
![]() методом
Ньютона служит
методом
Ньютона служит
![]() --------------------------------------------
Необходимым
условием существования корня нелинейного
уравнения на отрезке [a;b] является
--------------------------------------------
Необходимым
условием существования корня нелинейного
уравнения на отрезке [a;b] является
![]() --------------------------------------------
Оценка
погрешности значения интеграла
--------------------------------------------
Оценка
погрешности значения интеграла
 ,
вычисленного по методу трапеций с h=2 и
h=1,
по правилу Рунге составляет
0.667
--------------------------------------------
Метод
трапеций имеет порядок точности, равный
2
--------------------------------------------
Формула
для вычисления определенного интеграла
по методу левых прямоугольников имеет
вид
,
вычисленного по методу трапеций с h=2 и
h=1,
по правилу Рунге составляет
0.667
--------------------------------------------
Метод
трапеций имеет порядок точности, равный
2
--------------------------------------------
Формула
для вычисления определенного интеграла
по методу левых прямоугольников имеет
вид
![]() --------------------------------------------
Уменьшение
шага интегрирования ,приводит к
уменьшению
погрешности
--------------------------------------------
Термин
- «метод расходится» означает
очередное
приближение отдаляется от корня
уравнения
--------------------------------------------
Первым
приближением к корню, отделенному на
отрезке [a;b],
при решении нелинейного
уравнения методом половинного деления
служит
--------------------------------------------
Уменьшение
шага интегрирования ,приводит к
уменьшению
погрешности
--------------------------------------------
Термин
- «метод расходится» означает
очередное
приближение отдаляется от корня
уравнения
--------------------------------------------
Первым
приближением к корню, отделенному на
отрезке [a;b],
при решении нелинейного
уравнения методом половинного деления
служит
![]() --------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
![]() для
функции, заданной таблично,
значение
функции в точке х=6.9
равно
для
функции, заданной таблично,
значение
функции в точке х=6.9
равно
![]()
![]() 7.5
--------------------------------------------
Формула
(b-a)/n служит для определения (n –
число разбиений)
шага
интегрирования
--------------------------------------------
График
функции на отрезке [a;b] пересекает
ось ОХ только один раз, если выполняется
условие
7.5
--------------------------------------------
Формула
(b-a)/n служит для определения (n –
число разбиений)
шага
интегрирования
--------------------------------------------
График
функции на отрезке [a;b] пересекает
ось ОХ только один раз, если выполняется
условие
![]() --------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
![]() для
функции, заданной таблично,
значение
функции в точке х=2,5
равно
для
функции, заданной таблично,
значение
функции в точке х=2,5
равно

![]() 2.05
--------------------------------------------
Погрешность,
при вычислении определенного интеграла
2.05
--------------------------------------------
Погрешность,
при вычислении определенного интеграла
 по
формуле средних прямоугольников
с
шагом h=3, составляет
4.5
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=0.15
равно
по
формуле средних прямоугольников
с
шагом h=3, составляет
4.5
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=0.15
равно
![]()
![]() -0.65
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
-0.65
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения![]()
![]() методом
половинного деления служит
методом
половинного деления служит
![]() --------------------------------------------
Формула
погрешности
--------------------------------------------
Формула
погрешности
![]() ,
где
,
где
![]() применятся
в
методе
трапеций
--------------------------------------------
Начальным
приближением к корню при решении
налинейного уравнения
применятся
в
методе
трапеций
--------------------------------------------
Начальным
приближением к корню при решении
налинейного уравнения
![]()
![]() методом
простой итерации служит
любое
значение
методом
простой итерации служит
любое
значение![]() --------------------------------------------
Шаг
интерполяции это
расстояние между
узлами
интерполяции
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу Симпсона с h=2 и
h=1, если функция задана таблично,
по
правилу Рунге
составляет
--------------------------------------------
Шаг
интерполяции это
расстояние между
узлами
интерполяции
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу Симпсона с h=2 и
h=1, если функция задана таблично,
по
правилу Рунге
составляет
![]() 0.122
--------------------------------------------
Конечные
разности используются в
интерполяцилнных
формулах
Ньютона
--------------------------------------------
Погрешность
интегрирования при уменьшении числа
разбиений
увеличится
--------------------------------------------
При
отделении корней нелинейных уравнений
критическими точками считаются
0.122
--------------------------------------------
Конечные
разности используются в
интерполяцилнных
формулах
Ньютона
--------------------------------------------
Погрешность
интегрирования при уменьшении числа
разбиений
увеличится
--------------------------------------------
При
отделении корней нелинейных уравнений
критическими точками считаются
![]() --------------------------------------------
Дана
подынтегральная функция y=5x3
Метод численного интегрирования,
который дает наиболее точный результат
метод
Симпсона
--------------------------------------------
Если
при построении интерполяционных
полиномов по формулам Лагранжа и Ньютона
были использованы одни и те же узлы,
то
результаты могут отличаться только
погрешностью
вычислений
--------------------------------------------
Оценка
погрешности значения интеграла
--------------------------------------------
Дана
подынтегральная функция y=5x3
Метод численного интегрирования,
который дает наиболее точный результат
метод
Симпсона
--------------------------------------------
Если
при построении интерполяционных
полиномов по формулам Лагранжа и Ньютона
были использованы одни и те же узлы,
то
результаты могут отличаться только
погрешностью
вычислений
--------------------------------------------
Оценка
погрешности значения интеграла
![]() ,
вычисленного по методу средних
прямоугольников
с h=2 и h=1, по правилу
Рунге составляет
11.221
--------------------------------------------
Этап
отделения корней при решении нелинейного
уравнения необходим, потому что
уравнение
может иметь несколько
корней
--------------------------------------------
В
методе двойного просчета коэффициент
k в формуле
,
вычисленного по методу средних
прямоугольников
с h=2 и h=1, по правилу
Рунге составляет
11.221
--------------------------------------------
Этап
отделения корней при решении нелинейного
уравнения необходим, потому что
уравнение
может иметь несколько
корней
--------------------------------------------
В
методе двойного просчета коэффициент
k в формуле
![]() означает
порядок точности
метода
--------------------------------------------
Многочлены
Лагранжа и Ньютона предназначены для
получения приближенной аналитической
записи
функции
--------------------------------------------
Основное
условие интерполяции это
полное
совпадение значений интерполируемой
и интерполирующих функций во всех узлах
интерполяции
--------------------------------------------
Единственность
решения задачи полиномиального
интерполирования обеспечивается
выполнением условий интерполирования
в n+1 точке из интервала приближения
(n – порядок
полинома)
--------------------------------------------
Вычисление
интеграла с заданной точностью можно
обеспечить, используя
метод двойного
просчета
--------------------------------------------
Метод
Симпсона имеет порядок точности, равный
4
--------------------------------------------
Процесс
решения нелинейного уравнения состоит
из
двух
этапов
--------------------------------------------
Добавление
очередного узла интерполяции при
использовании формул Ньютона требует
вычисления дополнительного
слагаемого
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=1.4
равно
означает
порядок точности
метода
--------------------------------------------
Многочлены
Лагранжа и Ньютона предназначены для
получения приближенной аналитической
записи
функции
--------------------------------------------
Основное
условие интерполяции это
полное
совпадение значений интерполируемой
и интерполирующих функций во всех узлах
интерполяции
--------------------------------------------
Единственность
решения задачи полиномиального
интерполирования обеспечивается
выполнением условий интерполирования
в n+1 точке из интервала приближения
(n – порядок
полинома)
--------------------------------------------
Вычисление
интеграла с заданной точностью можно
обеспечить, используя
метод двойного
просчета
--------------------------------------------
Метод
Симпсона имеет порядок точности, равный
4
--------------------------------------------
Процесс
решения нелинейного уравнения состоит
из
двух
этапов
--------------------------------------------
Добавление
очередного узла интерполяции при
использовании формул Ньютона требует
вычисления дополнительного
слагаемого
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=1.4
равно
![]()
![]() 3.4
--------------------------------------------
Приведение
нелинейного уравнения
3.4
--------------------------------------------
Приведение
нелинейного уравнения
![]() к
виду, удобному для итераций, означает
замена
к
виду, удобному для итераций, означает
замена
![]() равносильным
равносильным
![]() --------------------------------------------
При
использовании интерполяционных формул
Ньютона располагать узлы в произвольном
порядке
нельзя
--------------------------------------------
Формула
для вычисления определенного интеграла
по методу правых прямоугольников имеет
вид
--------------------------------------------
При
использовании интерполяционных формул
Ньютона располагать узлы в произвольном
порядке
нельзя
--------------------------------------------
Формула
для вычисления определенного интеграла
по методу правых прямоугольников имеет
вид
![]() --------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=0,11
равно
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=0,11
равно
![]()
![]() 0.77
--------------------------------------------
Для
построения второй интерполирующей
формулы Ньютона используется многочлен
вида
0.77
--------------------------------------------
Для
построения второй интерполирующей
формулы Ньютона используется многочлен
вида
![]() --------------------------------------------
Неподвижной
точкой при решении нелинейного уравнения
--------------------------------------------
Неподвижной
точкой при решении нелинейного уравнения
![]() ,
если корень отделен на отрезке
,
если корень отделен на отрезке
![]() методом
хорд, служит
x=3
--------------------------------------------
Методом
интегрирования с наименьшей степенью
точности является
метод
прямоугольников
--------------------------------------------
Оценка
погрешности значения интеграла
методом
хорд, служит
x=3
--------------------------------------------
Методом
интегрирования с наименьшей степенью
точности является
метод
прямоугольников
--------------------------------------------
Оценка
погрешности значения интеграла
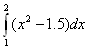 ,
вычисленного по методу средних
прямоугольников
с h=1 и h=0.5,по правилу
Рунге составляет
0.021
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
,
вычисленного по методу средних
прямоугольников
с h=1 и h=0.5,по правилу
Рунге составляет
0.021
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
![]()
![]() методом
хорд служит
методом
хорд служит
![]() --------------------------------------------
К
методам отделения корня нелинейного
уравнения не относится
метод
итераций
--------------------------------------------
Меньшее
количество интервалов разбиения при
вычислении интеграла с заданной точностью
потребуется для
метода
Симпсона
--------------------------------------------
Метод
двойного просчета служит для
вычисления
интеграла с заданной
точностью
--------------------------------------------
Шаг
интегрирования (h), в формуле прямоугольников
равен
h=xi+1-xi
--------------------------------------------
Если
при решении нелинейного уравнения на
заданном отрезке имеется два корня, то
о методе итераций можно сказать
сходимость метода не
гарантирована
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=2.75
равно
--------------------------------------------
К
методам отделения корня нелинейного
уравнения не относится
метод
итераций
--------------------------------------------
Меньшее
количество интервалов разбиения при
вычислении интеграла с заданной точностью
потребуется для
метода
Симпсона
--------------------------------------------
Метод
двойного просчета служит для
вычисления
интеграла с заданной
точностью
--------------------------------------------
Шаг
интегрирования (h), в формуле прямоугольников
равен
h=xi+1-xi
--------------------------------------------
Если
при решении нелинейного уравнения на
заданном отрезке имеется два корня, то
о методе итераций можно сказать
сходимость метода не
гарантирована
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=2.75
равно
![]()
![]() 6.875
--------------------------------------------
Правилом
выбора неподвижной точки при решении
нелинейного уравнения методом хорд
является
6.875
--------------------------------------------
Правилом
выбора неподвижной точки при решении
нелинейного уравнения методом хорд
является
![]() --------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения![]()
![]() методом
половинного деления служит
методом
половинного деления служит
![]() --------------------------------------------
Формула
погрешности
--------------------------------------------
Формула
погрешности
![]() ,
где
,
где
![]() применятся
в
методе
Симпсона
--------------------------------------------
Узлы
интерполяции это
значения xi
(i =
0,1,2,…,n)
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
применятся
в
методе
Симпсона
--------------------------------------------
Узлы
интерполяции это
значения xi
(i =
0,1,2,…,n)
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
![]()
![]() методом
Ньютона служит
методом
Ньютона служит
![]() --------------------------------------------
При
использовании формулы Лагранжа добавление
дополнительного узла
потребует
полного пересчета
коэффициентов
--------------------------------------------
На
этапе отделения корней нелинейного
уравнения используется
графический
метод
--------------------------------------------
Неподвижной
точкой при решении нелинейного уравнения
--------------------------------------------
При
использовании формулы Лагранжа добавление
дополнительного узла
потребует
полного пересчета
коэффициентов
--------------------------------------------
На
этапе отделения корней нелинейного
уравнения используется
графический
метод
--------------------------------------------
Неподвижной
точкой при решении нелинейного уравнения
![]()
![]() методом
хорд служит
x=0.5
--------------------------------------------
В
формуле Рунге
методом
хорд служит
x=0.5
--------------------------------------------
В
формуле Рунге
 коэффициент
k для формул трапеций и средних
прямоугольников равен
2
--------------------------------------------
Понятия
«интерполяция» и «экстраполяция» это
«интерполяция» - поиск значений
функции для точек внутри таблицы, а
«экстраполяция» - вне
таблицы
--------------------------------------------
Формула
Симпсона имеет следующий вид
коэффициент
k для формул трапеций и средних
прямоугольников равен
2
--------------------------------------------
Понятия
«интерполяция» и «экстраполяция» это
«интерполяция» - поиск значений
функции для точек внутри таблицы, а
«экстраполяция» - вне
таблицы
--------------------------------------------
Формула
Симпсона имеет следующий вид
![]() --------------------------------------------
2-ю
интерполяционную формулу Ньютона
целесообразно применять, если
искомая
точка расположена ближе к концу
таблицы
--------------------------------------------
Оценка
погрешностей численного интегрирования
по формуле левых прямоугольников
--------------------------------------------
2-ю
интерполяционную формулу Ньютона
целесообразно применять, если
искомая
точка расположена ближе к концу
таблицы
--------------------------------------------
Оценка
погрешностей численного интегрирования
по формуле левых прямоугольников
![]() ,
,
![]() --------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
![]()
![]() методом
Ньютона служит
методом
Ньютона служит
![]() --------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
![]()
![]() методом
хорд служит
методом
хорд служит
![]() --------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
![]() для
функции, заданной таблично,
значение
функции в точке х=0.2
равно
для
функции, заданной таблично,
значение
функции в точке х=0.2
равно
![]()
![]() 4.375
--------------------------------------------
1-ю
интерполяционную формулу Ньютона
целесообразно применять, если
искомая
точка расположена ближе к началу
таблицы
--------------------------------------------
Оценка
погрешности значения интеграла
4.375
--------------------------------------------
1-ю
интерполяционную формулу Ньютона
целесообразно применять, если
искомая
точка расположена ближе к началу
таблицы
--------------------------------------------
Оценка
погрешности значения интеграла
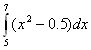 ,
вычисленного по методу средних
прямоугольников
с h=1 и h=0.5, по правилу
Рунге составляет
0.042
--------------------------------------------
Порядок
конечной разности наивысшего порядка,
полученный по n исходным точкам
функции равен
n-1
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=1.8
равно
,
вычисленного по методу средних
прямоугольников
с h=1 и h=0.5, по правилу
Рунге составляет
0.042
--------------------------------------------
Порядок
конечной разности наивысшего порядка,
полученный по n исходным точкам
функции равен
n-1
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=1.8
равно
![]()
![]() 4,6
--------------------------------------------
Нахождение
возможно более узкого отрезка, содержащего
только один корень уравнения, называется
отделением
корней
--------------------------------------------
Метод
половинного деления всегда находит
корень нелинейного уравнения f(x)=0,
если
выполнено условие существования
и единственности корня на
отрезке
--------------------------------------------
Начальным
приближением к корню при решении
налинейного уравнения
4,6
--------------------------------------------
Нахождение
возможно более узкого отрезка, содержащего
только один корень уравнения, называется
отделением
корней
--------------------------------------------
Метод
половинного деления всегда находит
корень нелинейного уравнения f(x)=0,
если
выполнено условие существования
и единственности корня на
отрезке
--------------------------------------------
Начальным
приближением к корню при решении
налинейного уравнения
![]()
![]() методом
половинного деления служит
методом
половинного деления служит
![]() --------------------------------------------
Формула
для вычисления определенного интеграла
по методу средних прямоугольников имеет
вид
--------------------------------------------
Формула
для вычисления определенного интеграла
по методу средних прямоугольников имеет
вид
![]() --------------------------------------------
Формулу
Ньютона можно применять для
таблиц
с равноотстоящими
узлами
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
--------------------------------------------
Формулу
Ньютона можно применять для
таблиц
с равноотстоящими
узлами
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
![]() для
функции, заданной таблично,
значение
функции в точке х=2,6
равно
для
функции, заданной таблично,
значение
функции в точке х=2,6
равно
![]()
![]() 15.6
--------------------------------------------
Погрешность,при
вычислении определенного интеграла
15.6
--------------------------------------------
Погрешность,при
вычислении определенного интеграла
 по
формуле трапеций с шагом h=1, составляет
0.667
--------------------------------------------
Дана
подынтегральная функция y=5x.
Численный
метод, с интерполяционным многочленом
наименьшей степени, позволяющий вычислить
интеграл с наименьшей погрешностью
называется
метод
трапеций
--------------------------------------------
Единственность
решения полиномиального интерполирования
обеспечивается
выполнением условия
интерполирования во всех узлах
интерполяции
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
по
формуле трапеций с шагом h=1, составляет
0.667
--------------------------------------------
Дана
подынтегральная функция y=5x.
Численный
метод, с интерполяционным многочленом
наименьшей степени, позволяющий вычислить
интеграл с наименьшей погрешностью
называется
метод
трапеций
--------------------------------------------
Единственность
решения полиномиального интерполирования
обеспечивается
выполнением условия
интерполирования во всех узлах
интерполяции
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
![]() для
функции, заданной таблично,
значение
функции в точке х=0.25
равно
для
функции, заданной таблично,
значение
функции в точке х=0.25
равно
![]()
![]() 4.75
--------------------------------------------
В
методе Симпсона количество интервалов
разбиения должно быть
кратным
двум
--------------------------------------------
Формула
трапеций точно вычисляет интеграл, если
подынтегральная функция
линейная
--------------------------------------------
Кубатурой
называется
вычисление интеграла 2-х
переменных
--------------------------------------------
В
качестве аппроксимирующей функции чаще
всего используют алгебраический
многочлен вида
4.75
--------------------------------------------
В
методе Симпсона количество интервалов
разбиения должно быть
кратным
двум
--------------------------------------------
Формула
трапеций точно вычисляет интеграл, если
подынтегральная функция
линейная
--------------------------------------------
Кубатурой
называется
вычисление интеграла 2-х
переменных
--------------------------------------------
В
качестве аппроксимирующей функции чаще
всего используют алгебраический
многочлен вида
![]() --------------------------------------------
Используя
одни и те же узлы интерполяции, построить
несколько интерполяционных полиномов
нельзя
--------------------------------------------
При
решении задачи численного интегрирования
интерполяция используется
на этапе
вычисления элементарного
интеграла
--------------------------------------------
Метод
интегрирования, который наилучшим
образом подходит для вычисления интеграла
линейной функции,
называется
методом
трапеций
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу левых прямоугольников
с h=0.2 и h=0.1, если подынтегральная функция
задана следующей таблицей, по правилу
Рунге
составляет
--------------------------------------------
Используя
одни и те же узлы интерполяции, построить
несколько интерполяционных полиномов
нельзя
--------------------------------------------
При
решении задачи численного интегрирования
интерполяция используется
на этапе
вычисления элементарного
интеграла
--------------------------------------------
Метод
интегрирования, который наилучшим
образом подходит для вычисления интеграла
линейной функции,
называется
методом
трапеций
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу левых прямоугольников
с h=0.2 и h=0.1, если подынтегральная функция
задана следующей таблицей, по правилу
Рунге
составляет
![]() 0.129
--------------------------------------------
Метод
решения нелинейного уравнения, обладающий
квадратичной сходимостью это
метод
Ньютона
--------------------------------------------
Если
интерполируемая функция f(x) задана
в (n+1) равноотстоящих узлах,
то для
ее интерполяции удобнее использовать
формулы
Ньютона
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу левых прямоугольников
с h=0.2 и h=0.1, если функция задана таблично,
по правилу Рунге
составляет
0.129
--------------------------------------------
Метод
решения нелинейного уравнения, обладающий
квадратичной сходимостью это
метод
Ньютона
--------------------------------------------
Если
интерполируемая функция f(x) задана
в (n+1) равноотстоящих узлах,
то для
ее интерполяции удобнее использовать
формулы
Ньютона
--------------------------------------------
Оценка
погрешности значения интеграла,
вычисленного по методу левых прямоугольников
с h=0.2 и h=0.1, если функция задана таблично,
по правилу Рунге
составляет
![]() 0.033
--------------------------------------------
Вставьте
пропущенные коэффициенты в формуле
Симпсона (в соответствующем порядке)
0.033
--------------------------------------------
Вставьте
пропущенные коэффициенты в формуле
Симпсона (в соответствующем порядке)
 4,
2
--------------------------------------------
Замена
таблично заданной функции y=f(x) другой
функцией g(x), такой, что
4,
2
--------------------------------------------
Замена
таблично заданной функции y=f(x) другой
функцией g(x), такой, что
![]() g(xi)=fxi)
(i=0,1,2,…,n), это -
интерполяция
--------------------------------------------
Формула
g(xi)=fxi)
(i=0,1,2,…,n), это -
интерполяция
--------------------------------------------
Формула
![]() служит
для определения (n – число разбиений)
шага
интегрирования
--------------------------------------------
Метод
хорд применяется на этапе
уточнения
корня
--------------------------------------------
Оценка
погрешности значения интеграла
служит
для определения (n – число разбиений)
шага
интегрирования
--------------------------------------------
Метод
хорд применяется на этапе
уточнения
корня
--------------------------------------------
Оценка
погрешности значения интеграла
 ,
вычисленного по методу трапеций
с
h=4 и h=2, по правилу Рунге составляет
5.333
--------------------------------------------
Метод
прямоугольников позволяет получить
точное значение интеграла, если
подынтегральная функция – полином
0 –ой
степени
--------------------------------------------
Геометрической
интерпретацией задачи интерполяции
является построение
графиков
интерполируемой и интерполирующей
функций с совпадением значений в узлах
интерполяции
--------------------------------------------
Элементарный
отрезок интегрирования в методе Симпсона
равен
двум шагам
интегрирования
--------------------------------------------
Формулу
Лагранжа можно применять для
таблиц
как с различными расстояниями между
узлами, так и с равноотстоящими
узлами
--------------------------------------------
Зависимость
между числом узлов интерполяции и
степенью интерполяционного многочлена
состоит в том, что
степень интерполяционного
многочлена на единицу меньше числа
узлов
--------------------------------------------
При
вычислении элементарного интеграла по
методу прямоугольников точки соединяются
прямой
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
,
вычисленного по методу трапеций
с
h=4 и h=2, по правилу Рунге составляет
5.333
--------------------------------------------
Метод
прямоугольников позволяет получить
точное значение интеграла, если
подынтегральная функция – полином
0 –ой
степени
--------------------------------------------
Геометрической
интерпретацией задачи интерполяции
является построение
графиков
интерполируемой и интерполирующей
функций с совпадением значений в узлах
интерполяции
--------------------------------------------
Элементарный
отрезок интегрирования в методе Симпсона
равен
двум шагам
интегрирования
--------------------------------------------
Формулу
Лагранжа можно применять для
таблиц
как с различными расстояниями между
узлами, так и с равноотстоящими
узлами
--------------------------------------------
Зависимость
между числом узлов интерполяции и
степенью интерполяционного многочлена
состоит в том, что
степень интерполяционного
многочлена на единицу меньше числа
узлов
--------------------------------------------
При
вычислении элементарного интеграла по
методу прямоугольников точки соединяются
прямой
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
![]()
![]() методом
половинного деления служит
методом
половинного деления служит
![]() --------------------------------------------
Наивысшую
точность при одном и том же шаге
интегрирования позволяет обеспечить
метод
Симпсона
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=-0.75
равно
--------------------------------------------
Наивысшую
точность при одном и том же шаге
интегрирования позволяет обеспечить
метод
Симпсона
--------------------------------------------
При
построении линейного интерполяционного
многочлена Ньютона P1(x) для функции,
заданной таблично,
значение функции
в точке х=-0.75
равно
![]()
![]() 6.425
--------------------------------------------
Численное
значение интеграла функции одной
переменной называют
квадратурой
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
6.425
--------------------------------------------
Численное
значение интеграла функции одной
переменной называют
квадратурой
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
![]()
![]() методом
хорд служит
методом
хорд служит
![]() --------------------------------------------
Если
точка интерполяции Х находится в
начале таблицы с равноотстоящими узлами,
то для построения интерполяционного
полинома с возможно меньшей погрешностью
используется
первая формула
Ньютона
--------------------------------------------
Экстраполяция
- это
прогнозирование поведения
функции за пределами интервала заданных
точек
--------------------------------------------
Перенумерация
узлов при построении формулы Лагранжа
применяется для
уменьшения
погрешности
--------------------------------------------
Для
подынтегральной функции
--------------------------------------------
Если
точка интерполяции Х находится в
начале таблицы с равноотстоящими узлами,
то для построения интерполяционного
полинома с возможно меньшей погрешностью
используется
первая формула
Ньютона
--------------------------------------------
Экстраполяция
- это
прогнозирование поведения
функции за пределами интервала заданных
точек
--------------------------------------------
Перенумерация
узлов при построении формулы Лагранжа
применяется для
уменьшения
погрешности
--------------------------------------------
Для
подынтегральной функции
![]() наиболее
точный результат будет, если применить
метод
Симпсона
--------------------------------------------
Оценка
погрешности значения интеграла
наиболее
точный результат будет, если применить
метод
Симпсона
--------------------------------------------
Оценка
погрешности значения интеграла
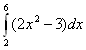 ,
вычисленного по методу трапеций с h=2 и
h=1,
если подынтегральная функция, по
правилу Рунге составляет
1.333
--------------------------------------------
Формула
трапеций это
,
вычисленного по методу трапеций с h=2 и
h=1,
если подынтегральная функция, по
правилу Рунге составляет
1.333
--------------------------------------------
Формула
трапеций это
![]() --------------------------------------------
Метод
левых прямоугольников имеет порядок
точности, равный
1
--------------------------------------------
Определённый
интеграл в методах численного
интегрирования вычисляется по формуле
--------------------------------------------
Метод
левых прямоугольников имеет порядок
точности, равный
1
--------------------------------------------
Определённый
интеграл в методах численного
интегрирования вычисляется по формуле
![]() --------------------------------------------
Дана
подынтегральная функция y=5.
Численный
метод, с интерполяционным многочленом
наименьшей степени, позволяющий вычислить
интеграл без ошибки, называется
метод
средних
прямоугольников
--------------------------------------------
Неподвижной
точкой при решении нелинейного уравнения
--------------------------------------------
Дана
подынтегральная функция y=5.
Численный
метод, с интерполяционным многочленом
наименьшей степени, позволяющий вычислить
интеграл без ошибки, называется
метод
средних
прямоугольников
--------------------------------------------
Неподвижной
точкой при решении нелинейного уравнения![]()
![]() методом
хорд служит
x=0
--------------------------------------------
Корень
методом
хорд служит
x=0
--------------------------------------------
Корень
![]() нелинейного
уравнения f(x)=0 считается отделенным
на отрезке [a;b],
в котором содержится
1 корень
--------------------------------------------
За
начальное приближение при решении
нелинейного уравнения методом итераций
принимают
нелинейного
уравнения f(x)=0 считается отделенным
на отрезке [a;b],
в котором содержится
1 корень
--------------------------------------------
За
начальное приближение при решении
нелинейного уравнения методом итераций
принимают
![]() ,
если
,
если
![]() --------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
![]() для
функции, заданной таблично,
значение
функции в точке х=2,65
равно
для
функции, заданной таблично,
значение
функции в точке х=2,65
равно
![]()
![]() 6.13
--------------------------------------------
Если
подынтегральная функция задана таблично,
то применение метода средних прямоугольников
не всегда
возможно
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
6.13
--------------------------------------------
Если
подынтегральная функция задана таблично,
то применение метода средних прямоугольников
не всегда
возможно
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
![]() для
функции, заданной таблично,
значение
функции в точке х=2,2
равно
для
функции, заданной таблично,
значение
функции в точке х=2,2
равно
![]()
![]() 14.4
--------------------------------------------
В
точке корня функция равна
нулю
--------------------------------------------
Погрешность
значения интеграла, вычисленного по
методу правых прямоугольников с h=0.2 и
h=0.1, если подынтегральная функция
задана
таблицей, по правилу Рунге
составляет
14.4
--------------------------------------------
В
точке корня функция равна
нулю
--------------------------------------------
Погрешность
значения интеграла, вычисленного по
методу правых прямоугольников с h=0.2 и
h=0.1, если подынтегральная функция
задана
таблицей, по правилу Рунге
составляет
![]() 0.031
--------------------------------------------
Пара
методов, обеспечивающих точность одного
порядка это
метод трапеций и метод
средних
прямоугольников
--------------------------------------------
Степень
интерполяционного полинома Ньютона
при трех известных точках интерполируемой
функции может быть равна
0, 1
или 2
–ой
--------------------------------------------
Уточнить
корень нелинейного уравнения графическим
методом
нельзя
--------------------------------------------
В
методе Симпсона подынтегральная функция
заменяется интерполяционным многочленом
2-й
степени
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
0.031
--------------------------------------------
Пара
методов, обеспечивающих точность одного
порядка это
метод трапеций и метод
средних
прямоугольников
--------------------------------------------
Степень
интерполяционного полинома Ньютона
при трех известных точках интерполируемой
функции может быть равна
0, 1
или 2
–ой
--------------------------------------------
Уточнить
корень нелинейного уравнения графическим
методом
нельзя
--------------------------------------------
В
методе Симпсона подынтегральная функция
заменяется интерполяционным многочленом
2-й
степени
--------------------------------------------
Начальным
приближением к корню при решении
нелинейного уравнения
![]()
![]() методом
половинного деления служит
методом
половинного деления служит
![]() --------------------------------------------
Метод
средних прямоугольников имеет порядок
точности, равный
2
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
--------------------------------------------
Метод
средних прямоугольников имеет порядок
точности, равный
2
--------------------------------------------
При
построении линейного интерполяционного
многочлена Лагранжа
![]() для
функции, заданной таблично,
значение
функции в точке
х=0.18,равно
для
функции, заданной таблично,
значение
функции в точке
х=0.18,равно
![]()
![]() -0.58
--------------------------------------------
Оценка
погрешностей численного интегрирования
по формуле правых прямоугольников
-0.58
--------------------------------------------
Оценка
погрешностей численного интегрирования
по формуле правых прямоугольников
![]() ,
,
![]() --------------------------------------------
Интерполяция
вида
--------------------------------------------
Интерполяция
вида
![]() называется
квадратичной
--------------------------------------------
Формулой
трапеции является формула
называется
квадратичной
--------------------------------------------
Формулой
трапеции является формула
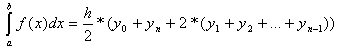 --------------------------------------------
В
формуле Рунге
--------------------------------------------
В
формуле Рунге
 коэффициент
k для формул левых и правых прямоугольников
равен
1
--------------------------------------------
Наименьшее
количество интервалов разбиения в
методе Симпсона равно
2
--------------------------------------------
Пара
методов, обеспечивающих точность одного
и того же порядка это
методы левых и
правых
прямоугольников
--------------------------------------------
Корень
x на отрезке [a;b] существует, если
f(x) на концах отрезка имеет разные
знаки
--------------------------------------------
Интерполирующая
функция это
функция, на которую
заменяют таблично заданную
функцию
--------------------------------------------
При
уменьшении количества узлов интерполяции
точность интерполяции
уменьшается
--------------------------------------------
При
использовании n+1 узла таблицы,
интерполяционный полином Лагранжа
является полиномом
n –ой
степени
--------------------------------------------
коэффициент
k для формул левых и правых прямоугольников
равен
1
--------------------------------------------
Наименьшее
количество интервалов разбиения в
методе Симпсона равно
2
--------------------------------------------
Пара
методов, обеспечивающих точность одного
и того же порядка это
методы левых и
правых
прямоугольников
--------------------------------------------
Корень
x на отрезке [a;b] существует, если
f(x) на концах отрезка имеет разные
знаки
--------------------------------------------
Интерполирующая
функция это
функция, на которую
заменяют таблично заданную
функцию
--------------------------------------------
При
уменьшении количества узлов интерполяции
точность интерполяции
уменьшается
--------------------------------------------
При
использовании n+1 узла таблицы,
интерполяционный полином Лагранжа
является полиномом
n –ой
степени
--------------------------------------------
Тестовые задания по теме «Методы решения обыкновенных дифференциальных уравнений» Тесты 1-го блока сложности
-
Обыкновенное дифференциальное уравнение это...
-
дифференциальное уравнение от одной переменной*
-
дифференциальное уравнение первого порядка
-
дифференциальное уравнение n-ого порядка
-
в списке нет правильного ответа
-
-
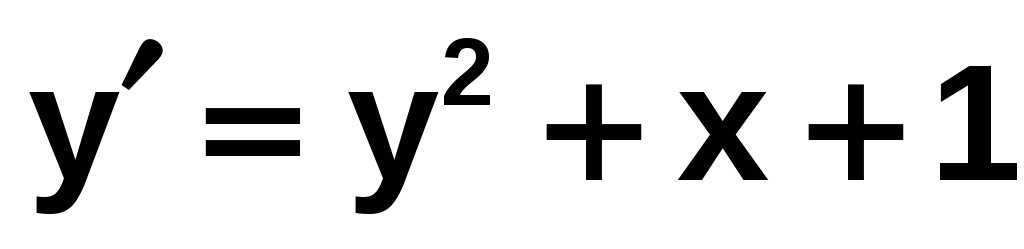 является...
является...-
обыкновенным дифференциальным уравнением 1-го порядка*
-
квадратным уравнением
-
интегральное уравнение
-
уравнение, содержащее производную
-
-
Порядок ОДУ это...
-
наивысший порядок производной, входящей в состав уравнения*
-
количество производных, входящих в состав уравнения
-
количество неизвестных, входящих в состав ОДУ
-
в списке нет правильного ответа
-
-
Аналитическое решение ОДУ 1-го порядка это...
-
функция y(x), которая при подстановке в уравнение, обращает его в тождество*
-

-
таблица значений искомой функции
-
в списке нет правильного ответа
-
-
Общим решением ОДУ
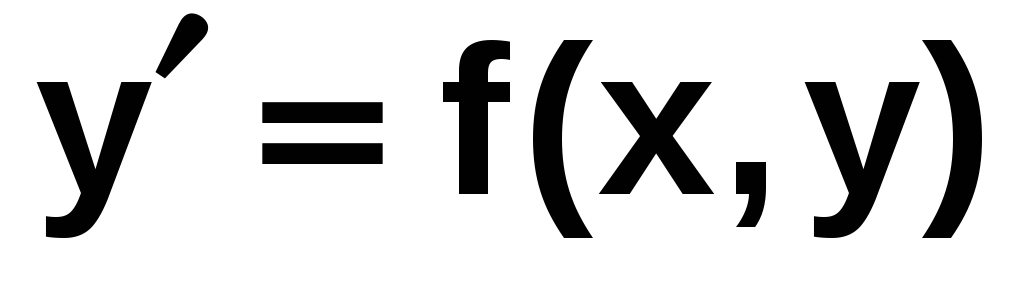 является...
является...
-
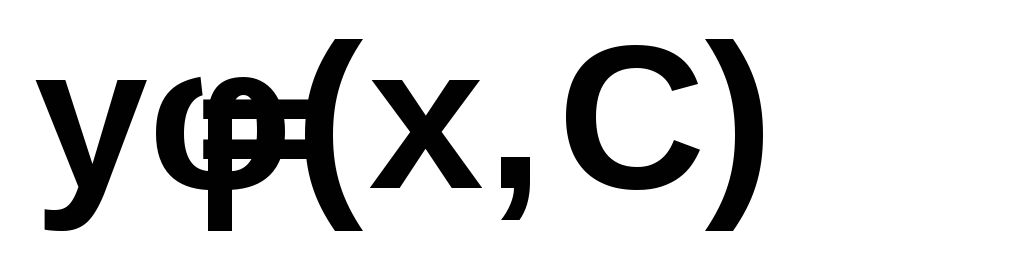 *
* -

-
таблица значений искомой функции
-
в списке нет правильного ответа
-
-
Геометрической интерпретацией общего решения ОДУ
 является...
является...-
семейство непересекающихся кривых*
-
две пересекающиеся кривые
-
две пересекающиеся прямые
-
в списке нет правильного ответа
-
-
Частным решением ОДУ
 является...
является...
-
 *
*
-
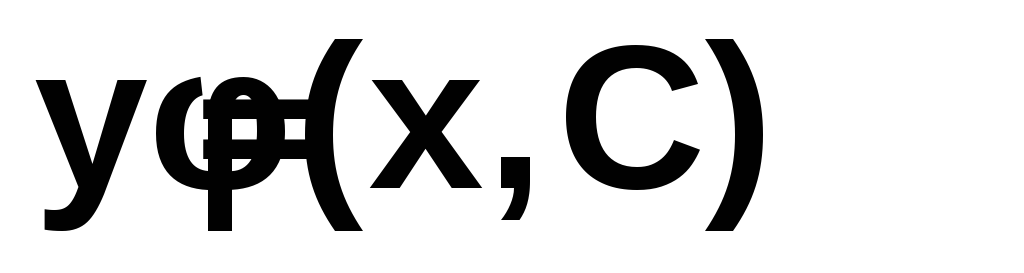
-
Таблица значений искомой функции
-
В списке нет правильного ответа
-
Численным решением ОДУ
 является...
является...-
таблица значений искомой функции*
-
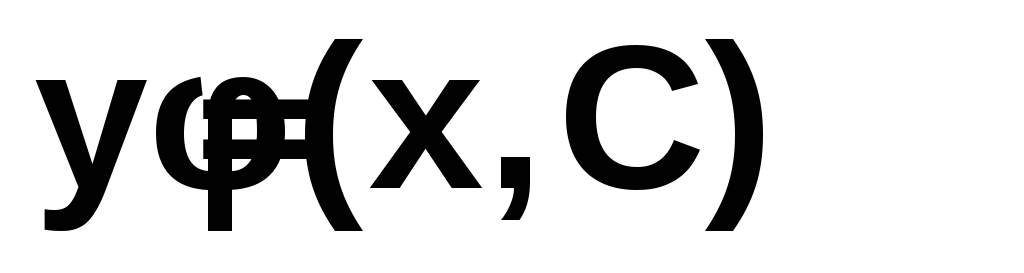
-

-
в списке нет правильного ответа
-
-
К начальным условиям при решении ОДУ 1-го порядка численными методами относятся...
-

-
 *
* -
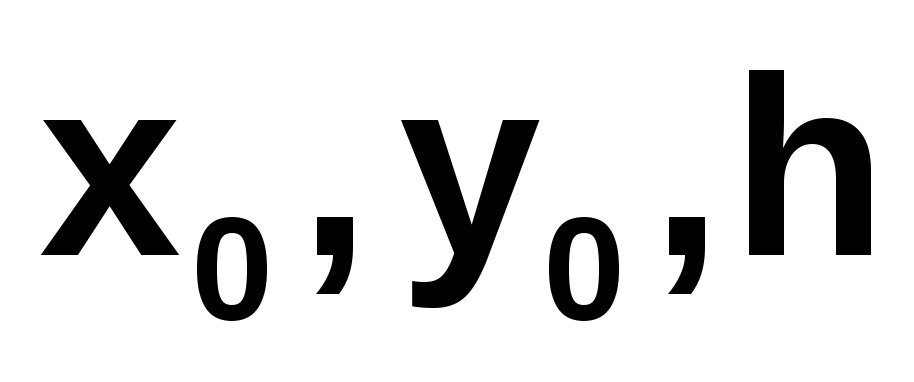
-
в списке нет правильного ответа
-
-
Задача Коши для дифференциального уравнения первого порядка имеет...
-
единственное решение*
-
не менее 2-х решений
-
ни одного решения
-
бесконечное множество решений
-
-
Не бывает методов Рунге-Кутта...
-
0-го порядка*
-
1-го порядка
-
2-го порядка
-
4-го порядка
-
-
Оценку погрешности решения методов Рунге-Кутты проводят...
-
по правилу Рунге*
-
по правилу Симпсона
-
по методу Лагранжа
-
по методу аппроксимации
-
-
 - эта формула является формулой для
определения очередного значения функции
по методу...
- эта формула является формулой для
определения очередного значения функции
по методу...-
Рунге-Кутты 1-го порядка*
-
Рунге-Кутты 2-го порядка
-
Рунге-Кутты 4-го порядка
-
в списке нет правильного ответа
-
-
Численные методы решения ОДУ позволяют...
-
вычислить приближенные значения искомого решения y(x) на некоторой сетке значений аргументов *
-
выразить решение ОДУ через элементарные функции
-
получить решение ОДУ как предел y(x) некоторой последовательности приближений
-
в списке нет правильного ответа
-
