Производная и дифференциал функции

Тема 1 Производная функции

1.1 Определение производной. Основные правила дифференцирования. Производная сложной и обратной функции

Пусть функция определена в некоторой окрестности точки .

Производной функции в точке называется предел отношения , когда (если этот предел существует). Производная функции в точке обозначается . Например, выражение следует понимать как производную функции в точке .

Дифференциал аргумента dx – приращение аргумента ∆х, дифференциал функции определяется как dy = y^/ dx

Определение производной можно записать в виде формулы

. (1)

Предел (1) может не существовать. В этом случае говорят, что функция не имеет производной в точке . Если предел (1) равен , то говорят, что функция имеет в точке бесконечную производную.

В различных задачах (в том числе и экономических) производная функции интерпретируется как скорость изменения величины y относительно x. Геометрический смысл производной состоит в том, что – это тангенс угла наклона касательной к графику в точке .

Нахождение производной функции называется дифференцированием этой функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке.

Укажем правила дифференцирования, которые сводят вычисление производных одних функций к вычислению производных других (более простых) функций.

Если функции дифференцируемы в точке , то сумма, разность, произведение и частное этих функций также дифференцируемы в точке , и справедливы следующие формулы

.

Если функция имеет обратную функцию и в точке производная , то обратная функция дифференцируема в точке и или .

Если функция дифференцируема в точке и , то сложная функция также дифференцируема в и верна следующая формула

или .

Производная неявной функции. Во многих задачах функция  y(x) задана невным образом. Например, для приведенных ниже функций

невозможно получить зависимость y(x) в явном виде. Алгоритм вычисления производной  y'(x) от неявной функции выглядит следующим образом:

• Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая, что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции;

• Решить полученное уравнение относительно производной  y'(x).

   Пример 1

Продифференцировать функцию y(x), заданную уравнением .

Решение. Продифференцируем обе части уравнения по переменной x:

     

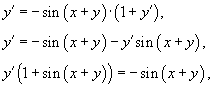
что приводит к результату:

1.2 Производные основных элементарных функций. Понятие о производных высших порядков. Эластичность функции

Используя определение непрерывности и определение производной функции в точке, замечательные пределы и правила дифференцирования можно показать, что производная каждой простейшей элементарной функции снова является элементарной функцией. Обычно производные основных элементарных функций сводятся в специальные таблицы:

1)

2)

3)

4)

5)

6)

7) .

Пусть – производная функции . Функция называется также первой производной. Производная функции называется второй производной функции и обозначается или . Вообще, п-ой производной функции называется производная ее (п-1)-ой производной: . Говорят также, что – это производная порядка п от функции . Теоретический анализ разнообразных явлений экономики использует ряд предельных величин: предельные издержки, предельный доход, предельная производительность, предельная полезность и т.д. Все эти величины тесным образом связаны с понятием производной. В качестве характерного примера рассмотрим характерные издержки.

Пусть х – количество произведенной продукции, – соответствующие данному выпуску издержки. Предельные издержки обозначим MY и определим как дополнительные издержки, связанные с производством еще одной единицы продукции, т.е.

, где .

Тогда

.

Предельные величины характеризуют не состояние, а процесс, изменение экономического объекта. Здесь производная означает скорость изменения некоторого экономического процесса во времени или относительно другого фактора. В этом заключается экономический смысл производной.

Для исследования прикладных экономических задач было введено понятие эластичности функции. По существу это понятие является чисто математическим и может применяться при анализе любых дифференцируемых функций. Эластичностью функции в точке х₀ называется следующий предел

.

Эластичность функции показывает приближенно, на сколько процентов изменится функция при изменении независимой переменной х на 1%.