Вариант 3

1. Дана расширенная матрица системы. Найти решение этой системы и соответствующей ей однородной системы.

.

2. Дана прямая . Составить уравнение прямой, проходящей через заданную точку М₀: а) параллельно данной прямой; б) перпендикулярно данной прямой. Исходные данные взять из таблицы 1.

3. Для матрицы третьего порядка вычислить ее определитель и найти обратную матрицу. Проверить правильность решения.

.

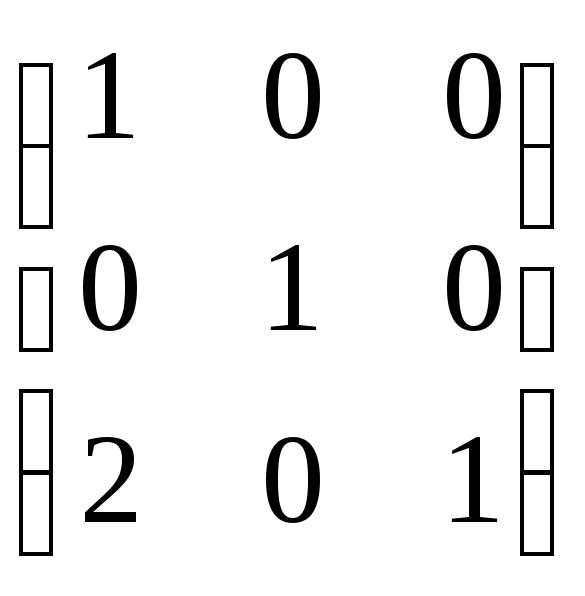4. Найти определитель четвертого порядка:

.

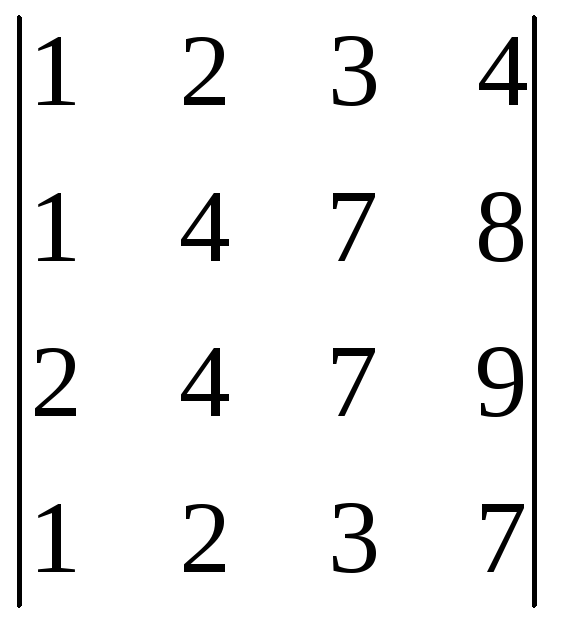5. Для прямых и найти их взаимное расположение. В случае их пересечения найти угол между ними, в случае параллельности – расстояние между ними. Исходные данные взять из таблицы 1.

6. Даны вершины треугольника с координатами (А, А₁), (В, В₁) и (С, С₁). Найти уравнения высоты и медианы этого треугольника. Исходные данные взять из таблицы 1.

7. Вычислить расстояние от точки М₁ до плоскости . Исходные данные взять из таблицы 1.

8. Найти угол между плоскостями и . Исходные данные взять из таблицы 1.

9. Написать уравнение прямой, проходящей через точки и Р. Исходные данные взять из таблицы 2.

10. Вычислить расстояние d от точки Р до прямой . Исходные данные взять из таблицы 2.

11. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

1) ; 2) .

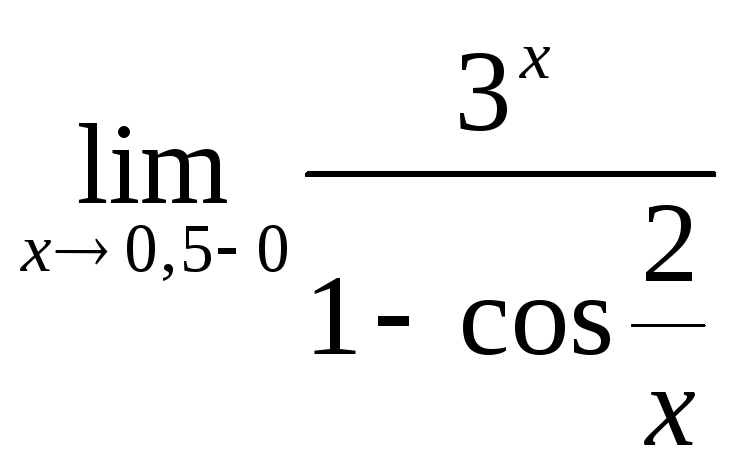12. Найти производные функций :

1) ; 2) ; 3) .

13. Найти интегралы:

1)

2)

3)

4)

5)

14. Найти площадь фигуры, ограниченной линиями:

1)	2) (внутри астроиды).

Вариант 4

1. Дана расширенная матрица системы. Найти решение этой системы и соответствующей ей однородной системы.

. .

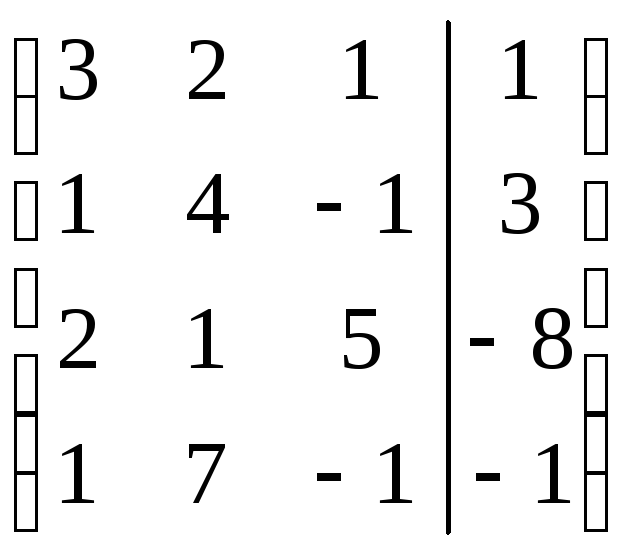2. Дана прямая . Составить уравнение прямой, проходящей через заданную точку М₀: а) параллельно данной прямой; б) перпендикулярно данной прямой. Исходные данные взять из таблицы 1.

3. Для матрицы третьего порядка вычислить ее определитель и найти обратную матрицу. Проверить правильность решения.

4. Найти определитель четвертого порядка:

.

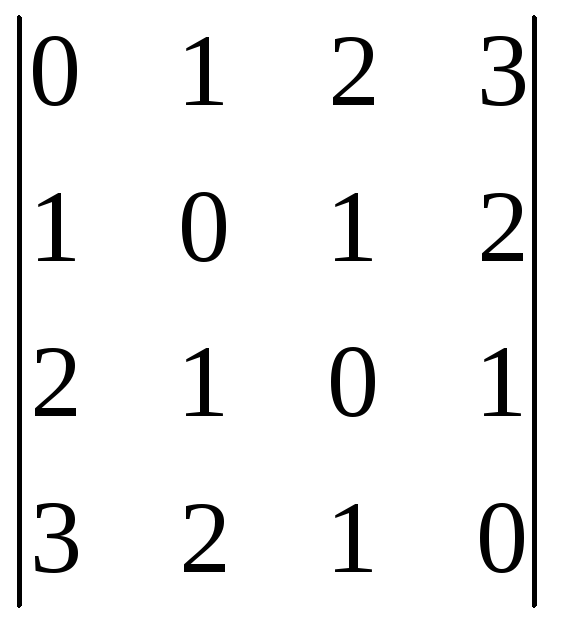5. Для прямых и найти их взаимное расположение. В случае их пересечения найти угол между ними, в случае параллельности – расстояние между ними. Исходные данные взять из таблицы 1.

6. Даны вершины треугольника с координатами (А, А₁), (В, В₁) и (С, С₁). Найти уравнения высоты и медианы этого треугольника. Исходные данные взять из таблицы 1.

7. Вычислить расстояние от точки М₁ до плоскости . Исходные данные взять из таблицы 1.

8. Найти угол между плоскостями и . Исходные данные взять из таблицы 1.

9. Написать уравнение прямой, проходящей через точки и Р. Исходные данные взять из таблицы 2.

10. Вычислить расстояние d от точки Р до прямой . Исходные данные взять из таблицы 2.

11. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

1) ; 2) .

12. Найти производные : 1) ; 2) ; 3)

13. Найти интегралы:

1)

2)

3)

4)

5)

14. Найти площадь фигуры, ограниченной линиями:

1)

2)