
- •Глава 3 Математические модели элементов электрических цепей
- •3.1. Классификация элементов электрических цепей
- •3.2. Способы описания свойств элементов электрических цепей
- •Рассмотрим подробнее свойства идеальных элементов электрических цепей.
- •3.3. Сопротивление
- •3.4. Емкость
- •3.5. Индуктивность
- •3.6. Индуктивно-связанная цепь или идеальный трансформатор
- •3.7. Активные элементы
- •3.8. Модели реальных пассивных элементов
- •3.9. Зависимые источники электрических сигналов
- •Контрольные вопросы
- •Глава 4 Электрические цепи при гармоническом воздействии в установившемся режиме
- •4.1. Способы описание электрических цепей
- •4.2. Законы Ома и Кирхгофа в комплексной форме
- •4.3. Эквивалентные преобразования электрических цепей
- •4.3.1. Эквивалентное преобразование схемы при последовательном соединении элементов
- •1) Эквивалентное преобразование сопротивлений
- •4.3.2. Эквивалентное преобразование схемы при параллельном соединении элементов
- •1)Эквивалентное преобразование сопротивлений
- •4.3.3. Эквивалентное преобразование схемы при смешанном соединении элементов
- •4.3.4. Эквивалентное преобразование источников электрических сигналов
- •4.4. Классификация электрических цепей
- •4.5. Воздействие, реакция, параметры и характеристики цепей.
- •4.6. Основные свойства линейных цепей
- •4.7. Основные свойства нелинейных цепей
- •4.8. Основные задачи теории электрических цепей
- •4.9. Методы анализа (расчета) линейных цепей при гармоническом воздействие
- •Метод комплексных амплитуд состоит в следующем:
- •4.9.1. Метод токов ветвей (мтв)
- •4.9.3. Метод узловых потенциалов (муп)
- •Контрольные вопросы
4.9.3. Метод узловых потенциалов (муп)
М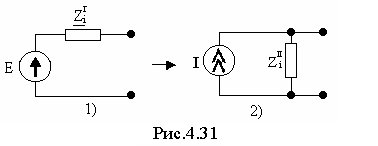 етод
основан на применение первого закона
Кирхгофа. В нем за неизвестные величины
принимают потенциалы узлов. Определив
по закону Ома определяют токи во всех
ветвях схемы.
етод
основан на применение первого закона
Кирхгофа. В нем за неизвестные величины
принимают потенциалы узлов. Определив
по закону Ома определяют токи во всех
ветвях схемы.
0) Все источники ЭДС, имеющиеся в схеме заменяют источниками тока (рис.4.31).
1) I=E/ Zi2
2) Zi1=Zi2
1) Топологический анализ.
а) Подсчитывается число ветвей I1, Iв, в=N
б) Нумеруют все
узлы. Один из узлов, к которому сходится
наибольшее число ветвей, считают нулевым,
где
![]() - потенциал нулевого узла.
- потенциал нулевого узла.
2.По 1-му закону Кирхгофа составляют уравнения для N-узлов схемы и решают их относительно потенциалов узлов.
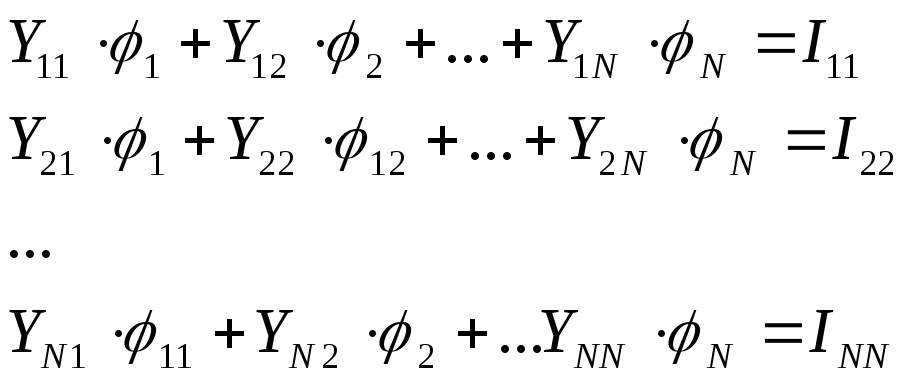
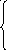
Yii-собственная узловая проводимость. Она равна сумме проводимостей всех ветвей, сходящихся в i-том узле, все они берутся со знаком «+».
Yij- межузловая проводимость между i-тым и j-тым узлами. Проводимости всех узлов берется со знаком «-».
Iii- алгебраическая сумма токов источников тока сходящихся в i-го узле. Втекающие токи записываются в эту сумму со знаком «+», а вытекающие – со знаком «-».
3) Потенциалы узлов находят по формуле Крамера.
![]() .
.
4) Токи в ветвях находят по закону Ома
I=(1-2)/Z.
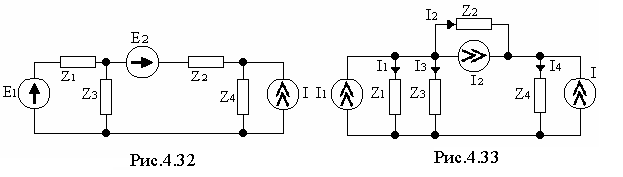
Пример. Дана электрическая цепь (рис.4.32). Рассчитать токи во всех ветвях.
 0).
Предварительно преобразуем все источники
напряжения (см. рис.4.32) в источники тока
(см. рис.4.33).
0).
Предварительно преобразуем все источники
напряжения (см. рис.4.32) в источники тока
(см. рис.4.33).
1). Проведем топологический анализ.
А). Число ветвей b=4; б). Число независимых узлов Nу=2, их потенциалы: φ1 и φ2 (см. рис. 4.33).
2). Составим систему уравнений по методу узловых потенциалов.
![]()
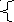 ,
,
![]() ;
;
![]() .
.
3). По методу Крамера
найдем потенциалы узлов
![]() .
.
4) По закону Ома
найдем токи во всех ветвях схемы:
![]()
Контрольные вопросы
каковы основные свойства линейных цепей.
1.Выполнение принципа суперпозиции и трансформация спектра. 2. Выполнение принципа суперпозиции и отсутствие трансформация спектра. 3.Не выполнение принципа суперпозиции. 4. Не выполнение принципа суперпозиции и трансформация спектра.
Какие узлы называются независимыми.
1. которые отличаются числом элементом в ветвях. 2. которые отличаются одной ветвью. 3. которые отличаются числом ветвей.
Какие контура называются независимыми.
1. которые отличаются числом элементом в ветвях. 2. которые отличаются одной ветвью. 3. которые отличаются числом ветвей.
Число независимых ветвей определяется из соотношения.
1. NУ= в-1. 2. NУ= у-1. 3. NУ= в-у+1.
Число независимых контуров определяется из соотношения.
1. NК= в-1. 2. NК= у-1. 3. Nк= в-у+1.
Показать запись закона Ома в комплексной форме.
1.
![]() .
2.
.
2.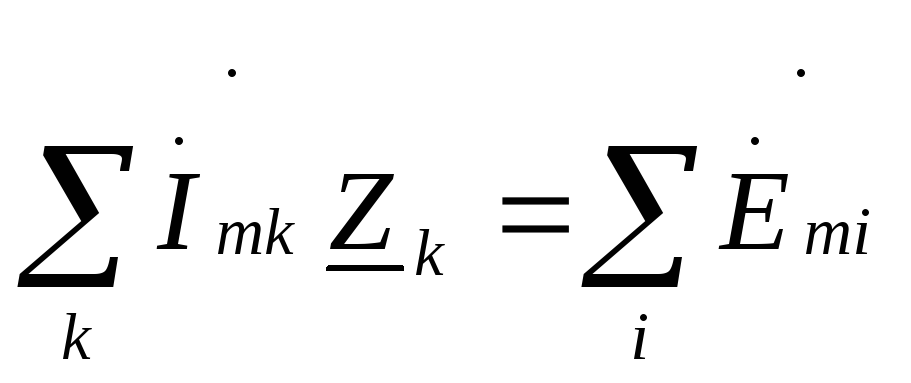 .
3. Ům=Zİm.
.
3. Ům=Zİm.
На каком законе основан метод контурных токов.
1. 1-ый закон Кирхгофа. 2. 2-ой закон Кирхгофа. 3.На законе коммутации для емкости. 4.На 1-ом и 2-ом законе Кирхгофа.
На каком законе основан метод узловых потенциалов.
1-ый закон Кирхгофа.
2-ой закон Кирхгофа.
На законе коммутации для емкости.
На 1-ом и 2-ом законе Кирхгофа.
З
 аписать
уравнения по методу контурных токов
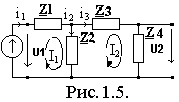
для схемы на рис.1.5.
аписать
уравнения по методу контурных токов
для схемы на рис.1.5.1.
2.
3.
(Z1+Z2)I1+Z3 I2=u1
Z3I1+(Z2+Z3 +Z4)i2=0
(Z1+Z2+Z3)I1+Z3 I2=u1
Z3I1+(Z2+Z3 +Z4)I2=0
(Z1+Z2)i1-Z3 i2=u1
-Z3i1+(Z2+Z3 +Z4)i2=0
Записать уравнение по методу узловых потенциалов для узла А схемы на рис.1.5.
1. φА((Z1-1+ Z2-1+ (Z3+ Z4)-1) = 0. 2. φА((Z1-1+ Z2-1+ (Z3+ Z4)-1) = U1/(Z1)
3. (Z1+Z2)I1+Z3 I2=u1 4. φА((Z1-1+ Z2-1+ (Z3+ Z4)-1) = E
Запишите второй закон Кирхгофа (для контура J1 на рис.1).
1. I1+I2+I3-I4-I5=0 2. I2+I3-I4-I5=0 3. I1R1+I2R2+I3R3=-I4-I5 4. I1+I2+I3-I4-I5=0 5. I3R2+I4R3 =E
З
 аписать
уравнение по методу узловых потенциалов
для узла А схемы на рис.1.
аписать
уравнение по методу узловых потенциалов
для узла А схемы на рис.1.
1. φА(R1-1+ R2-1+ R3-1+ R4-1) = 0;
2. φА(R1-1+ R2-1+ R3-1+ R4-1) = Е1(R1-1+ R2-1);
3. (R2+R3)J1-R2J2-R3J3=E1;
4. φА(R1-1+ R2-1+ R3-1+ R4-1)= Е1
Записать уравнения по методу контурных токов для схемы на рис.1.
1
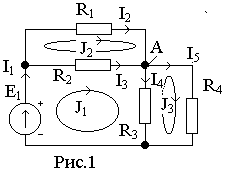 .
(R2+R3)J1-R2J2-R3J3=E1
.
(R2+R3)J1-R2J2-R3J3=E1-R2J1+(R1+R2)J2=0
-R3J1+(R3+R4)J3=0
2. (R2+R3)J1-R2J2-R3J3=E1
-R2J1+(R1+R2)J2=0
-R3J1-R2J2 +(R3+R4)J3=0
3. (R2+R3)J1-R2J2-R3J3=E1
(R2+R3)J1-R2J2+(R1+R2)J2=0
-R3J1+(R3+R4)J3=0
4. (R2+R3)J1-R2J2-R3J3=E1
-R2J1+(R1+R2)J2= E1
-R3J1+(R3+R4)J3=0
Для независимых узлов схемы на рис.1 записать уравнения по 1-ому закону Кирхгофа.
I1 – I2 - I3= 0
I2+I3 - I4-I5= 0
I4+I5 – I1=0
I1 + I2 - I3= 0
I2+I3 - I4-I5= 0
I4+I5 – I1=0
I1 – I2 - I3= 0
I2+I3 - I4 - I5= 0
I1 + I2 + I3= 0
I2+I3 - I4 - I5= 0
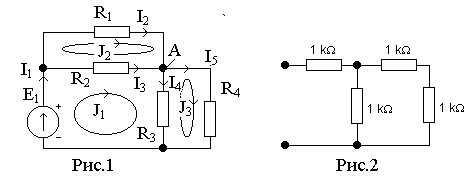
Подсчитать эквивалентное входное сопротивление цепи (рис.2).
1. 1кОм. 2. 5/3кОм. 3. 2кОм 4.3кОм.
