8.4.1. Схемы звеньев фильтра

Избирательные свойства звеньев фильтра и фильтра в целом объясняются тем, что в их схему входят элементы (катушки индуктивности и емкости) сопротивления которых зависят от частоты.

1. Для простейшей г-образной схемы с комплексными сопротивлениями z1 и z2, коэффициент передачи по напряжению определяется выражением

2. .

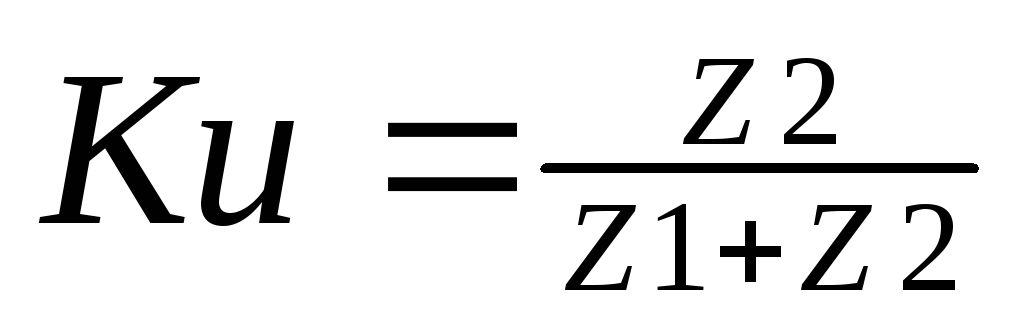Отсюда следует, что на частотах когда |Z2|>>|Z1|, то Кu→1 это полоса пропускания. На тех частотах, когда |Z2|<<|Z1|, то Кu→0, это полоса заграждения.

Рассмотрим конкретные схемы звеньв фильтра.

1) Простейшие схемы однозвенных ФНЧ приведены на рис.8.5.

На рис.8.5 а, б и в приведены Г-образные схемы, соответственно, RC-типа, 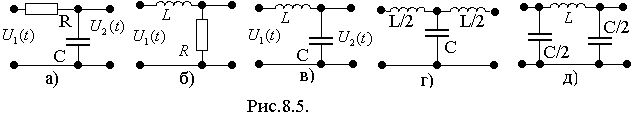RL-типа и LC-типа типа, а на рис.8.5 г, д приведены схемы Т- и П-образные схемы на LC-элементах. Работа, например, фильтра RC-типа, происходит следующим образом. Если ω→0, то сопротивление конденсатора (1/ωС)→∞, а следовательно U_2m = U_1m , т.е. сигнал передается через цепь без ослабления. При увеличении частоты входного сигнала сопротивление конденсатора уменьшается, (1/ωС)→0. Амплитуда выходного напряжения на конденсаторе |U_2m|→0 и, следовательно, высокочастотный сигнал через фильтр не проходит, т.е. подавляется.

Комплексный коэффициент передачи по напряжению K_u(j)=U_2m/U_1m, и амплитудно-частотная характеристика (АЧХ) - K_u()=U_2m/U_1m , рассмотренного ФНЧ определяются из выражений

К_u(jω)=(1+jω RC)^-2, К_u(ω)=(1+(ωRC)²)^-2.

2) Простейшие схемы однозвенных ФВЧ приведены на рис.8.6.

На рис.8.6 а, б и в приведены Г-образные схемы, соответственно: RC-типа, RL-типа и LC-типа, а на рис.8.5 г, д приведены схемы Т- и П-образные схемы на LC-элементах. Работа, например, фильтра RC-типа, происходит следующим образом. Если ω→0, то сопротивление конденсатора (1/ωС)→∞, а следовательно U_2m→0, т.е. низкочастотный сигнал через фильтр не проходит, т.е. подавляется. При увеличении частоты входного сигнала сопротивление конденсатора уменьшается (1/ωС)→0, следовательно, U_2m = U_1m , т.е. высокочастотный сигнал передается через цепь без ослабления.

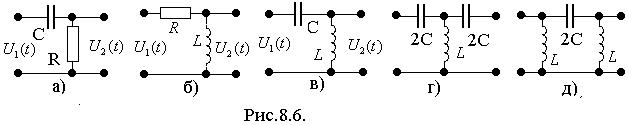
3) Полосно-пропускающий фильтр (ППФ) можно получить путем последовательного соединения двух звеньев ФНЧ и ФВЧ, подобрав соответствующим образом их граничные частоты.

О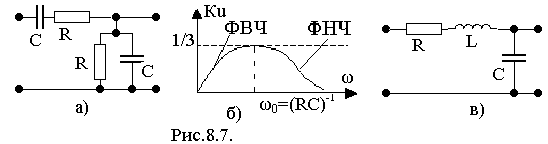днако на практике, часто, используют схему моста Вина (рис.8.7а). На рис. 8.7б приведена зависимость его коэффициента передачи от частоты. На рис.8.7в приведена схема ППФ на основе последовательного контура.

4) Полосно-заграждающий фильтр (ПЗФ) можно получить путем последовательного соединения ФНЧ и ФВЧ при соответствующем выборе граничных частот.

Однако на практике, часто, используют схему двойного Т-образного моста (рис.8.7а). Зависимость коэффициента передачи от частоты этой схемы приведена на рис. 8.7б. Аналогичной характеристикой обладает схема на основе последовательного контура (рис.8.7в).

8.4.2. Влияние числа звеньев фильтра на его характеристики

Рассмотрим это влияние на сравнении одно- и двух-звенного ФНЧ на RC элементах (рис.8.9а, б). Будем считать, что в состав второй схемы(рис.8.9б), между звеньями, входит устройство согласования звеньев по сопротивлениям. Согласующий каскад [x1] имеет большое входное (Rвх) и малое выходное (Rвых0) сопротивления, при этом его коэффициент передачи равен единице (Кu =1). Это позволяет считать 1-ое и 2-е звено независимыми.

Д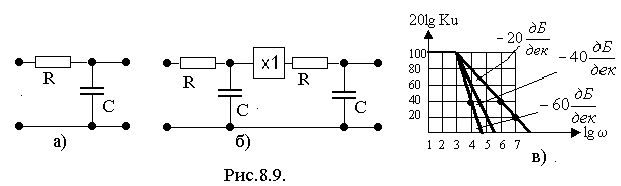ля первой схемы комплексный коэффициент передачи по напряжению и его АЧХ определяются из выражений

, .

Граничная частота звена определяется из соотношения _гр=1/(RC). В полосе заграждения, при >_гр, коэффициент передачи убывает со скоростью K_u()  1/, т.е., при увеличение  в 10 раз K_u() убывает в 10 раз. Это убывание в логарифмических единицах составляет величину 20 дБ на декаду, т.е. V= - 20дБ/дек.

Фильтр с одним реактивным элементом называется фильтром первого порядка поскольку он описывается дифференциальным уравнением 1-го порядка.

Рассмотрим АЧХ комплексного коэффициента передачи по напряжению для двухзвенного фильтра. Она определяется как произведение коэффициентов передач звеньев

Ku()=К₁К₂=.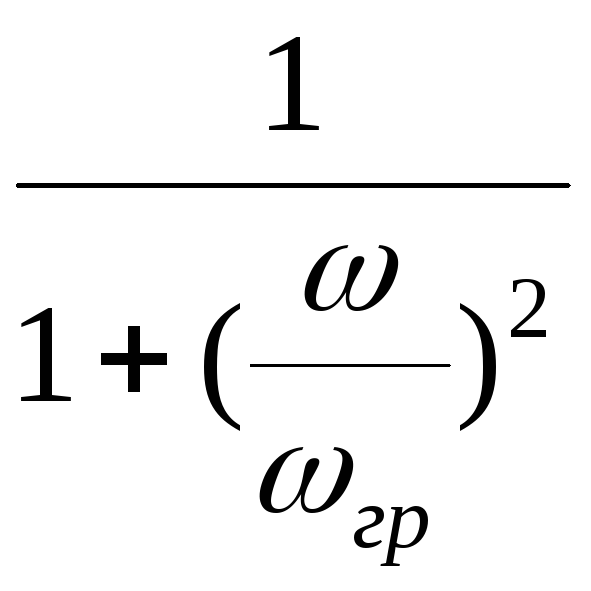

При > ω _гр, Ku()1/² т.е. = - 40.

Вывод. Чем больше звеньев в фильтре, тем выше скорость спада в полосе заграждения (V) и тем фильтр ближе к идеальному. При независимых звеньях скорость спада составляет V=n20 дБ/дек, где n – число звеньев.