5.3. Частотные характеристики

Поскольку сопротивления элементов цепей зависят от частоты, то параметры цепей оказываются частотно-зависимыми. Зависимости параметров цепей от частоты называют частотными характеристиками (ЧХ) или частотными функциями цепи.

Каждый параметр цепи имеет свою частотную характеристику ЧХ. Название ЧХ дают в соответствии с названием параметра. Например: ЧХ входного сопротивления, ЧХ коэффициента передачи напряжения.

ЧХ есть зависимость от частоты отношения комплексной амплитуды отклика к комплексной амплитуде воздействия. Как всякую комплексную функцию ее можно записать в одной из трех форм записи: показательной, алгебраической и тригонометрической (последняя, применяется редко).

.

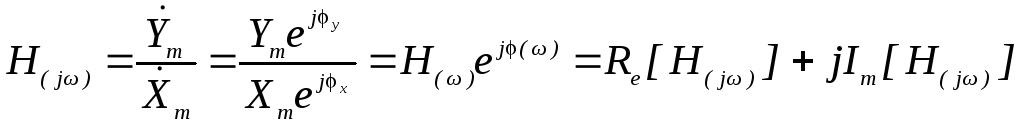H(ω)=Y_m/X_m - амплитудно-частотная характеристика (АЧХ) или ее называют модуль комплексной функции – mod[H(jω)] =.

АЧХ – есть зависимость от частоты отношения амплитуды гармонического сигнала на выходе к амплитуде гармонического сигнала на входе (без учета начальных фаз).

- фазо-частотная характеристика (ФЧХ) или ее называют аргументом комплексной функции – arg[H(jω)] = .

ФЧХ – есть зависимость от частоты сдвига по фазе между выходным и входным сигналами.

,,- реальная и мнимая составляющие ЧХ электрической цепи.

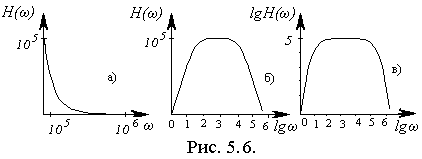
Для наглядности ЧХ цепей представляют в виде графиков. Графики строят двумя способами.

1. ЧХ можно представлять в виде двух графиков –АЧХ и ФЧХ.

При построении графиков АЧХ и ФЧХ пользуются следующими масштабами по осям: абсолютным или линейным и логарифмическим. На рис.5.6а приведен график в абсолютном линейном масштабе, на рис.5.6б в полулогарифмическом масштабе, а на рис.5.6в в логарифмическом масштабе.

2. ЧХ можно представить на одном графике. График комплексной функции, построенный в одной системе координат, называют годографом. Годограф – это геометрическое место точек, которые описывает конец вектора комплексной функции на комплексной плоскости при изменении частоты от 0 до бесконечности.

Для построения годографа обычно используют алгебраическую форму записи 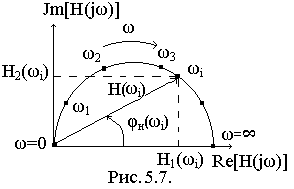частотной характеристики Н(jω) = Re[Н(jω)] + jJm[Н(jω)]. Далее для определенных частот ω_i рассчитывают значения Re[Н(jω)] = Н₁(ω_i) и Jm[Н(jω)] = Н₂(ω_i), и составляют таблицу данных, а затем, как обычно, наносят эти точки на плоскость и соединив их получают график годографа (рис.5.7).

Таблица данных для построения АФХ Таблица 1.1.

Частота f, Гц	Re[Н(jω)] = Н1(ωi)	Jm[Н(jω)] = Н2(ωi)

5.4. Примеры расчёта частотных характеристик цепей

Пример 1. Для обобщенной одноконтурной цепи, представленной комплексной схемой замещения (рис.5.8) рассчитать ее частотные характеристики.

1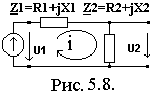. Z_вх(j), Z_вх(), _z(). 2. K(j), K(), _k().

Решение. 1) По определению Z_вх(j)=Ů_1m/.Используя законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления:

Z_вх(j)=Ů_1m/Ĭ_1m= Ĭ_1m(Z₁+Z₂)/ Ĭ_1m =(R₁+R₂)+j(X₁+X₂)=R+jX;

Z_вх()=[(R₁+R₂)²+(X₁+X₂)²]^1/2; _z()=arctg[(X₁+X₂)/(R₁+R₂)].

2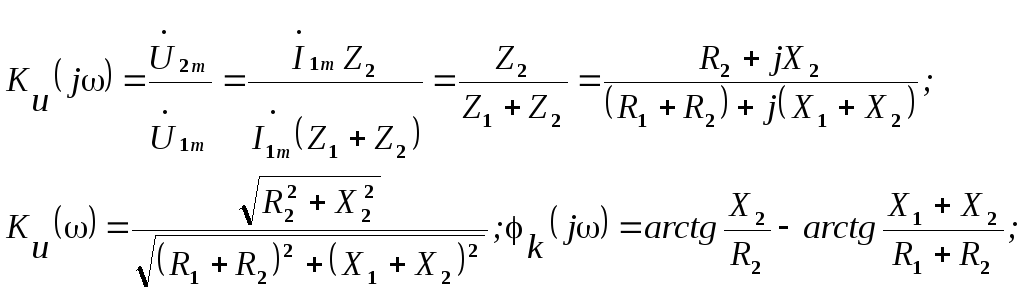) Используя определение К(j) и законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ коэффициента передачи по напряжению:

Пример 2. Для цепи изображенной на рис.5.9 рассчитать:

zвх(j), z(), _z().

K_U(j), K(), _K().

От исходной цепи переходим к ее комплексной схеме замещения. Она соответствует схеме на рис.5.8.

И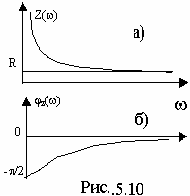спользуя, определениеz_вх(j) и законы Ома и Кирхгофа получим его выражение

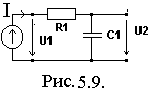
Определим АЧХ и ФЧХ для z_вх(j) и построим их графики (рис.5.10.), подсчитав значения при =0, =.

; Zвх(0) = . Zвх() = R.

_z()= -arctg ,_z(0)=-/2, _z()=0.

Используя, определение K_U(j) получим его выражение K_u(j)====.

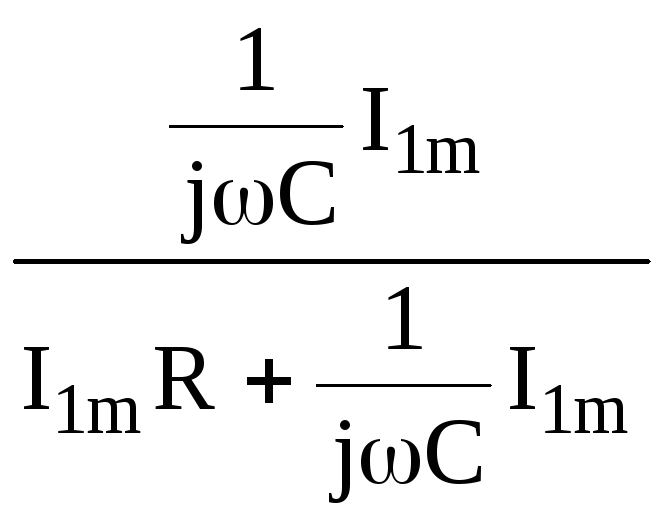Определим АЧХ и ФЧХ для Ku (j) и построим их графики (рис.5.11.), подсчитав значения при =0, =.

Вспомним, что z==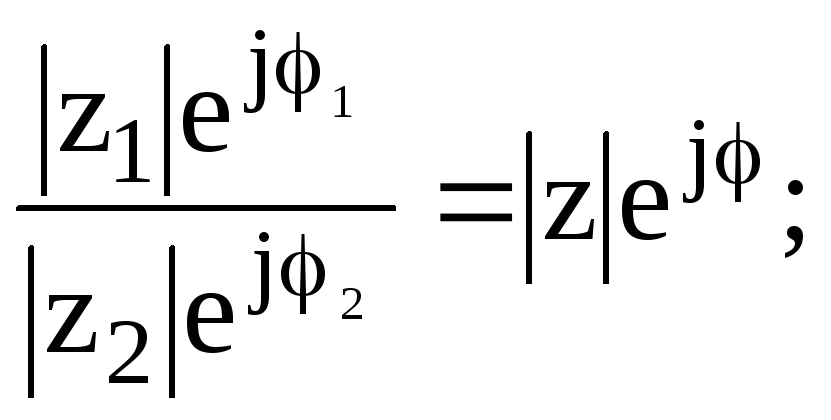где:тогда,

Ku(0)=1; Ku()=0.

Отсюда следует: φ_к()= π/2, φ_к(0)= 0.

Такая цепь пропускает сигналы низких частот (Ku(0)=1) и подавляет сигналы высоких частот (Ku()=0) и называется фильтром низких частот (ФНЧ).

Граничная частота определяется из выражения . Рассчитаем ее для нашего примера:

, _грRC=1 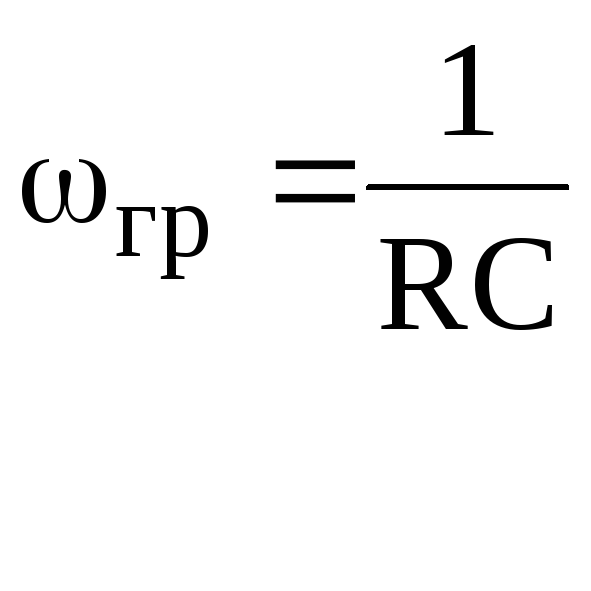 . Построить годограф частотно-передаточной функции (годограф иногда называют АФЧХ).

При .

При

Учитывая, что реальная часть всегда положительна и уменьшается от 1 до 0, а мнимая часть всегда отрицательна, можно построить график годографа (рис. 5.12.).

П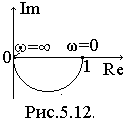ример 3. Для обобщенной двухконтурной цепи, представленной комплексной схемой замещения (рис.5.13), рассчитать ее частотные характеристики:

1. Z_вх(j), Z_вх(), _z(). 2.K(j), K(), _k().

Решение. 1) Найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления.

П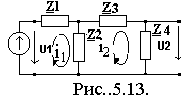о определению Z_вх(j)=Ů_1m/.Входное сопротивление находимметодом последовательных эквивалентных преобразований. Этот метод состоит в поэтапном преобразовании простых участков цепи. Они показаны на рис.5.14.

2. найдем КЧХ коэффициента передачи по напряжению. По определения K_u(j)=Ů_2m/Ů_1m , а Ů_2m=Z₄İ₂ – находим по закону Ома.

Отсюда видно, что для расчета КЧХ необходимо найти İ₂. Находим İ₂ методом контурных токов. Для этого: определим число независимых контуров: N_k=в-у+1=3-2+1=2, каждому из них присвоим свой контурный ток İ₁, İ₂ и составим уравнения по методу контурных токов.

Z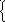₁₁İ₁+Z₁₂İ₂=E₁₁

Z₂₁İ₁+Z₂₂İ₂=E₂₂ ,

где: Z₁₁ – собственное сопротивление первого контура, Z₁₁=Z₁+Z₂;

Z₁₂ и Z₂₁ сопротивление смежных контуров, Z₁₂= Z₂₁= - Z₂ ;

Z₂₂-собственное сопротивление II контура. Z₂₂=Z₂+Z₃+Z₄ ;

Ė₁₁-алгебраическая сумма источников ЭДС I-ого контура, Ė₁₁=U_1m;

E₂₂- алгебраическая сумма источников ЭДС II-ого контура, во II контуре источников ЭДС нет, Ė₂₂=0.

Найдем İ ₂- ток второго контура (по методу Крамера), а затем и КЧХ коэффициента передачи по напряжению:

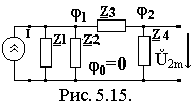
Покажем другой способ нахождения КЧХ коэффициента передачи по напряжению. Найдем КЧХ, используя для расчета U_2m метод узловых потенциалов. Для этого:

• преобразуем исходную схему к виду, показанному на рис.5.15, заменив источник эдс на источник тока;

• потенциал узла 0 примем равным нулю, ₀=0;

• тогда Ů_2m=₂ - ₀= _2.

Составив уравнения по методу узловых потенциалов, получим систему второго порядка и решим ее, относительно ₂, по методу Крамера:

Y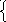₁₁₁+ Y₁₂₂=I₁₁

Y₂₁₁+ Y₂₂₂=I₂₂,

где: Y_{11 –} собственная проводимость первого узла, Y₁₁=(1/Z₁)+(1/Z₂)+(1/Z₃);

Y₁₂ и Y₁₂ – межузловая проводимость Y₁₂= Y₂₁= - 1/Z₃; =-1/Z₃;

Y₂₂ - собственная проводимость первого узла Y₂₂=(1/Z₃) +(1/Z₄);

_1, ₂ – потенциалы первого и второго узлов;

I_11, I₁₁ – токи источников токов сходящихся в первом и втором узлах.