
- •Глава 5
- •5.2. Параметры четырехполюсника
- •5.3. Частотные характеристики
- •5.4. Примеры расчёта частотных характеристик цепей
- •Отсюда следует, что
- •5.5. Резонансные цепи. Колебательные контуры
- •5.5.1. Последовательный колебательный контур
- •5.5.1.2. Зависимость добротности контура q от сопротивления источника сигнала (Ri) и сопротивления нагрузки (Rн)
- •5.5.1.3. Последовательный колебательный контур как четырехполюсник
- •5.5.2. Параллельный колебательный контур
- •5.5.2.1. Резонансная характеристика параллельного колебательного контура
- •5.5.2.2. Влияние сопротивлений источника сигнала и нагрузки на добротность параллельного колебательного контура
- •5.6. Связанные колебательные контуры
- •5.6.1. Резонанс в связанных колебательных контурах
- •5.7. Операторные функции цепи
- •Контрольные вопросы
- •Глава 6 Импульсные сигналы в линейных цепях
- •6.1. Импульсные сигналы в линейных цепях
- •6.2. Временные характеристики цепей
- •6.3. Понятия о переходных процессах в электрических цепях и Понятие о коммутации
- •6.4. Методы анализа линейных цепей при импульсном воздействии
- •6.4.1. Классический метод анализа
- •6.4.2. Спектральный метод анализа
- •6.4.3. Операторный метод анализа Операторный метод расчета переходных процессов
- •6.4.4. Метод интеграла Дюамеля
- •6.5. Передача импульсных сигналов через простейшие цепи
- •6.5.1. Передача импульсных сигналов через дифференцирующую цепь
- •6.5.2. Передача импульсных сигналов через интегрирующую цепь
- •Коэффициенты р находят, как корни характеристического уравнения
- •6.6. Пример расчета переходной характеристики двухконтурной цепи
- •Коэффициенты находят, как корни характеристического уравнения:
- •6.7. Расчет переходных характеристик последовательного колебательного контура
- •Коэффициенты находят, как корни характеристического уравнения:
- •6.8. Связь между дифференциальным уравнением и характеристиками электрической цепи
- •Контрольные вопросы
6.5.2. Передача импульсных сигналов через интегрирующую цепь
Цепь, состоящая из RC элементов и приведенная на рис.6.15. называется интегрирующей RC-цепью.
Установим
связь между выходным u2
и входным u1
напряжениями,
считая входной сигнал u1произвольным.
Используя, второй закон Кирхгофа и
соотношения между напряжениями и токами
на элементах схемы, запишем


Подставим полученные напряжения в первое выражение
![]() .
.
Если R![]() >>
>>![]() ,
тоR
,
тоR![]() =
=![]() ;
или
;
или![]()
Последнее означает, что выходной сигнал есть интеграл от входного сигнала. Отсюда и название этой цепи – интегрирующая цепь.
Рассмотрим, по входному сигналу, два частных случая.
А. Пусть входной
сигнал - ступенчатое напряжение амплитудой
Е (рис.6.9)
![]() .
Используя классический метод, определим
отклик цепи.
.
Используя классический метод, определим
отклик цепи.
Составим дифференциальное уравнение и приведем его к стандартному виду:
 .
.
2) Запишем общее решение.
![]() .
.
3) Найдем вынужденную
составляющую общего решения -
![]() .
.
Вынужденную
составляющую находим в стационарном
(установившемся) режиме, который имеет
место когда, t
∞.
В этом случае входной сигнал – постоянное
напряжение величины
![]() ,
ему соответствует гармонический сигнал
с н
,
ему соответствует гармонический сигнал
с н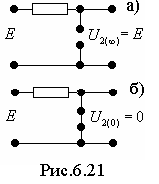 улевой
частотой
ω=0,т.к.,
улевой
частотой
ω=0,т.к.,![]() =
=![]() cosωt\
(ω=0)
. При таких
условиях наличие индуктивности
равносильно короткому замыканию (ХL=
ωL),
а емкости – разрыву цепи (ХС=
(ωС)-1).
cosωt\
(ω=0)
. При таких
условиях наличие индуктивности
равносильно короткому замыканию (ХL=
ωL),
а емкости – разрыву цепи (ХС=
(ωС)-1).
Для нахождения вынужденной составляющей составим схему замещения исходной цепи при ω=0 (см. рис.6.16а). Из схемы следует, что u2(∞)=Е.
4) Найдем показатель экспоненты - р1.
Коэффициенты р находят, как корни характеристического уравнения
RCр1+1=0. Отсюда р 1= - (RC)-1.
5) Найдем постоянную интегрирования A1.
Ее находим из общего решения при t0 и схемы замещения исходной цепи при t0, ω ∞. Она приведена на рис. 6.16б. Запишем уравнение откуда и найдем А1
![]() ,
А1=
- Е.
,
А1=
- Е.
6) Запишем общего решение:
![]() .
.
Выходное напряжение представляет собой импульс, нарастающий по экспоненте, который характеризуется двумя параметрами:

1. Е – амплитуда импульса;
2. τ - постоянная времени цепи.
Определим выходной сигнал при t=τ.
![]()
Отсюда следует, что постоянная времени это время за которое импульс возрастая по экспоненциальному закон изменяется от 0 до уровня 0,63 от своего стационарного значения Е.
Иногда пользуются третьим параметром. tуст. – время установления выходного напряжения, это время за которое сигнал достигает свое стационарное значение, с заданной точностью от амплитуды импульса. Так время установление на уровне 0,9 и 0,95 составляет tуст.0.9 =2,3τ; tуст.0.95 =3τ.
Б. Пусть входной сигнал одиночный прямоугольный импульс (рис.6.18) амплитудой Е и длительностью tu. Такой импульс представляет собой суперпозицию двух ступенчатых сигналов и записывается как
![]() .
.
Зная отклик на ступенчатый сигнал, и используя принцип суперпозиции можно записать аналитическое выражение для выходного сигнала:
![]()
На рис 6.19 показаны
три временных диаграммы выходного
сигнала при
 различных
соотношения между τ и tи.
различных
соотношения между τ и tи.
Аналогичными свойствами обладает цепь, состоящая из RL элементов, приведенная на рис.6.20. Она называется интегрирующая RL-цепь.
6.6. Пример расчета переходной характеристики двухконтурной цепи
Дана
двухконтурная цепь (рис.6.21), рассчитать
ее переходную характеристику
![]() .
.
З адачу
будем решать классическим способом. За
переменную в составляемом уравнении
выбираем переменную, характеризующую
энергетическое состояние цепи, которая
наиболее просто связана с выходным
сигналом.
адачу
будем решать классическим способом. За
переменную в составляемом уравнении
выбираем переменную, характеризующую
энергетическое состояние цепи, которая
наиболее просто связана с выходным
сигналом.
Такой переменной является ток через индуктивность iL, он связан с выходным напряжением соотношением
![]() .
.
1) составим дифференциальное уравнение и приведем его к стандартному виду. При составлении уравнений относительно тока iL=i2 воспользуемся, метод контурных токов (здесь i1 и i2 – токи соответственно первого и второго контура) и составим два уравнения для первого и второго контура
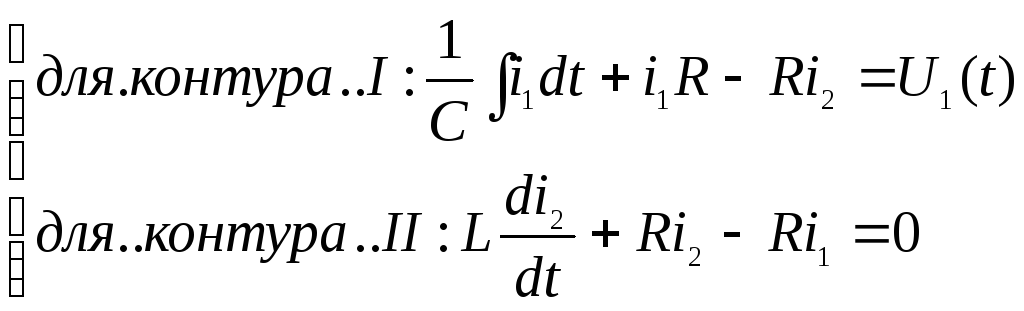
Из
второго уравнения найдем ток первого
контура
![]() и подставим его выражение в первое
уравнение, полученное выражение поделим
наL
и продифференцируем по времени
и подставим его выражение в первое
уравнение, полученное выражение поделим
наL
и продифференцируем по времени
![]()
![]() ;
;
введем обозначения (RC)-1=2β, (LC)-1=ω0 , получим
![]()
2) Запишем общее решение относительно тока второго контура и входного напряжения.
![]()

![]() ;
;
3) Найдем вынужденную
составляющую общего решения -
![]() .
.
Вынужденную
составляющую находим в стационарном
(установившемся) режиме, который имеет
место когда, t
∞.
В этом случае входной сигнал – постоянное
напряжение величины
![]() ,
ему соответствует гармонический сигнал
с нулевой частотой
ω=0,т.к.,
,
ему соответствует гармонический сигнал
с нулевой частотой
ω=0,т.к.,![]() =
=![]() cosωt\
(ω=0)
. При таких
условиях наличие индуктивности
равносильно короткому замыканию (ХL=
ωL),
а емкости – разрыву цепи (ХС=
(ωС)-1).
cosωt\
(ω=0)
. При таких
условиях наличие индуктивности
равносильно короткому замыканию (ХL=
ωL),
а емкости – разрыву цепи (ХС=
(ωС)-1).
Для нахождения вынужденной составляющей составим схему замещения исходной цепи при ω=0 (см. рис.6.22а). Из схемы следует, что i2(∞)=0.
4) Найдем показатели экспоненты - р1 и p2.
