
- •Глава 5
- •5.2. Параметры четырехполюсника
- •5.3. Частотные характеристики
- •5.4. Примеры расчёта частотных характеристик цепей
- •Отсюда следует, что
- •5.5. Резонансные цепи. Колебательные контуры
- •5.5.1. Последовательный колебательный контур
- •5.5.1.2. Зависимость добротности контура q от сопротивления источника сигнала (Ri) и сопротивления нагрузки (Rн)
- •5.5.1.3. Последовательный колебательный контур как четырехполюсник
- •5.5.2. Параллельный колебательный контур
- •5.5.2.1. Резонансная характеристика параллельного колебательного контура
- •5.5.2.2. Влияние сопротивлений источника сигнала и нагрузки на добротность параллельного колебательного контура
- •5.6. Связанные колебательные контуры
- •5.6.1. Резонанс в связанных колебательных контурах
- •5.7. Операторные функции цепи
- •Контрольные вопросы
- •Глава 6 Импульсные сигналы в линейных цепях
- •6.1. Импульсные сигналы в линейных цепях
- •6.2. Временные характеристики цепей
- •6.3. Понятия о переходных процессах в электрических цепях и Понятие о коммутации
- •6.4. Методы анализа линейных цепей при импульсном воздействии
- •6.4.1. Классический метод анализа
- •6.4.2. Спектральный метод анализа
- •6.4.3. Операторный метод анализа Операторный метод расчета переходных процессов
- •6.4.4. Метод интеграла Дюамеля
- •6.5. Передача импульсных сигналов через простейшие цепи
- •6.5.1. Передача импульсных сигналов через дифференцирующую цепь
- •6.5.2. Передача импульсных сигналов через интегрирующую цепь
- •Коэффициенты р находят, как корни характеристического уравнения
- •6.6. Пример расчета переходной характеристики двухконтурной цепи
- •Коэффициенты находят, как корни характеристического уравнения:
- •6.7. Расчет переходных характеристик последовательного колебательного контура
- •Коэффициенты находят, как корни характеристического уравнения:
- •6.8. Связь между дифференциальным уравнением и характеристиками электрической цепи
- •Контрольные вопросы
6.4.4. Метод интеграла Дюамеля
О н
позволяет находить отклик цепи при
нулевых начальных условиях при
произвольном входном сигнале и известной
переходной (импульсной) характеристики
цепи (рис.6.6).
н
позволяет находить отклик цепи при
нулевых начальных условиях при
произвольном входном сигнале и известной
переходной (импульсной) характеристики
цепи (рис.6.6).
П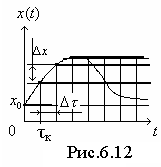 роизвольный
импульсный сигнал (рис.6.7.) заменим
совокупностью элементарных ступенчатых
сигналов с амплитудами ∆х, возникающими
в моменты времени τк
со сдвигом по времени на
роизвольный
импульсный сигнал (рис.6.7.) заменим
совокупностью элементарных ступенчатых
сигналов с амплитудами ∆х, возникающими
в моменты времени τк
со сдвигом по времени на
![]() .
.
Как следует из
рисунка х0
- амплитуда
нулевого ступенчатого сигнала. Тогда
отклик на него
![]() ;
;
![]() - амплитуда
элементарного ступенчатого сигнала,
рассчитывается из выражения
- амплитуда
элементарного ступенчатого сигнала,
рассчитывается из выражения
![]() ,
где х'(τк)
– производная от сигнала в момент
времени τк,,
она равна тангенса угла наклона сигнала
в момент времени τк.
Тогда, отклик на элементарный ступенчатый
сигнал равен
,
где х'(τк)
– производная от сигнала в момент
времени τк,,
она равна тангенса угла наклона сигнала
в момент времени τк.
Тогда, отклик на элементарный ступенчатый
сигнал равен
![]() .
.
Используя принцип суперпозиции и переходя к пределу суммы при Δτ→0 (Δτ=dτ) можно записать что
![]() .
.
Последнее выражение и называется интегралом Дюамеля. Оно позволяет получить отклик на заданное воздействие в любой момент времени t после коммутации. Интегрирование ведется по τ – текущее время (0<τ<t), причем выражения х'(τ) и h(t- τ) получают из выражений для х(t) и h(t) путем замены t на τ и t- τ.
6.5. Передача импульсных сигналов через простейшие цепи
Электрические цепи служат для связи различных устройств между собой, при этом обычно ставится задача неискаженной передачи сигнала. В ряде случаев электрические цепи применяют для преобразования сигналов одной формы в другую.
6.5.1. Передача импульсных сигналов через дифференцирующую цепь
Ц епь,
состоящая изRC
элементов и приведенная на рис.6.8.
называется дифференцирующей RC-цепью.
епь,
состоящая изRC
элементов и приведенная на рис.6.8.
называется дифференцирующей RC-цепью.
Установим связь между выходным u2 и входным u1напряжениями, считая входной сигнал u1произвольным.
Используя, второй закон Кирхгофа и соотношения, устанавливающие связь, между напряжениями и токами на элементах схемы, запишем


Подставим полученные напряжения в первое выражение, умножим на RC и продифференцируем один раз по времени
![]()
Если, в этом
соотношение считать, что
![]() .
Последнее означает, что выходной сигнал
есть производная от входного сигнала.
Отсюда и название этой цепи –
дифференцирующая цепь.
.
Последнее означает, что выходной сигнал
есть производная от входного сигнала.
Отсюда и название этой цепи –
дифференцирующая цепь.
Рассмотрим два
частных случая.
А. Пусть входной
сигнал - ступенчатое напряжение амплитудой
Е (рис.6.9)
![]() .
Используя классический метод, определим
отклик цепи.
.
Используя классический метод, определим
отклик цепи.
Составим дифференциальное уравнение и приведем его к стандартному виду:
 .
.
2) Запишем общее решение.
![]() .
.
3) Найдем вынужденную
составляющую общего решения -
![]() .
.
Вынужденную
составляющую находим в стационарном
(установившемся) режиме, который имеет
место когда, t
∞.
В этом случае входной сигнал – пос тоянное
напряжение величины
тоянное
напряжение величины![]() ,
ему соответствует гармонический сигнал
с нулевой частотой
ω=0,т.к.,
,
ему соответствует гармонический сигнал
с нулевой частотой
ω=0,т.к.,![]() =
=![]() cosωt\
(ω=0)
. При таких
условиях наличие индуктивности
равносильно короткому замыканию (ХL=
ωL),
а емкости – разрыву цепи (ХС=
(ωС)-1).
cosωt\
(ω=0)
. При таких
условиях наличие индуктивности
равносильно короткому замыканию (ХL=
ωL),
а емкости – разрыву цепи (ХС=
(ωС)-1).
Для нахождения вынужденной составляющей составим схему замещения исходной цепи при ω=0 (см. рис.6.10а). Из схемы следует, что u2(∞)=0.
4) Найдем показатель экспоненты - р1.
Коэффициенты р находят, как корни характеристического уравнения
RCр1+1=0. Отсюда р 1= - (RC)-1.
5) Найдем произвольную постоянную A1.
Произвольные постоянные находят из начальных условий для искомой функции и ее производных (при t=+0). Значения токов и напряжений в начальный момент времени после коммутации (при t=+0) определяют из схемы замещения исходной цепи, образованной после коммутации, с учетом законов коммутации, по законам Кирхгофа. При нулевых начальных условиях наличие индуктивности равносильно разрыву цепи (iL(-0) = iL(+0)), а емкости - короткому замыканию (uC(-0) = uC(+0)).
Аналогичную схему замещения можно получить, если считать что ступенчатому сигналу в начальный момент времени (t=+0) соответствует гармонический с бесконечно большой частотой (ω∞).
Для дифференцирующей RC-цепи послекоммутационная схема (при t=+0, ω∞) приведена на рис.6.10б, а произвольную постоянную A1 находят из уравнения:
![]() =A1=
=A1=![]() .
.
6) Запись общего решения:
![]() .
.
В ыходное
напряжение представляет собой
экспоненциальный импульс, который
характеризуется двумя параметрами:
ыходное
напряжение представляет собой
экспоненциальный импульс, который
характеризуется двумя параметрами:
Е – амплитуда импульса;
τ - постоянная времени цепи. Определим выходной сигнал при t=τ.
![]()
Отсюда следует, что постоянная времени это время, за которое импульс, убывая по экспоненциальному закон изменяется от Е до уровня 0,37Е (т.е. убывает в е=2,71 раза).
Иногда пользуются третьим параметром. tуст. – время установления выходного напряжения, это время за которое сигнал достигает свое стационарное значение, с заданной точностью от амплитуды импульса. Так время установление на уровне 0,1 и 0,05 составляет tуст.0.1 =2,3τ; tуст.0.05 =3τ.
Б. Пусть входной сигнал одиночный прямоугольный импульс (рис.6.12) амплитудой Е и длительностью tu. Такой импульс представляет собой суперпозицию двух ступенчатых сигналов и записывается как
![]() .
.
Зная отклик на ступенчатый сигнал, и используя принцип суперпозиции можно записать аналитическое выражение для выходного сигнала:
![]()
На рис 6.13 показаны три временных диаграммы выходного сигнала при различных соотношения между τ и tи.

В зависимости от соотношения между τ и tи эта схема имеет три названия.
Если: τ<<tи - то цепь называется дифференцирующей RC-цепью (рис.6.13а).
Если: τ ≈ tи – то цепь называется укорачивающей RC-цепью (рис.6.13б).
Если:τ>> tи - то цепь называется разделительной RC-цепью (рис.6.13в).
Рассмотрим процессы протекающие в цепи при воздействие на вход прямоугольного импульса при нулевых начальных условиях uC(-0)=0.
Напряжения на элементах связаны вторым законом Кирхгофа
u1=uC+uR.
При t<0, u1=0, uC=0, следовательно, uR =0. Это исходное состояние.
При t=+0, u1=Е, uC=0, E=0+ uR. Следовательно, uR=Е. Это послекоммутационное состояние цепи.
П ри
t>0 E= uC+uR.
Происходит заряд конденсатора С током
iзар
заряда, напряжение на нем возрастает,
а на резисторе (на выходе) убывает от Е
к нулю.
ри
t>0 E= uC+uR.
Происходит заряд конденсатора С током
iзар
заряда, напряжение на нем возрастает,
а на резисторе (на выходе) убывает от Е
к нулю.
При t= tи-0, E= uC(tи),+ uR(tи),. К моменту окончания импульса uC= uC(tи), uR=Е- uC(tи).
При t> tи+0 , u1=0=uC+uR.. Следовательно uR = - uC= - uC(tи),. Поэтому знак выходного напряжения меняется на противоположный.
При t> tи, u1=0 , uR = - uC. Происходит разряд конденсатора С током iразр разряда, напряжение на нем убывает, убывает и напряжение на резисторе (на выходе) от - uC(tи) к нулю.
Цепь, состоящая из RL элементов и приведенная на рис 6.14, выполняет аналогичные преобразования над входными сигналами и называется дифференцирующей RL-цепью.
