ЛЕКЦИЯ №16

Сумматоры.

План:

1. Классификация сумматоров.

2. Одноразрядные сумматоры.

3. Многоразрядные сумматоры.

4. Двоично-десятичные сумматоры.

Ключевые слова:

Сумматор, полусумматор, комбинационный сумматор, накапливающий сумматор, последовательный многоразрядный сумматор, параллельный многоразрядный сумматор, двоично-десятичный сумматор, параллельный многоразрядный сумматор с последовательным переносом, параллельный сумматор с параллельным переносом.

Сумматоры являются основой АЛУ и выполняют операцию арифметического сложения слов.

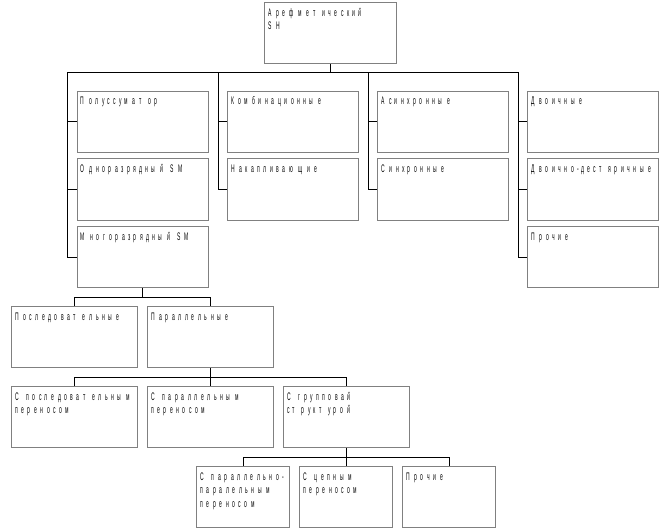
По числу входов различают полусумматоры, одноразрядные и много разрядные сумматоры.

Многоразрядные сумматоры делятся на последовательные и параллельные.

В

последовательных SM на одном и том же сборки обрабатываются поочередно разряд за разрядом, а в параллельных – одновременно по всем разрядам.

По способу ориентации межразрядных переносов параллельных SM подразделяются на схемы с последовательным параллельными переносами и с групповой структурой. В схемах с групповой структурой разрядная сетка разделена на поля, обрабатываемые группами разрядных схем. В группах и ююю ююю могут применяться разные способы переносов, причем в наименовании сумматоров вначале указывается вид переноса ведущий группы.

Комбинационные SM являются комбинационными цепями.

Накапливающие SM имеют память, в которой накапливаются разряды суммирования так, что очередное слагаемое добавляется к результату, содержащемуся в SM.

По способу тактирования различают асинхронные и синхронные SM. В зависимости от системы счисления: 2, 2/10 и прочие.

Полусумматорами – называются устройства с 2-мя входами и 2-мя выходами, по которым вырабатывается ююю суммы и переноса:

Полусумматор реализует лишь часть суммирования, так как не учитывает третьей входной величины – переноса из предыдущего разряда.

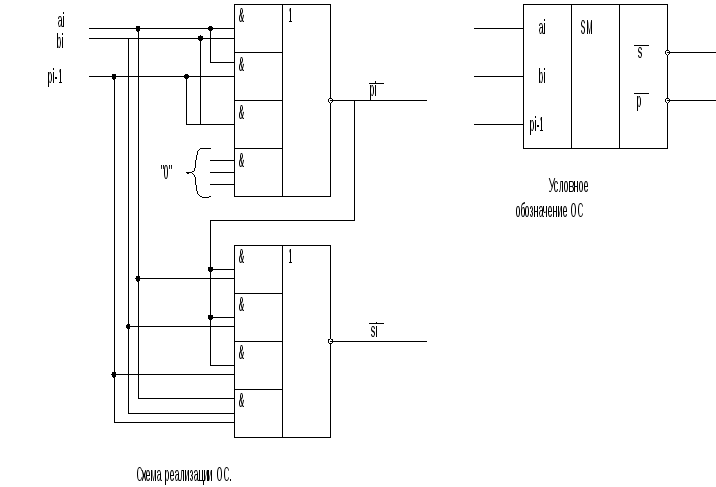
Одноразрядные сумматоры (ОС) имеют 3 входа и обеспечивают сложение с переносом из предыдущего разряда .

Таблица формул ОС:

0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 1 1 0 1 0 0 1	0 0 0 1 0 1 1 1

В таблице объединены строки, имеющие инвертированные аргументы. При этом инвертируются и ююю функций суммы и переноса.

Если X-вектор аргументов, то

Такие функции называются самодвойственными.

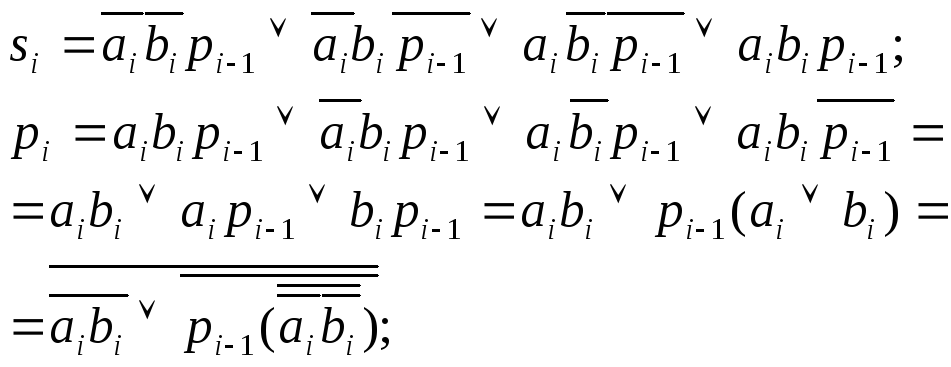
При реализации на элементах ТТЛ сигнал переноса может быть реализован на одном элементе К155ЛР3 (2-2-2-3И-4ИЛИ-НЕ).

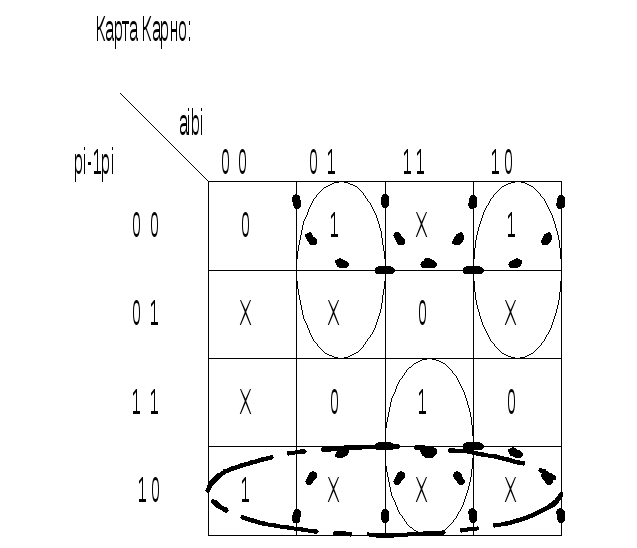
В выражениях для Si необходимо уменьшить число букв в ююю. Это может быть сделано следующим образом:

Составим функцию для Si от 4-х аргументов, используя Pi количество вспомогательных аргументов.

Тогда: При ююю аргументах ставим неопределенные значения.

0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1	0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1	0 x 1 x 1 x x 0 1 x x 0 x 0 x 1

Быстродействующие ОС можно получить при реализации на элементах ЭСЛ.

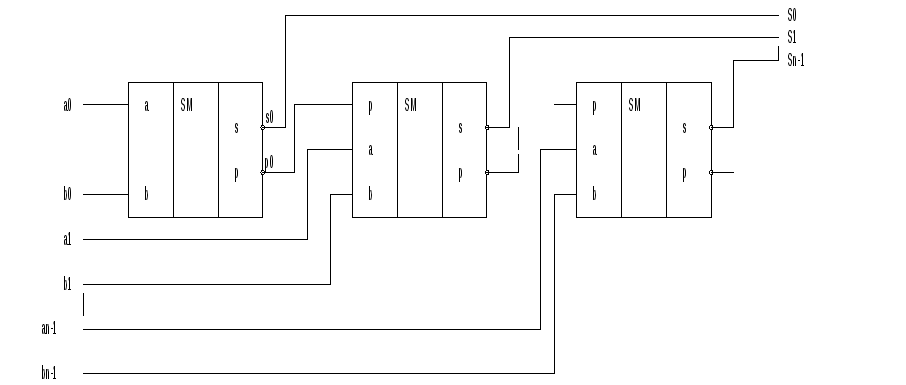
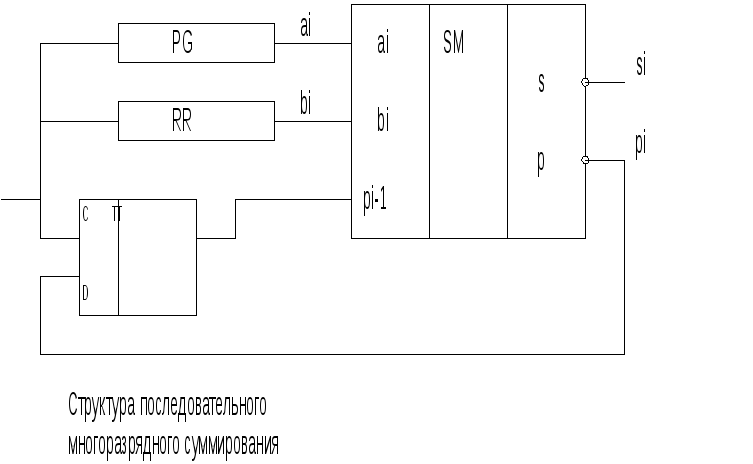
В последовательном многоразрядном SM подача слагаемых начинается с младшего разряда. Получается сумма и перенос в следующий разряд, который задерживается Д - триггером на 1 такт и затем подается на вход SM со слагаемым следующего разряда.

Время выработки суммы:

делитель суммы в ОС.

Параллельные многоразрядные SM. В параллельных многоразрядных SM перенос между разрядами может ююю последовательно, параллельно и комбинированным способом.

Параллельные SM с последовательным переносом применяют ююю параллельно, образуются предварительные разрядные суммы, а после ююю переносов суммы приобретают окончательный вид:

Параллельные SM с параллельным переносом имеют максимальное быстродействие. В каждом разряде одновременно вырабатывается выходные величины.

Такой SM может быть построен как уст. для получения функций суммы и переноса, зависящие только от значений слагаемых независимо от местоположения разряда.

В I (младшем) разряде реализуется функции, зависящие только от слагаемых данного разряда.

Во II разряде функции:

зависят как от слагаемых данного разряда, так и от переноса из предыдущего разряда, который в свою очередь является функцией a0 и b0. Поэтому:

Аналогичным образом в i-том разряде:

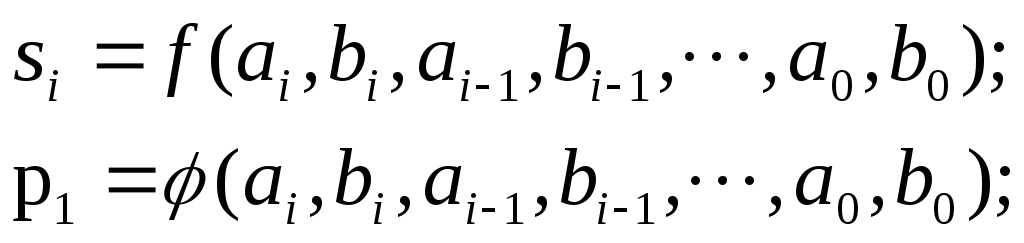
В следующем разряде:

По этим выражениям можно получить значения разрядных сумм во всех разрядах одновременно, так как все аргументы ююю ююю одновременно.

Введем функции генерации и передачи переноса:

Первое слагаемое равно 1, когда возникает перенос в следующий разряд независимо от переноса из предыдущего разряда. Назовем эту функцию генерации:

Выражение в скобках (a_ib_i) определяет условие, при котором перенос на выходе возникает как следствие поступления в данный разряд переноса из предыдущего разряда.

Функция ююю переноса:

Тогда функция переноса из этого разряда в следующий определяется как:

Поэтому обычно различают SM с параллельным переносом только для малого числа разрядов как составные части SM с групповой структурой.

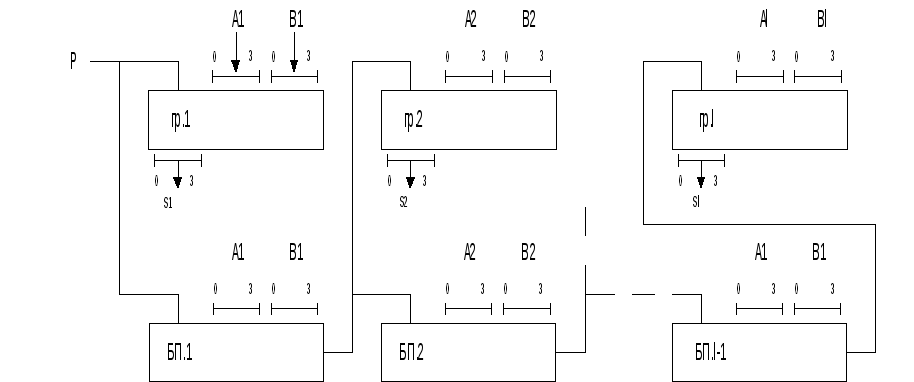
Сумматоры, с групповой структурой имеющие разрядов, состоят из l групп по m разрядов. В группах и между ними возможен различные виды переноса.

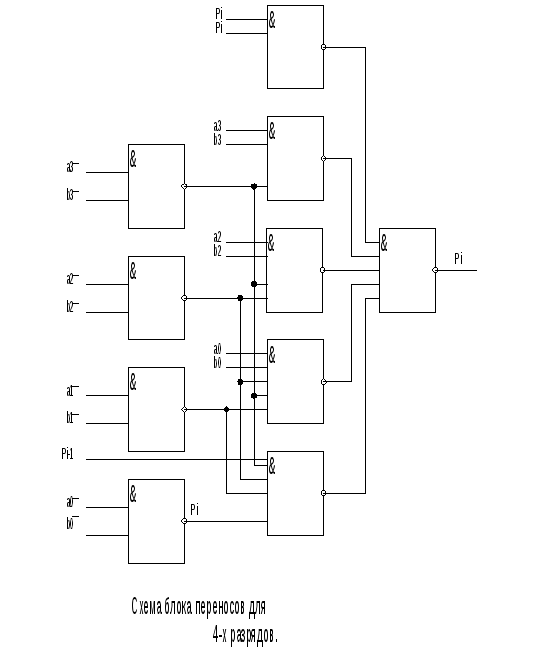
Сумматор с цепным переносом имеет блоки переносов, которые анализируют сложение в пределах группы. Размерность схем переноса уменьшается. Одновременно появляется последовательная передача переноса между группами.

Схема SM с цепным переносом:

Сумматор с параллельно-параллельным переносом имеет параллельный перенос, как в группах, так и между ними, что обеспечивает минимальное время суммирования.

В таком SM дважды повторяется принципиально идентичная организация переносов, причем для сумматора в целом группы являются тем же, что одноразрядные SM для группы. Для группы вырабатываются функции генерации и передачи переносов.

Двоично-десятичные SM выполняют действия над десятичными числами, закодированными двоичными триадами.

Обычный способ построения 2/10 SM предусматривает суммирование тетрад обычным SM и последующею коррекцию результата.

Коррекция нужна, так как при сложении результата может быть >9, тогда как в триаде содержится числа от 0 до 9. Если результат < 9, то коррекция не нужна.

Если при сложении тетрад и переноса из предыдущей тетрады результат находится в пределах 1015, то переноса нет, хотя должен быть перенос в следующею триаду с одновременным уменьшением содержимого на 10. Вычитание 10 заменяется сложением обратного кода 10, т.е. 0110(6). Поэтому к результату надо добавить 6 и сигнал переноса передать в следующею триаду.

Если при сложении сумма превысила 15, появляется сигнал переноса, по ююю этого переноса 16, а должно быть 10. Поэтому также необходимо добавить поправку 6.

В I SM производится сложение тетрад, а во II SM – коррекция результата.

Асинхронные SM имеют перенос время сложения. Этот способ построения SM используется для схем с последовательным переносом и может дать значительный выигрыш во времени в ююю времени сложения. Но на практике не получили широкого распространения так как затруднен обмен информацией между блоками ЭВМ.

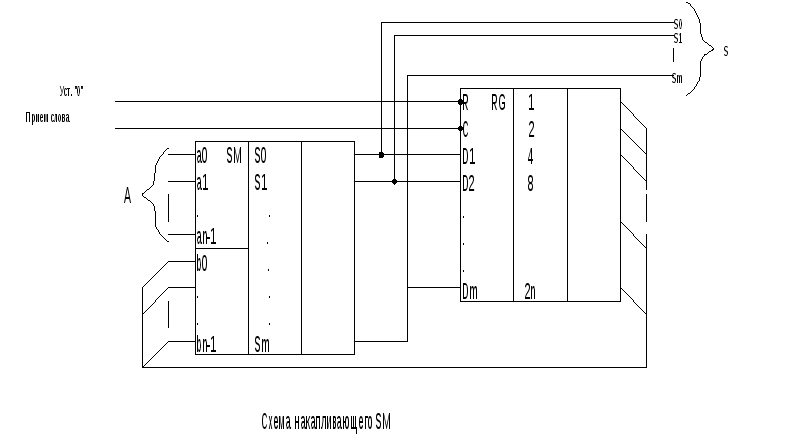
Накапливающие SM реализуются на основе комбинирующих SM и P2.

В комбинационных SM: S:=A+B;

В накапливающих SM: S:=S+A;

Вначале RG устанавливают в нулевое состояние.

Накапливающие SM называются аккумуляторами.

Вопросы для контроля:

1. Как работает мультиплексор?

2. Как можно увеличить размерность мультиплексора?

3. Как различаются входы мультиплексора?

4. Где можно использовать мультиплексоры?

5. Как работает демультиплексор?

Литература:

1. Схемотехника ЭВМ. Учебник для ВУЗов под редакцией Соловьева Г.Н. – М.; Высш.шк., 1985, с.112-120.

2. Угрюмов Е.П. Проектирование элементов и узлов ЭВМ – М.; Высш.шк., 1987, с.157-160.

3. Микропроцессоры т.2/ Под редакцией М.Н.Преснухина – М.; Высш.шк., 1986, с.121-126.

4. «Функциональные узлы цифровой автоматики» Потёмкин И.С. – М.; Энергоатомиздат, 1988г., с.96-102.