ЛЕКЦИЯ №13

Цифровые компараторы.

План:

1. Устройства сравнения на «равенство».

2. Схема сравнения на «больше».

Ключевые слова:

Компараторы, схемы сравнения на «равенство», признак равенства, признак неравенства, схемы сравнения на «больше», многоразрядные схемы сравнения.

Компараторы (устройства сравнения кодов) выполняют микрооперации определяя отношение между 2-мя словами. Основные отношения «=» и «>». Другие отношения могут быть выражены через основные. Так, признак неравенства слов можно получить как отрицание признака равенства , отношение меньше путем перемены местами аргументов в функции:

а нестрогие неравенства:

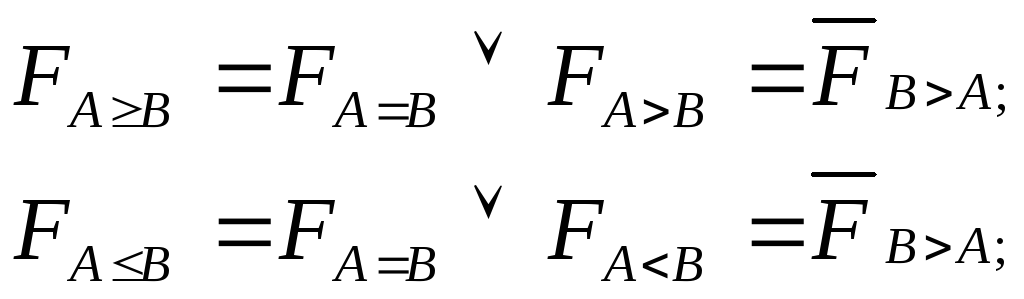
Устройства сравнения на равенство.

Строятся на основе поразрядных операций над одноименными разрядами обоих слов. Признак r равенства разрядов имеет единичное значение, если в обоих разрядах содержаться либо единицы, либо нули, т.е.

В свою очередь признак неравенства разрядов:

В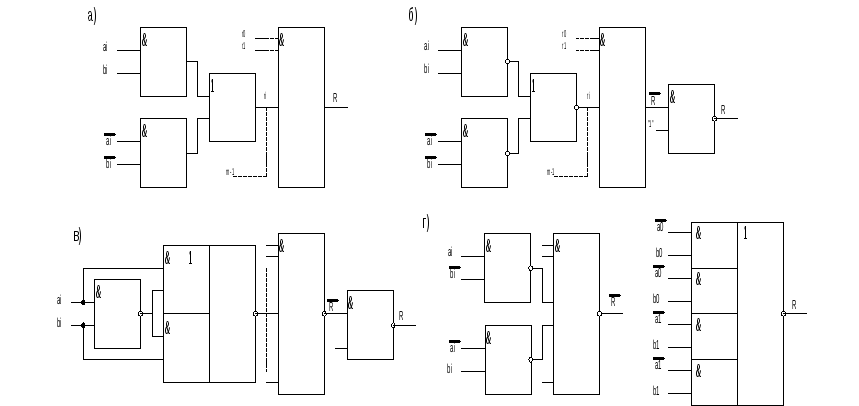 арианты схем сравнения на равенство (сравнения равенства с единичной глубиной):

Признак равенства слов R принимает единичное значение, если все разряды равны, т.е.

Для уменьшения числа внешних выводов целесообразно ююю от парафазных подачи входных переменных. Этого можно достичь как установкой входных инверторов, так и преобразуя формулу, чтобы она не содержала инверсий аргументов.

На основе этого соотношения можно построить схему, в которой число входов сократилось вдвое, а быстродействие не изменилось.

Возможно и 2-х ярусная схема (r), основанная на реализации формулы:

При повышенном быстродействии схема имеет низкую сложность но ее применение ограничено, т.к. для нее нужны элементы с числом входов 2n.

Предельно снизить логическую глубину схемы можно построив схему на элементах И-ИЛИ-НЕ, однако подобная схема пригодна лишь для 2-х разрядных слов в связи с ограниченным числом групп и в промышленных элементах И-ИЛИ-НЕ.

Сравнение на “больше” (меньше).

Для одноразрядных слов функция F_A>B определяется таблицей:

A	B	FA>B
0 0 1 1	0 1 0 1	0 0 1 0

Для 2-разрядных слов: если в старшем разряде a₁=1, b₁=0, то A>B, если a₁=b₁, то следует перейти к анализу младшего разряда, применив те же условия F_A>B=1, если a₁=1, b₁=0.

Таким образом, справедливо соотношение:

где - признак равенства разрядов.

Исходя из этих же соображений можно записать для много - разрядных слов:

т.к. обычно устройство сравнения на «больше» является частью компаратора, в котором происходит также сравнение на равенство, то функция r_i все равно нужны при построении сх. сравнения на > их можно считать готовыми.

Если же рассматривать устройства сравнения на > как самостоятельные, можно получить более простые выражения для функции F_A>B.

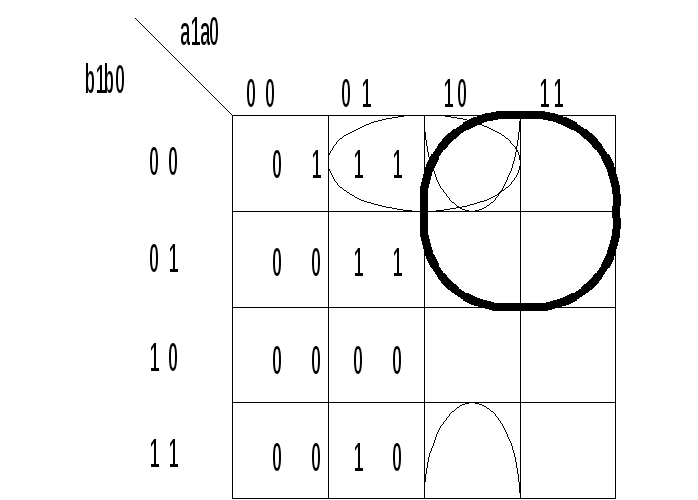
Карта Карно для 2-разрядной функции. (Самостоятельная работа.)

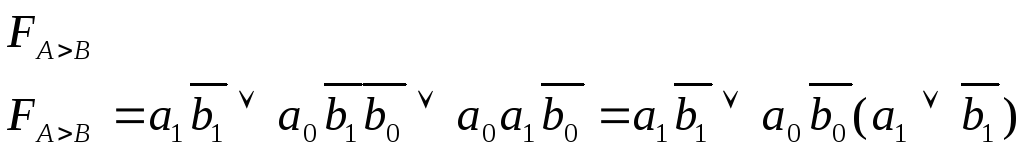
Введем обозначения:

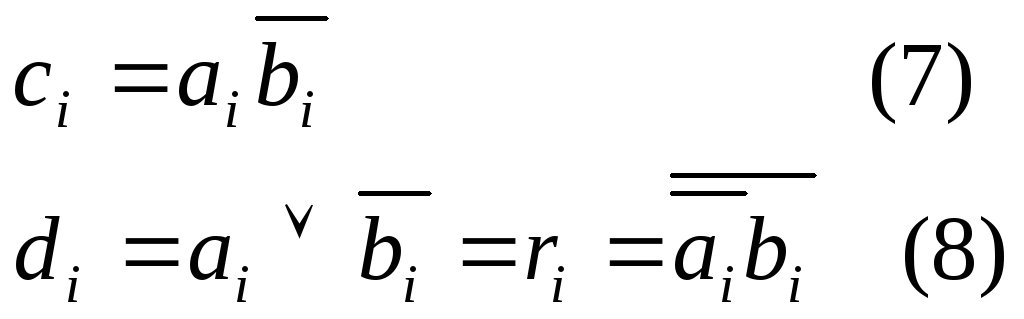
Тогда для много - разрядных слов можно записать:

Схема ююю для 4-х разрядных слов:

Т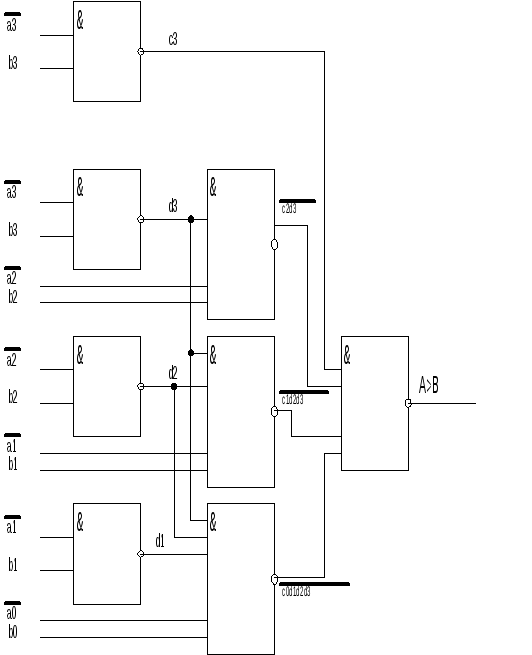 акой компаратор имеет задержку 3t₃ независимо от числа разрядов сравниваемых слов и требует использования элементов с (n+1) входом.

К формуле F_A>B можно применить факторизацию.

Этому представлению ююю схема, в которой применяется однотипные модули c и d и 2-х входные элементы И, ИЛИ. При возрастании разрядности то возникает трудности с числом входов логических элементов, то снижается быстродействие, и для много - разрядных схем она может быть недопустимо большой.

Много - разрядные слова чаще всего сравнивают с помощью групповых структур.

каждая группа представляет собой мало - разрядный компоратор. Выходы компоратора подаются на следующею старшую.

Рассмотрим построение групп на примере 2-х разрядной группы.

Функция F_A>B вырабатывается на основе выражения:

Задержка группы по цепи переноса: t_n=2t₃;

(Самостоятельная работа)

Г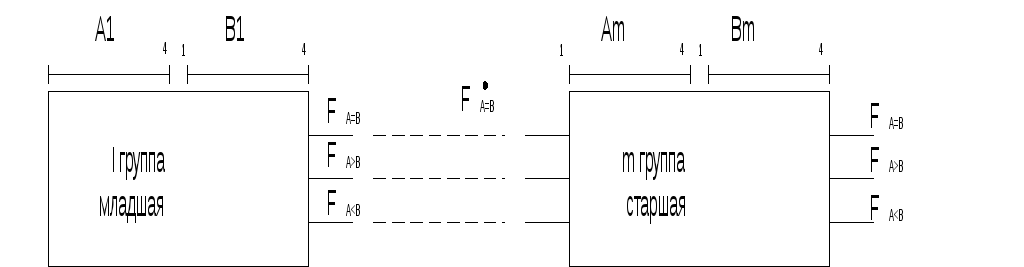 руппы между собой можно соединить последовательно:

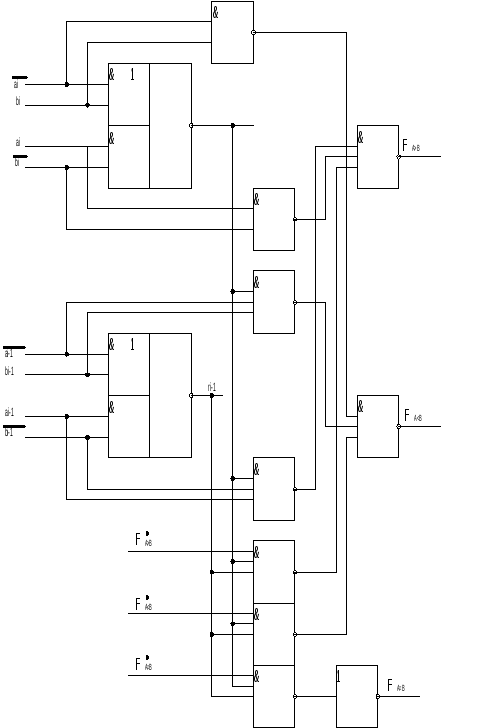
Задержка компаратора в этом случае:

t_k(m-1)t_n+t_гр.;

Компаратор гр. структуры можно построить и иначе, используя функции F_A=B, F_A>B, F_A<B, вырабатываемые в группах, в качестве соот. функций отдельных разрядов внутри группы.

Т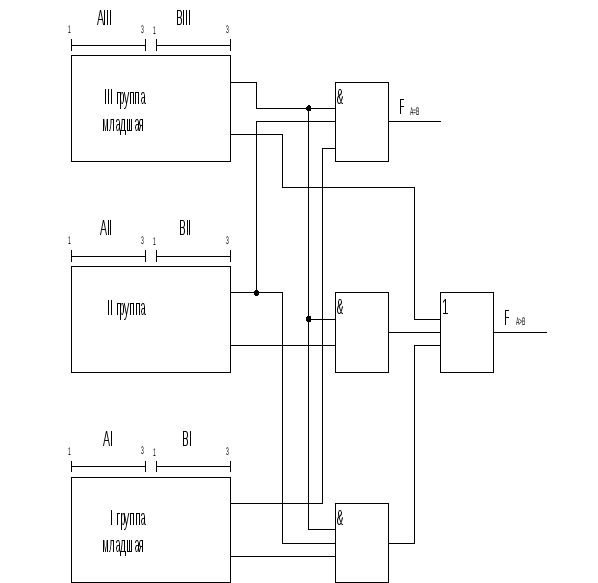 огда получается последовательно-параллельная структура, в которой выходной сигнал определяется для 9-разрядного слова, ююю выражением:

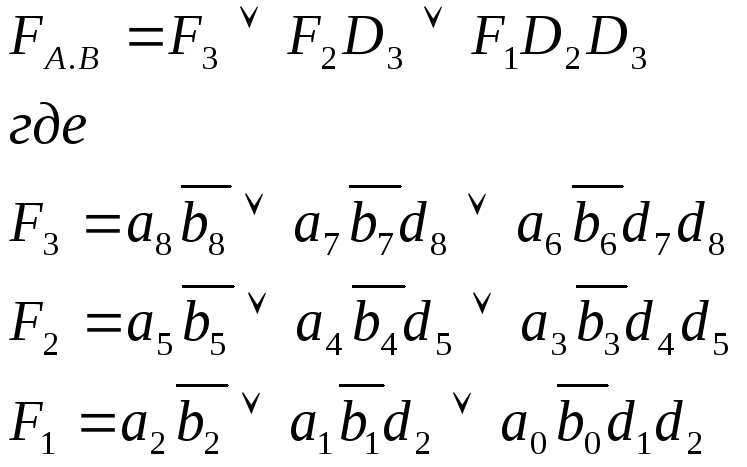
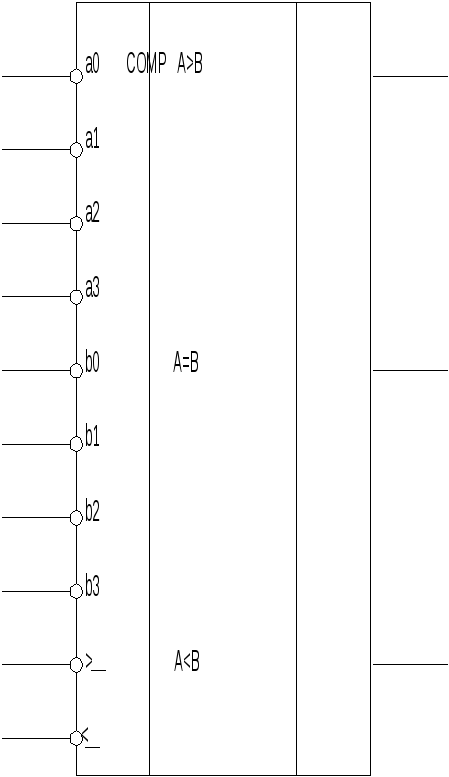
Условное обозначение компаратора.

К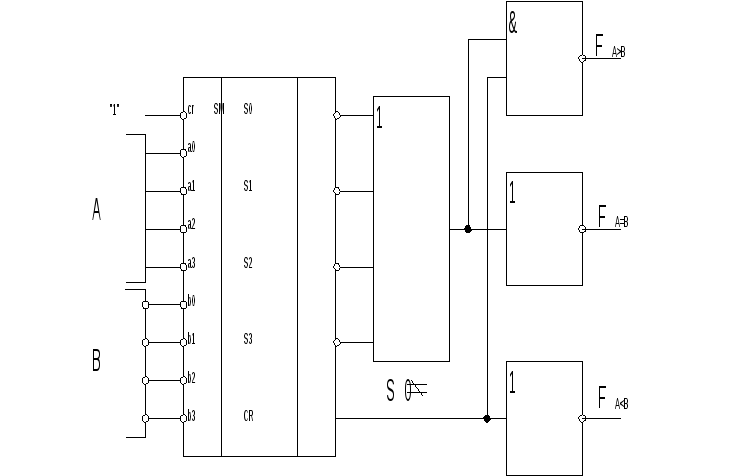 омпаратор можно построить на основе сумматора:

Вопросы для контроля:

1. Как определяется признак равенства двух одноразрядных кодов?

2. Чему равен признак равенства двух многоразрядных кодов?

3. Как выражается признак «больше» для двух одноразрядных слов?

4. Чему равен F_A>B для двух n-разрядных слов?

5. Как выглядит схема сравнения на «больше» для 2-х двухразрядных слов?

Литература:

1. Угрюмов Е.П. Проектирование элементов и узлов ЭВМ – М.; Высш.шк., 1987, с.114-169.

2. «Функциональные узлы цифровой автоматики» Потёмкин И.С. – М.; Энергоатомиздат, 1988г., с.135-139.