
- •1. Основні означення та необхідні відомості з теорії груп та кілець
- •2. Кільця лишків за модулем m
- •3. Кільця поліномів
- •3.1. Поліноми над кільцями
- •3.2. Поліноми над полями
- •3.3. Фактор-кільце f[X]/(f)
- •4. Корені поліномів та їх властивості
- •5. Поля часток
- •Підполя. Прості поля. Характеристики полів
- •Розширення полів
- •Алгебраїчні розширення
- •9. Мінімальні поліноми
- •Прості розширення полів та їх побудова
- •Поля розкладу поліномів
- •12. Теорема про існування та єдиність скінченних полів
- •13. Критерій підполя, діаграми включення підполів
- •14. Мультиплікативна група скінченного поля
- •Наслідки теореми 30.
- •15. Незвідні поліноми та їх корені
- •16. Спряжені елементи
- •17. Зображення елементів скінченних полів
- •18. Порядки поліномів
- •19. Примітивні поліноми
- •20. Сліди та норми
- •21. Базиси
- •22. Автоморфізми скінченних полів
- •23. Зведення основних положень та результатів
- •Предметний покажчик
- •Список використаної літератури
-
Розширення полів
Поле
![]() називається
розширенням
поля
F,
якщо
називається
розширенням
поля
F,
якщо
![]() .
.
Нехай
![]() .
Розглянемо деяку множину елементів
.
Розглянемо деяку множину елементів
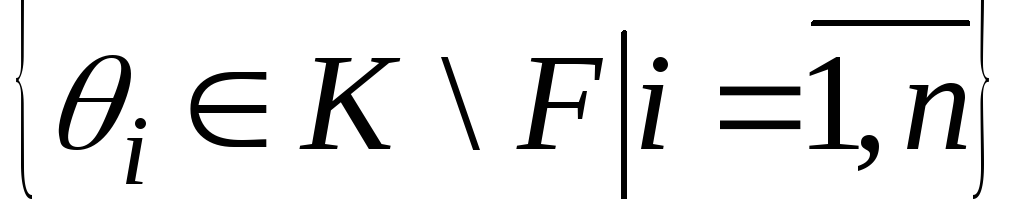 (n
–
не обов'язково скінченне).
(n
–
не обов'язково скінченне).
Найменше
поле, що містить F
і
елементи
![]() ,
називається розширенням
F,
одержаним шляхом приєднання елементів
,
називається розширенням
F,
одержаним шляхом приєднання елементів
![]() ,
і позначається
,
і позначається
![]() .
.
Якщо розширення одержане приєднанням тільки одного елемента, то воно називається простим.
Приклад.
Поле комплексних чисел C є простим розширенням поля дійсних чисел R, яке одержане приєднанням одного елемента – уявної одиниці.
Нехай
F
–
поле. Якщо множина L
є
абелевою
гупою
з операцією додавання, визначена операція
множення елементів
![]() (скалярів) на елементи
(скалярів) на елементи
![]() (вектори), що не виводить за межі
(вектори), що не виводить за межі
![]() ,
і для будь-яких ,
,
і для будь-яких ,
![]() ,
,![]() виконуються
умови:
виконуються
умови:
-
 ;
; -
 ;
; -
 ;
; -
 ,
,
то L називається лінійним векторним простором над F.
ТЕОРЕМА 18. Будь-яке розширення поля F є лінійним векторним простором над F.
Розширення, як і будь-яке поле, є абелевою групою за додаванням. Неважко також бачити, що умови 1) – 4) виконуються.
Система
елементів розширення
![]()
![]() (
(![]() –
скінченна або нескінченна множина
натуральних індексів), для якої виконується
умова
–
скінченна або нескінченна множина
натуральних індексів), для якої виконується
умова
![]() ,
,
![]() ,
називається базисом
,
називається базисом
![]() над
F.
над
F.
Якщо
в розширенні
![]() поля F
існує
базис із скінченною кількістю елементів,
то
поля F
існує
базис із скінченною кількістю елементів,
то
![]() називається
скінченним
розширенням F.
називається
скінченним
розширенням F.
Розмірність
![]() як
лінійного векторного простору над полем
F
називається
степенем
розширення
як
лінійного векторного простору над полем
F
називається
степенем
розширення
![]() і
позначається
і
позначається
![]() .
.
Приклад.
[C
:
R
]=2,
оскільки будь-яке комплексне число а
+ ib
можна
зобразити як двовимірний вектор
(а,b),
![]() R
. Базисом
C
над
R
є
система елементів {1,
i}.
R
. Базисом
C
над
R
є
система елементів {1,
i}.
Будь-яке скінченне поле F є скінченним розширенням свого простого підполя Zp. Його елементи можна представити як вектори деякої розмірності n з компонентами з Zp. Таким чином, справедливе наступне твердження.
ТЕОРЕМА 19. Будь-яке скінченне поле містить рn елементів, де р – деяке просте, а n – натуральне числа. р є характеристикою, а n – степенем розширення поля F над простим підполем Zp.
Скінченні
поля називають полями
Галуа (Galois
Fields)
і позначають
![]() або
або
![]() ,
де рn
– кількість елементів поля.
,
де рn
– кількість елементів поля.
Кількість елементів поля називається його порядком.
Так,
порядок
![]() дорівнює рn.
дорівнює рn.
Тепер
замість Zp
будемо використовувати позначення
![]() .
.
ТЕОРЕМА
20 (про “башту”
розширень).
Нехай
![]() –
скінченне розширення поля
–
скінченне розширення поля
![]() а
а
![]() в свою чергу, – скінченне розширення
поля
в свою чергу, – скінченне розширення
поля
![]() (
(![]() –
так звана «башта» розширень ). Тоді
–
так звана «башта» розширень ). Тоді
![]() .
.
Нехай
![]() ,
,![]() .
У
.
У
![]() як
лінійному векторному просторі над F
існує
базис
як
лінійному векторному просторі над F
існує
базис
![]() ,
а в L
над
,
а в L
над
![]() –
базис
–
базис
![]() .
Одержуємо:
.
Одержуємо:![]() ,
де
,
де
![]() .
Доведемо, що
.
Доведемо, що
![]() – базис в L
над
F,
що містить mn
елементів,
тобто
– базис в L
над
F,
що містить mn
елементів,
тобто
![]() :
:
![]() .
.
Отже,
![]() – базис L
як
лінійного векторного простору над F.
Таким чином,
– базис L
як
лінійного векторного простору над F.
Таким чином,
![]()
![]() .
.
-
Алгебраїчні розширення
Елемент
![]() називається алгебраїчним
над
F,
якщо він є коренем деякого полінома з
називається алгебраїчним
над
F,
якщо він є коренем деякого полінома з
![]() .
.
Приклад.
Уявна
одиниця i
![]() C
є
алгебраїчним над R
елементом,
оскільки є коренем полінома х2+1
C
є
алгебраїчним над R
елементом,
оскільки є коренем полінома х2+1![]() R
[x].
Цей корінь не лежить в R,
але лежить в його розширенні C
.
R
[x].
Цей корінь не лежить в R,
але лежить в його розширенні C
.
Розширення поля F називається алгебраїчним над F, якщо всі його елементи – алгебраїчні над F.
ТЕОРЕМА
21.
Кожне
скінченне розширення
![]() поля
F
є
алгебраїчним над F.
поля
F
є
алгебраїчним над F.
Нехай
![]() ,
θ
–
довільний
елемент
,
θ
–
довільний
елемент
![]() .
Система елементів 1,
θ
,
.
Система елементів 1,
θ
,![]() ,
як і кожна система з n+1
елемента,
повинна
бути лінійно залежною. За визначенням
лінійної залежності
існує ненульовий набір коефіцієнтів
,
як і кожна система з n+1
елемента,
повинна
бути лінійно залежною. За визначенням
лінійної залежності
існує ненульовий набір коефіцієнтів
![]() таких,
що
таких,
що
![]() .
А це і означає, що
є коренем деякого полінома над F.
.
А це і означає, що
є коренем деякого полінома над F.
Контрольні питання до §7,8
-
Дати визначення розширення поля, підполя.
-
Дати визначення алгебраїчного розширення поля,
-
Сформулювати теорему про кількість елементів поля.
-
Сформулювати теорему про башту розширень.
-
Як пов’язані скінченність розширення та його алгебраїчність?
Задачі до §7,8
-
Нехай F розширення К,
 - алгебраїчний над К.
Довести: К(Θ)
– скінченне розширення К.
- алгебраїчний над К.
Довести: К(Θ)
– скінченне розширення К. -
* Довести, що розширення поля, отримані приєднанням до цього поля двох різних коренів незвідного поліному, ізоморфні.
-
Побудувати таблиці операцій для поля F3(Θ), де Θ – корінь поліному
 .
Довести, що 2(Θ)+2
також є коренем цього поліному.
.
Довести, що 2(Θ)+2
також є коренем цього поліному. -
*Нехай L – деяке розширення поля К. Довести: L – скінченне L=K(Θ1, Θn), де Θi - алгебраїчні над К, тобто L отримане з К приєднанням скінченної кількості алгебраїчних над К элементів.
-
* Нехай Θ – алгебраїчний над L, L – алгебраїчне розширення К. Довести: Θ – алгебраїчний над К. Іншими словами: якщо F – алгебраїчне розширення L, L – алгебраїчне розширення К, то F – алгебраїчне розширення К.
-
Нехай L – розширення К, [L:K]=p – просте число. Довести: якщо
 ,
то
,
то
 або F=L.
або F=L.
