Л.О. Завадська

ПРИКЛАДНА АЛГЕБРА:

скінченні поля

Навчальний посібник

КИЇВ – 2010

УДК	519.2
ББК	22.172 (4Укр)
	К 56

ЗМІСТ

1. ОСНОВНІ ОЗНАЧЕННЯ ТА НЕОБХІДНІ ВІДОМОСТІ З ТЕОРІЇ ГРУП ТА КІЛЕЦЬ..........................................................................................4

2. КІЛЬЦЯ ЛИШКІВ ЗА МОДУЛЕМ ...........................................................8

3. КІЛЬЦЯ ПОЛІНОМІВ..................................................................................10

3.1. Поліноми над кільцями....................................................................10

3.2. Поліноми над полями ......................................................................13

3.3. Фактор-кільця ...................................................................14

4. КОРЕНІ ПОЛІНОМІВ ТА ЇХ ВЛАСТИВОСТІ..........................................16

5. ПОЛЯ ЧАСТОК.............................................................................................17

6. ПІДПОЛЯ. ПРОСТІ ПОЛЯ. ХАРАКТЕРИСТИКИ ПОЛІВ......................19

7. РОЗШИРЕННЯ ПОЛІВ................................................................................21

8. АЛГЕБРАЇЧНІ РОЗШИРЕННЯ...................................................................23

9. МІНІМАЛЬНІ ПОЛІНОМИ.........................................................................23

10. ПРОСТІ РОЗШИРЕННЯ ПОЛІВ ТА ЇХ ПОБУДОВА............................25

11. ПОЛЯ РОЗКЛАДУ ПОЛІНОМІВ..............................................................27

12. ТЕОРЕМА ПРО ІСНУВАННЯ ТА ЄДИНІСТЬ СКІНЧЕННИХ ПОЛІВ..........................................................................................................27

13. КРИТЕРІЙ ПІДПОЛЯ, ДІАГРАМИ ВКЛЮЧЕННЯ ПІДПОЛІВ...........29

14. МУЛЬТИПЛІКАТИВНА ГРУПА СКІНЧЕННОГО ПОЛЯ....................30

15. НЕЗВІДНІ ПОЛІНОМИ ТА ЇХ КОРЕНІ...................................................32

16. СПРЯЖЕНІ ЕЛЕМЕНТИ............................................................................34

17. ЗОБРАЖЕННЯ ЕЛЕМЕНТІВ СКІНЧЕННИХ ПОЛІВ............................35

18. ПОРЯДКИ ПОЛІНОМІВ............................................................................38

19. ПРИМІТИВНІ ПОЛІНОМИ.......................................................................42

20. СЛІДИ ТА НОРМИ.....................................................................................43

21. БАЗИСИ.......................................................................................................46

22. АВТОМОРФІЗМИ СКІНЧЕННИХ ПОЛІВ..............................................48

23. ЗВЕДЕННЯ ОСНОВНИХ ПОЛОЖЕНЬ ТА РЕЗУЛЬТАТІВ.................50

ПРЕДМЕТНИЙ ПОКАЖЧИК..........................................................................53

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ...................................................55

1. Основні означення та необхідні відомості з теорії груп та кілець

Означення відмічатимемо знаком , початок і кінець доведення – відповідно значками та , а зауваження – знаком  .

 Нехай – довільна множина, – множина впорядкованих пар . Відображення будемо називати (бінарною) операцією на .

Таким чином, кожній парі ставиться у відповідність елемент – результат операції: (операцію позначили через ). Те, що належить множині , означає замкненість множини відносно операції .

 Під алгебраїчною структурою будемо розуміти деяку множину з однією або кількома операціями на ній. Саму множину називають при цьому носієм даної алгебраїчної структури.

 Напівгрупою називається алгебраїчна структура з однією операцією , що задовольняє умові асоціативності:

.

 Групою називається алгебраїчна структура з однією операцією , для якої виконуються умови:

1. операція асоціативна;

2. існує елемент такий, що для будь-якого

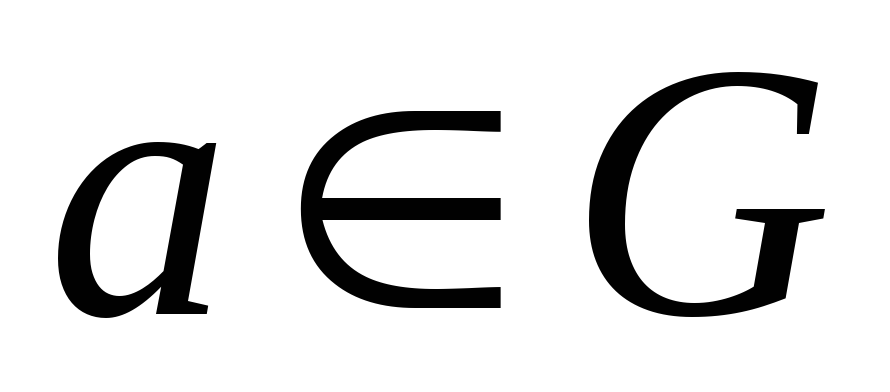
( ‑ одиничний або нейтральний елемент);

3. для будь-якого існує елемент такий, що

(– обернений до елемент).

 Група називається скінченною (відповідно нескінченною), якщо кількість її елементів скінченна (відповідно нескінченна). Кількість елементів скінченної групи називається її порядком.

 Якщо операція в групі комутативна:

(,

то група називається абелевою.

 Групову операцію можна трактувати як множення, тоді говорять про мультиплікативний запис операції або мультиплікативну групу. Якщо ж операція в групі розуміється як додавання, то групу називають адитивною.

 Мультиплікативна група назиавється циклічною, якщо в ній існує такий елемент що ціле таке, що , тобто кожен елемент групи є степенем деякого елемента Елемент називається твірним елементом групи, а циклічну групу позначають .

У разі адитивного запису групової операції має місце те саме означення з заміною степеня на кратне .

 Підмножина групи називається підгрупою , якщо сама утворює групу відносно операції групи .

ТЕОРЕМА (Лагранжа) Порядок підгрупи скінченної групи ділить порядок .

 Відображення групи у групу називається гомоморфізмом групи у , якщо воно зберігає операцію групи . Тобто, якщо та ‑ операції відповідно у групах та , то . Якщо, крім того, відображення “на”, то називається епіморфізмом (або гомоморфізмом “на”). Гомоморфізм у називається ендоморфізмом цієї групи. Якщо взаємно-однозначний гомоморфізм групи на групу , то він називається ізоморфізмом, і в такому випадку говорять, що групи та ізоморфні. Ізоморфізм групи на називається автоморфізмом цієї групи.

 Кільцем називається алгебраїчна структура з двома операціями, які умовно назвемо додаванням та множенням. При цьому:

1. відносно операції додавання утворює абелеву групу;

(нейтральний елемент цієї групи позначається , обернений до ‑ через , він називається протилежним до елементом);

2. відносно операції множення утворює напівгрупу;

3. операції додавання та множення пов’язані законами дистрибутивності:

u Якщо в кільці існує нейтральний елемент за множенням, то називається кільцем з одиницею.

u Якщо операція множення в кільці комутативна, то називається комутативним кільцем.

u Якщо в комутативному кільці з одиницею немає дільників нуля, тобто або , то називається областю цілісності або цілісним кільцем.

В області цілісності можна скорочувати на елементи, відмінні від 0: .

 Область цілісності називається евклідовим кільцем, якщо існує таке відображення множини ненульових елементів у множину невід’ємних цілих чисел, що для будь-яких , існують елементи такі, що причому або . Іншими словами, в можливе ділення з лишком.

Прикладом комутативного кільця з одиницею є множина цілих чисел із звичайними операціями додавання та множення. Це кільце є цілісним, більше того, це евклідове кільце (достатньо визначити як абсолютну величину числа ).

 Підмножина кільця називається підкільцем, якщо замкнене відносно операцій кільця і утворює кільце відносно цих операцій.

 Надалі в цьому параграфі під будемо розуміти комутативне кільце з одиницею.

 Підкільце кільця називається ідеалом цього кільця, якщо (підкільце “витримує” множення на всі елементи кільця ).

 Ідеал кільця називається головним, якщо існує елемент такий, що , тобто складається з елементів, кратних . Кажуть, що головний ідеал породжується елементом і позначають .

 Цілісне кільце, в якому кожен ідеал є гловним, називається кільцем головних ідеалів.

Наприклад, кільце цілих чисел є кільцем головних ідеалів. Кожен ідеал у ньому складається з чисел, кратних деякому цілому числу , тобто . Так, парні числа утворюють ідеал (2).

Кожен ідеал кільця визначає розбиття на класи лишків за модулем ідеалу . Клас лишків, що містить елемент , позначатимемо ; він складається з усіх елементів виду . Два елементи належать одному класу лишків тоді і тільки тоді, коли .

Множина класів лишків кільця за модулем ідеалу утворює кільце відносно операцій додавання та множення, що визначені наступним чином:

або, що те саме,

Кільце класів лишків кільця за модулем ідеалу з операціями, визначеними вище, називається фактор-кільцем кільця за ідеалом і позначається

 Оборотним елементом кільця називається такий елемент , для якого виконується умова ):. Елемент називається оберненим до і позначається .

Нуль кільця є необоротним елементом.

Поняття гомоморфізму природним чином поширюється і на кільця.

 Відображення кільця у кільце називається гоморфізмом, якщо та .

Таким чином, гомоморфізм зберігає обидві операції кільця та індукує гомоморфізм адитивної групи кільця в адитивну групу кільця .

Так само поширюються на кільця поняття епі-, ендо-, ізо- та автоморфізмів.

 Множина називається ядром гомоморфізму .

ТЕОРЕМА (про гоморфізм кілець)*) Якщо гоморфізм кільця на кільце , то ідеал кільця і ізоморфне фактор-кільцю Навпаки, якщо ідеал кільця , то відображення , що визначається умовою : , є гомоморфізмом кільця на з ядром .

 Полем називається алгебраїчна структура з двома операціями: додаванням і множенням, що задовольняють умовам:

1. за додаванням є абелевою групою;

2. за множенням усі ненульові елементи також утворюють абелеву групу;

3. додавання і множення пов'язані законом дистрибутивності:

.

З означення поля видно, що на відміну від комутативного кільця з одиницею, у полі кожен ненульовий елемент є оборотним.

 Надалі приймемо позначення: N – множина натуральних чисел, Z – кільце цілих чисел, Q – поле раціональних чисел, R – поле дійсних чисел, C – поле комплексних чисел.

_____________________

*) Ця теорема, а також поняття ядра гомоморфізму та фактор-кільця є узагальненням відповідних понять та теореми теорії груп.

Контрольні питання до §1

1. Дати визначення групи, кільця, поля та навести приклади цих алгебраїчних структур.

2. Сформулювати теорему Лагранжа.

3. Дати визначення порядку елемента групи.

4. Дати визначення гомоморфізму груп та кілець.

5. Сформулювати теорему про гомоморфізм кілець.

Задачі до §1.

1. Чи буде групою:

- множина натуральних чисел (з нулем) відносно операції додавання;

- множина натуральних чисел (без нуля) відносно операції множення;

- множина цілих чисел відносно операції додавання;

- множина цілих чисел відносно операції множення;

- множина дійсних чисел відносно операції додавання;

- множина дійсних чисел відносно операції множення;

- множина дійсних чисел без нуля відносно операції множення?

2.^* Довести, що у скінченному кільці елемент є оборотним тоді і тільки тоді, коли він нє дільником 0.

Розглянути два випадки: коли кільце комутативне и некомутативне.

3. Побудувати таблицю Келі для групи перестановок S₃. За таблицею знайти:

- всі підгрупи та класи суміжності за ними;

- порядки всіх елементів в групі.