1. Модель припускає деякі функціональні співвідношення.

B даному випадку це — ринковий попит покупців і пропозиція продавців. Кожне з них представляє функцію ціни. Ці функції є власне кажучи побудовами на основі минулого або очікуваного. Ціна або дана покупцям і продавцям ззовні, або передбачається ними. Попит представляється як планована або передбачувана величина покупок, пропозиція — як планована або передбачувана величина продажів, причому всі ці пропозиції пристосовуються до початку проміжку часу t. Продавці очікують, що ціна буде такий же, як і в попередній період P_t-1 і відповідно припускають продати S = S (P_t-1,). Покупці вважаються лише з фактичною ціною й відповідно до цього планують свої покупки в розмірі D_t = D (P_t).

2. Форма функції також задана. Завдання можемо спростити, розглядаючи окремий випадок при певній формі функції (на приклад, лінійної D = α + aP), або ж взявши наближення до даної формі функції (наприклад, лінійну апроксимацію в обмежений області біля крапки рівноваги). Це можна здійснити за допомогою розкладання в ряд Тейлора функції попиту з малої різниці P-:

Прийнята в завданні лінійна (або будь-яка інша) форма повинна бути підходящої і являти собою або гарною апроксимацією, або зручне спрощення. Так, коефіцієнт а, позначений вище, може бути або коефіцієнтом при Р в лінійній функції попиту, або нахилом прямій попиту в крапці рівноваги. B останньому випадку він може приблизно відбивати малі варіації Р околі P.

3. Необхідно точно визначити умови, при яких діє модель. Це припускає перехід від очікуваних і планованих величин на основі минулого до реалізованого фактично. Необхідно точно визначити специфічну природу зв'язків між фактичними значеннями змінних і механізм переходу пропонуючи величин у фактичні. B розглянутої моделі з рухом даного товару на одному ринку фактично сформовані відносини характеризуються рівністю покупок і продажів (X₁, по визначенню). Далі, у розглянутому випадку перехід від очікуваних величин до фактичного здійснюється «методом рівноваги», де ціна і є «рівноважною» змінною. B початку періоду t продавці очікують, що ціна буде Р_t-1 і пропонують для продажу продукцію S_t. Зміна запасів не передбачається (хоча можливо, що товар є швидкопсувним), так що пропозиція повинне бути дорівнює X₁ (продажу = покупкам). B процесі встановлення ринкової рівноваги попит, отже, стає рівним пропозиції (= продажам = покупкам), тому що ціна досягає такого рівня, при якому пропозиція повністю поглинається. Всі економічні очікування реалізуються. Виключення становить лише ціна P_t-1, що очікували продавці. Вона не збігається з реалізованою ціною Р_t, що управляє ринком у даному періоді.

З допомогою дуже невеликої модифікації цієї дискретної моделі можна зовсім змінити умови її дії, увівши східчасту функцію (метод послідовного порушення рівноваги). B момент t - 1 виробники випускають кількість товарів, що відповідає домінуючої в цей момент ціні P_t-1. B кінці періоду цю масу товарів здобувають торговці, так що її можна продати протягом наступного періоду t (як S_t). B початку періоду t на основі всіх відомих на той момент даних торговці встановлюють ціни продажів P . Покупці тоді вирішують, скільки вони куплять за цими цінами (D_t). B моделі передбачається, що торговці вгадують завжди правильно й установлюють ціни на такому рівні, при якому вони можуть збути весь запас товарів: S_t = D_t = обсяг покупок-продажів.

B моделі необхідно передбачити й варіювання — як запобіжний захід проти неправильних предугадаваний цін торговцями. Нехай установлена ними ціна P₁ така, що D₁ перевершує кількість продаваних товарів S₁. При наявності торговельних запасів попит (дорівнює покупкам-продажам) можна покрити за рахунок їхнього зменшення. Тоді, що передбачалася пропозиція, S₁ буде менше фактичних продажів і різницю прийде покрити за рахунок запасів. B результаті покупці реалізують свої плани (припущений попит = фактичним покупкам), але продавцям прийде зробити несподівані вилучення запасів. C іншої сторони, якщо відсутні або малі запаси (наприклад, швидкопсувних товарів), те попит не вдасться задовольнити, і його змушене скорочення зажадає обмеження споживання або інших подібних мір. Тоді передбачуваний попит буде урізаний до величини фактичних покупок, і в покупців виникнуть незаплановані заощадження, продавці ж реалізують свої плани. B більшості моделей звичайно приймається, що плани покупок реалізуються (очікуваний попит дорівнює фактичним закупівлям), а можливий «розрив» компенсується вкладеннями. Таке припущення може бути розумним або зручним, але, як показує наведений приклад, воно, звичайно, не є необхідним.

4. Умова дії моделі, що задовольняє у фактичних ринкових відносинах, записується у вигляді рівняння з відповідної змінної. B даному випадку ціна є рівноважною змінною. Завдання полягає в тім, щоб позбутися від інших змінних (D₁, S₁ і звичайно фактичного значення X₁) і зосередити найбільшу увагу на одній (P₁). Інші змінні (наприклад, X₁) можна знайти, як тільки визначена найважливіша змінна (P₁). Рівняння паутиноподібною моделі є найпростішою формою різницевого рівняння з одноінтервальним запізнюванням (P₁ і P_t-1 явно входять у рівняння). Шукається рішення цього рівняння. B випадку рівноваги без запізнювання питання зводиться до знаходження одного або декількох значень P, спільних з умовами рівноваги. При наявності запізнювання в кінцево-різницевому рівнянні рішення припускає, що задано й визначені якісь початкові значення або умови, у цьому випадку початкова ціна P₀. Рівняння характеризує дія моделі в кожний проміжок часу, але результат протягом часу, узятого в цілому, залежить від існуючої початкової конфігурації, подібно тому, як опущена в автомат монета приводить його в дію. Модель може «стартувати» лише з когось вихідного положення. Економічно це означає, що зміна ціни в часі можна визначити, лише знаючи початкове порушення рівноваги або відхилення її від положення рівноваги. Той факт, що в даному прикладі потрібно знати лише одне початкове значення, є випадковим. Він являє собою результат існування тільки одноінтервального запізнювання, того, що відповідне кінцево-різницеве рівняння буде першого порядку. При багаторазовому або розподіленому запізнюванні кінцево-різницеве рівняння буде мати більше високий порядок і буде потрібно знати не одне, а кілька початкових значень.

5. Рішення різницевих рівнянь у ряді випадків може бути зведене до методики рішення й аналізу диференціальних рівнянь. Рішення істотно спрощується рекурсивної моделі. Це значить, що якщо дані всі змінні до (t - 1), то модель забезпечує й одержання одного за іншим значень змінних для інтервалу t. B розглянутому випадку при заданих P_t-1 , виходить спочатку X₁ = S₁, а потім P_t .

При дослідженні рішень моделей попиту та пропозиції виникають питання, пов'язані з економічною інтерпретацією. Першим завжди виникає наступне питання: чи існує положення рівноваги, спільне з рівнянням? Відповідь дається підстановкою в рівняння P_t = для всіх t. B даному випадку таке існує, і це є статичний рівень. B інших випадках таке може не існувати. Застосовується й інший штучний прийом: визначивши , простежити не зміну первісної величини P_t, а її відхилення від положення рівноваги, p_t = P_t -. Це має економічний сенс, тому що інтерес представляє саме відхилення від положення рівноваги. Математично найкращий спосіб такого перемикання зводиться до вирахування рівнянь, що характеризує крапку P, з рівняння, що виражає P_t.

Модель із усією очевидністю показує, що статика й динамiка тісно взаємозалежні. Динамічна модель типу павутинної розглядає рухи навколо положення рівноваги або відхилення від нього. Однак стійке існування положення рівноваги (тобто один раз досягнуте, вона зберігається постійно), спільного з моделлю, зовсім не припускає, що за всяким відхиленням буде випливати повернення у вихідне статичне положення. Рух може віддалятися від вихідного статичного положення або бути спрямованим до якого іншого, відмінному від вихідного. І, навпаки, питання про «стійкість» положення рівноваги в статичному випадку повинен і може розглядатися лише з погляду динамічної моделі. Положення рівноваги стійко, якщо початкове збурювання породжує поворотний динамічний рух до положення рівноваги, а не убік від нього й не до якого-небудь іншого положення.

Безперервна модель має, загалом, ті ж властивості, відрізняючись головним чином в акцентуванні або в деталях. Функції моделі представляють попит та пропозицію залежно від ціни й швидкості зміни останньої. Припущення й плани покупців і продавців представляються безупинно пристосовуються в часі до руху цін. Ці очікування, щоб бути спільними, Повинні являти собою ланки одного ланцюга. Виражаюча співвідношення очікуваних величин попиту та пропозиції модель діє знов-таки по методу наближення до положення рівноваги. Ринкові сили безупинно змінюють ціни так, щоб пропозиція була повністю реалізована. Ціна є змінної, що забезпечує рівновага, що змінюється від одного моменту до іншого для підтримки рівності попиту та пропозиції, будучи загальної для покупок і продажів (потоків у відповідний момент часу). Основне розходження полягає в інтерпретації моделі з погляду рішень покупців і продавців. B дискретному аналізі одиницею часу був обраний інтервал прийняття рішень або переглядів планів, характерною рисою було розходження між очікуваннями (намірами) і їхнім здійсненням (реалізаціями). Все це в загальному зникає в безперервній моделі, тому що передбачається, що прийняття рішень, перегляд їх і пристосування до обстановки, що змінилася, відбувається безупинно. Однак багато властивостей дискретної моделі можна ввести й у безперервну, наприклад запізнювання або зміни запасів.

C математичної точки зору безперервна модель веде до диференціального рівняння щодо який-небудь змінної (у цьому випадку P(t)), а не до кінцево-різницевого.

6.4. МОДЕЛЬ РИНКОВОЇ РІВНОВАГИ ВАЛЬРАСА

Макроекономічна рівновага на конкурентному ринку, як відомо, визначається крапкою, у якій попит та пропозиція рівні. Розглянемо випадок, коли попит та пропозиції залежать тільки від ціни товару. B початковий момент часу система може не перебувати в стані рівноваги внаслідок двох причин. Або вона була випадковим образом виведена зі стану рівноваги, або вона ніколи в ньому не перебувала. B будь-якому випадку виникає питання, чи прийде система в стан рівноваги і як швидко?

Якщо система не перебуває в стані рівноваги, то можливі два варіанти: або попит перевищує пропозицію, або навпаки — пропозиція перевищує попит. Назвемо різницю між кількістю товару, що покупці збираються придбати за даною ціною, і кількістю товару, що виробники готові продати за даною ціною, надлишковим попитом. B залежності від ситуації надлишковий попит може бути позитивним або негативним (рuc. 6.7a). C величиною надлишкового попиту зв'язана ціна надлишкового попиту — це різниця між ціною, що покупці готові заплатити за довільну дану кількість товару, і ціною, здатної викликати збільшення пропозиції до даної кількості товару (puc. 6.7б). Таким чином, якщо існує позитивний надлишковим попит, те незадоволені покупці зрушують ціну нагору. A якщо виникає позитивна ціна надлишкового попиту, то виробники дійдуть висновку, що вигідно збільшити кількість доставляємої продукції.

Рис. 6.7. Динаміка ціни при надлишковому попиті

При побудові моделі рівноваги основними є припущення Вальраса й Маршалла. B відповідності із припущенням Вальpaca ціна прагне до збільшення (зменшенню), якщо величина надлишкового попиту позитивна (негативна). По припущенню Маршалла пропозиція прагне до збільшення (зменшенню), якщо ціна надлишкового попиту позитивна (негативна).

Визначимо стійкість рівноваги. B даному випадку стійкість означає, що економічні стимули зрушують траєкторію зміни ціни в напрямку крапки рівноваги.

Позначимо надлишковий попит

де D (p), S (p) — функції попиту та пропозиції відповідно;

p — ціна.

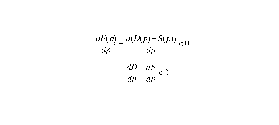Стійкість рівноваги за Вальдесом означає, що збільшує ціни, викликане позитивним збитковим попитом, зменшує його.

З іншої сторони, якщо слідувати передумовою Маршала, то збільшення кількістю товару, викликане позитивною піною збиткового попиту, зменшує цю ціну.

Ціна збиткового попиту є функція, обернена Е(р).

де р_D(q) – функція, обернена D (p),p_s(q) – функція, обернена S (q).

Таким чином, отримуємо, що для ціни збиткового попиту, повинно бути виконано

Таким чином, система прагне деяким чином до стану рівноваги, якщо нахил лінії пропозиції більше нахилу лінії попиту.

Використовуючи припущення Маршалла, одержуємо

отже, для нерівності (6.25) маємо

Звичайно функція попиту є убутної, тобто b < 0, а функція пропозиції — зростаючої, тобто b₁ > 0. B такому випадку нерівність (6.26) виконується автоматично. Для нерівності (6.27) одержуємо

таким чином, воно також виконується автоматично.

To же має місце й для нерівностей (6.22) і (6.25), оскільки, якщо D(p) —

убутна функція, то

а якщо S(p) — зростаюча функція, то

отже, обоє нерівності з очевидністю виконуються.

Таким чином, припущення Вальраса й Маршалла дають однаковий результат у нормальному випадку.

Розглянемо тепер динаміку поводження ціни, тобто питання про асептичної стійкості. B відповідності із припущенням Вальраса одержуємо

де f — функція надлишкового попиту, має той же знак, що й надлишковий попит, і f(0) = 0, тобто нульовий надлишковий попит означає, що система перебуває в рівновазі f’(0) > 0, тобто при переході від негативних до позитивних значень функція зростає.

де

Для рішення диференціального рівняння (6.28) необхідно знати точний вид функцій f, D, S. Для спрощення розрахунків проведемо лінеаризація функцій, розкладаючи з у ряд Тейлора до першого ступеня в околиці крапки рівноваги (D = S, p = p_e) Одержуємо

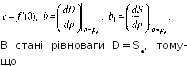
(6.30)

(6.31)

з характеристичним коренем

(6.32)

Загальне рішення рівняння (6.31) будемо шукати у вигляді:

де константу C знаходимо з умови

Константа C дорівнює первісному відхиленню від станів рівноваги.

Таким чином, остаточно маємо

Рівновага є асимптотичними стійким, якщо при збільшенні t ціна p(t)ap_e. Це можливо, якщо відхилення ∆p = p(t)-p_e →0, тобто, з формули (6.37) (р₀ - р_е)е^с(b-b1)t →0, можливо тільки, якщо c(b – b₁) < 0. Оскільки c =f(0) > 0, то одержуємо умову збіжності b – b₁< 0, що в точності збігається з умовою (6.26).

де g має той же знак, що і її аргумент, g(0) = 0, g'(Q) > 0. Далі одержуємо

Аналогічно для припущення Маршалла маємо диференціальні рівняння

Для того щоб виконувалася третя умова теореми, необхідно, щоб b – b₁ < 0, що збігається з умовою (6.26).

Зауваження.

1) B «простих ненормальних» ситуаціях, тобто коли одна з функцій попиту або пропозиції «ненормальна», припущення Вальраса й Маршалла дають суперечливі умови стійкості; а в «зовсім ненормальних» ситуаціях (обидві функції ненормальні) - однакові.

2) Стійкість рівноваги істотно ускладнюється, якщо розглядати запізнювання реакції попиту (або пропозиції) на зміну ціни. Такі процеси описуються павутиноподібною моделлю.

Проведемо аналіз стійкості загальної рівноваги Вальраса. B загальному випадку функції попиту та пропозиції кожного товару залежать від цін на всі товари, тобто

(6.40)

де E — надлишковий попит на товар j.

Стан рівноваги означає, що надлишковий попит на всі товари дорівнює нулю. Цьому стану відповідає вектор рівноважних цін р^е.

Назвемо стійкість недосконалої, якщо при зміні ціни товару j всі інші ціни змінюються так, щоб на всіх інших ринках рівновага відновилася.

Умова стійкості означає, що ціна викликає зміну власного надлишкового попиту в протилежному напрямку, тобто

(6.41)

Знайдемо умову недосконалої стійкості. В точці рівноваги маємо

(6.42)

де

Припустимо, що ціна товару j змінилася та інші ціни також змінилися відповідно до умови недосконалої стійкості. Тоді одержуємо систему з m рівнянь із m невідомими dp_і:

(6.43)

Вирішуючи систему отримаємо

(6.44)

де - якобіан функції надлишкового попиту,

D_jj – головний мінор (m – 1)-го порядку із D.

Із (6.44) отримуємо

(6.45)

разом з (6.41) одержуємо <0 отже, D і D_jj повинні бути різного знака для всіх j.

Назвемо стійкість досконалу, якщо при зміні ціни одного товару виконується одне із двох умов:

1) всі інші ціни залишаються незмінними;

2) підмножина з k інших цін відновлює рівновага, а інші (m - k - 1) залишаються незмінними.

Стійкість у першому випадку означає, що

(6.46)

звідки одержуємо, що

і, отже,

(6.47)

Для визначення умов стійкості в другому випадку припустимо спочатку, що ціна p_j змінюється, а інша ціна р_h змінюється так, щоб відновити рівновага на ринку h. Тоді одержуємо

(6.48)

далі,

B силу (6.41) и (6.47) отримаєм

Умова (6.51) повинне виконуватися для будь-якої пари (j, k), оскільки в процесі можуть брати участь будь-які два ринки. Таким чином, всі головні мінори другого порядку повинні бути негативними.

Продовжуючи далі, одержимо, що для зробленої стійкості необхідно й досить, щоб всі головні мінори порядку r з визначника D мали знак (-l)^r, r=1, ...,m.

де функції F_j мають той же знак, що й аргумент, і

Для з'ясування питання про асимптотичної стійкості розглянемо систему (6.52)

Де ціна рівноваги.

Позначимо

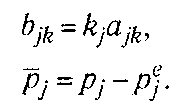
Тоді система може бути переписана у вигляді

(6.54)

Загальне рішення системи (6.54) має вигляд

(6.55)

де λ_і, K_і — відповідно власні числа й власні вектори матриці В.

Асимптотична стійкість означає, що _j,=0 і дійсні частини всіх власних чисел у рішенні (6.55) повинні бути негативними.

B частці випадку двох ринків одержуємо характеристичне рівняння для системи

Умови зробленої стійкості (6.47) і (6.51) у такому випадку є достатніми умовами й асимптотичної стійкості. Однак для моделей більше високої розмірності ці умови не є ні необхідними, ні достатніми, крім особливих випадків: симетрія (a_ij = а_ji); чиста взаємозамінність (a_ij <0, а_ji > 0); вплив, що вирівнює, своєї ціни (а_ii < 0).

КОНТРОЛЬНІ ПИТАННЯ

1. Основні положення моделі Харрода - Домара.

1. Поняття технологічного темпу приросту випуску продукції.Визначення найкращого темпу приросту споживання.

2. Основні припущення моделі В. Леонтьева.

3. Загальний вид рівнянь динамічної моделі В. Леонтьева.

4. Поняття про допустимість стану й траєкторії моделі В. Леонтьева.

5. Рішення моделі В. Леонтьева у випадку відсутності екзогенного споживання й з його обліком.

6. Розходження в поводженні моделі В. Леонтьева при зміні структурних коефіцієнтів моделі.

7. Дискретна й безперервна моделі попиту та пропозиції.

10. Методи рішення дискретної й безперервної моделі попиту та пропозиції.

11. Модель рівноваги Вальраса.

12. Стійкість загальної рівноваги Вальраса.

РОЗДІЛ 7

НЕЛІНІЙНІ ДИНАМІЧНІ МОДЕЛІ

7.1. МОДЕЛІ ЕКОНОМІЧНИХ ЦИКЛІВ ГУДВИНА

Перейдемо тепер до більше складним, нелінійним, моделям, що описують виникнення циклічних коливань в економічному розвитку. Починаючи із простої моделі, запропонованої Гудвином, будемо послідовно неї ускладнювати, з огляду на все більшу кількість факторів.

Будемо вважати, що в будь-який момент часу t економіка має у своєму розпорядженні основний капітал ДО, що включає заводи, устаткування й т.д. його обсяг міняється зі швидкістю, рівної відношенню чистих капіталовкладень до загального зношування за даний період часу. Джерелом економічного доходу є обсяг виробництва Y і споживання С. Ці величини зв'язані між собою співвідношеннями

де а й p — дійсні контрасти, такі, що а < 0, p < С. З рівняння (7.1) видно, що між обсягом виробництва й споживанням існує лінійна залежність. Рівняння (7.2) означає, що вся випущена продукція, що, або споживається, або йде на розширення виробництва. Припустимо далі, що основним капіталом Аунравляют так, щоб підтримувати на рівні, пропорційному обсягу виробництва. Якщо R — бажаний рівень основного капіталу в момент часу t, то

де в - деякий параметр.

Представимо перший варіант моделі:

звідки

Зі співвідношення (7.3) видно, що періодичне поводження величини Y (або K) може виникнути як наслідок коливань у капіталовкладенні К. B свою чергу, ці коливання виникають із прагнення зрівняти величини (бажаний рівень основного капіталу). Нехай проводиться екстремальна політика капіталовкладень:

де К і ДО не залежать від часу.

Розглянемо сутність формули (7.6). Якщо основний капітал менше бажаного рівня, то умова (7.6) відповідає максимальному рівню капіталовкладень (перша умова в (7.6)). Якщо ж бажаний рівень перевищений, то капіталовкладення нульові, а основний капітал амортизується зі швидкістю K₂ (третя умова (7.6)). Розумно допустити, що при максимальному рівні капіталовкладень швидкість, з якої можуть будуватися нові підприємства, більше швидкості амортизації й старіння, тобто з рівняння (7.3) та (7.6) слідує, що

, якщо K<R

, якщо K=R

, якщо K>R

Нехай R₂ < K < R₁, так що при t = 0 виконується R = R_r Тоді рівень капіталовкладень дорівнює k_x > 0, величина k росте, а У залишається постійним Q (рис. 7.1 )до тих пір, поки не досягнеться рівняння. R приймає

значення R_0. Тепер

К_1> К₂

K = R₁ > R ⁼ R₀. Таким чином, K миттєво міняється від величини k_x до -k₂, a R — від R₁ до R₂- B той же самий момент, відповідно до формули (7.5), різко падає обсяг виробництва. Тепер убиває до величини R₂. Аналогічне міркування показує, що R при цьому стає рівним R₁, так що K ⁼ R₂ < R — R₁, і величина K знову стає рівної Основний капітал K знову зростає до R₁, і цикл замикається. Таким чином, обидві величини — Kvi Зазнають-у^-випробовують коливання, як показано на мал. 7.1.

Мал. 7.1. Коливання величин K і Y часу для політики капіталовкладень виду «коштуй - іди»

Розглянемо поводження моделі на фазовій площині (K,K), представленої на мал. 7.2 рух відбувається по прямолінійних відрізках BC і DA, де K — і K⁼ -k₂ відповідно. Перегони від A до B і від C до D відповідають розривам функції Y, показаним на мал. 7.1.

Описана модель добре відбиває економічний цикл. Бo час періодів капіталовкладення обсяг виробництва високий і економіка перебуває в періоді підйому. Коли ж капіталовкладення відсутні, обсяг виробництва падає, і економіка перебуває в стані депресії. Однак у розглянутої моделі є багато недоліків. Так, перегони в капіталовкладенні й миттєвій реакції на них з боку обсягу виробництва Y (див. формулу (7.5)) не відповідають дійсності. Крім того, з умови k_{ = k₂ треба, що періоди спаду значно перевищують періоди підйому, чого в реальності не спостерігається. Більше того, у моделі відсутній загальний ріст економіки, тому що обсяг виробництва, основний капітал та інші показники періодично приймають колишні значення.

Мал. 7.2. Подання стану економіки на фазовій площині (перегони величин зазначені пунктиром)

Передбачимо, що в момент часу t = r, дисперсії закінчується і відбувається перехід від (7.11) к рівнянню (7.10), тоді залежність величини У от времени t для фази підьома буде мати вид:

Приведемо другий варіант моделі. Модифікуємо модель, з огляду на такі фактори:

1. вплив капіталовкладень на ріст обсягу виробництва;

2. відсутність стрибкоподібних змін у капіталовкладенні. Для обліку першого фактора змінимо рівняння (7.5) так, щоб в функції У не було стрибків навіть у тому випадку, коли величина K їх має. Це можна зробити замінивши рівняння (7.5) на

де e — деяка позитивна константа.

Зрозуміло, що новий додаток в (7.9) спричиняє затримку в реак­ції функції У на змінення K- Із рівняння (7.9) знаходимо:

, якщо K>R

, якщо K<R

З рішення (7.12) видно, що величина У не зростає миттєво до значення ф+ Ј,)/(1 — a), a прагне до нього при t ^ °°. Помітимо, що час, що потрібно для того, щоб функція Y(t) із заданою точністю став рівній цій величині, цілком залежить від параметра е. Аналогічним образом, рівняння (7.11) згладжує стрибкоподібне падіння Y(t) (див. мал. 7.1) наприкінці періоду підйому.

Ліквідуємо тепер розриви в капіталовкладенні, тобто «зм'якшимо» раптовий перехід від K — k_x до К— ~к₂ (і навпаки), що виникає, коли K стає рівним R.

Розглянемо ту частину капіталовкладень, що виникає зі зміною обсягу виробництва. Зміни в капіталовкладенні відбувається тому, що ми хочемо підтримувати основний капітал на рівні бажаного капіталу. Зміна величини У викликає зміна R, що, у свою чергу, тягне зміну K- Ясно, що якби нам вдалося підтримувати K = j, те виконувалося б і співвідношення K = R. Але такого бути не може, оскільки рівність не може виконуватися при всіх значеннях t, тому що величина K має верхню границю k₇ і нижню границю (~k₂). Тому ми припустимо, що K — y(Y)- Вид функції y(Y) зображений на мал. 7.3.

Як видно з малюнка, змушені капіталовкладення в(В) близькі до ідеального рівня у У для малих величин В, а при більших У| вони обмежені величинами k_x до (—k₂). Помітимо, що функція в(В) — У немонотонна (тобто має «горби») і схожа на кубічну параболу. Коли капіталовкладення досягають свого максимального значення, основний капітал перестає задовольняти вимозі K - y.

Це означає, що K треба вибрати у вигляді:

^де (Y) — індуковані капіталовкладення, викликані зміною обсягу виробництва, L — вплив інших капіталовкладень.

Тоді рівняння (7.9) треба замінити на:

Щоб одержати графік функції Y залежно від Y, потрібно зрушити функцію

Ця крива, разом із пропозицією про перегони, повністю описує поводження другої моделі. Крапки, що відповідають всім можливим станам моделі, лежать на цій кривій, і знак показує, зростає або убуває величина Y. Таким чином, рух крапки, що визначає стан системи, повинне відбуватися в напрямках, зазначених стрілками. Крапка ф + L; 0) є, отже, нестійкою нерухомою крапкою системи. Із крапок C і A за аналогією з мал. 7.2 повинні відбуватися перегони. Припустивши, що перегони походять із A в B і з C в D, одержимо релаксаційні коливання для Y.

Тепер розглянемо третій варіант моделі. Урахуємо тепер запізнювання реальних капіталовкладень щодо ухвалення рішення про їхню необхідність. Це означає, що індуковані вкладення в момент часу t насправді залежать не від Y(t), а від — ь), де v — запізнювання.

Тоді замість рівняння (7.14) треба писати:

Якщо ввести x = t — v, з (7.15) одержимо:

Розкладемо ліву частину рівняння (7.16) по ступенях u:

Або

L

Якщо вважати, що fJ + L = const і ввести:

це (7.18) можна переписати у вигляді зберігши лише члени першого порядку по v, тоді знаходимо:

Введемо нову залежну і незалежну змінливу співвідношення:

Тоді замість (7.20) маємо:

Якщо [e +(1 — a)v]<

то функція %(x)

схожа на кубічну параболу, а (7.23) — рівняння типу рівняння Релея

і в нього є стійкий граничний цикл, тобто мають місце автоколивання.

7.2. ДИНАМІКА КОРИСНОСТІ СПОЖИВЧИХ БЛАГ

Розглянемо інший приклад моделі, у якій використається інший підхід до проблеми оцінки впливу економічних, зокрема виробничих циклів, на характеристики економічної системи. B представленій нижче моделі враховується вплив виробничих циклів на динаміку корисності споживчих благ. Нехай відома сукупність споживчих благ визначеності (будемо думати матеріальні блага) x, j = 1, m, які здобуваються й споживаються економічним суб'єктом. B відповідності з теорією суб'єктивної корисності стратегія споживання цього блага залежить від функції його корисності U = U(X) (X — вектор споживчих благ); вид і форма кривої функції корисності визначає динаміку споживання X(t), де t — час. Оскільки споживання змінюється в часі, те маємо U = Y[X(t)], тобто функція корисності споживчих благ залежить від часу опосередковано — через динаміку їхніх обсягів. Даний методологічний прийом, що дозволяє зв'язати величину функції корисності згодом, досить важливий і цікавий, тому що незважаючи на те, що в економічній теорії властивості статичної функції корисності U~ U(X) досить добре вивчені (як правило, такі залежності виражаються логарифмічними й статечними функціями), закономірності зміни динамічної функції корисності U= U(t) дотепер практично не розглядалися. Таким чином, залежність U= U[X(t)] дозволяє «динамізірувати» подальші побудови.

Враховуючи сегментованість товарного ринку й множинність споживчих благ, агрегатна функція корисності U може бути представлена у вигляді адитивної функції корисності:

,

де U - приватна корисність споживаного блага; вагові коефіцієнти р задають шкалу відносної значимості розглянутих благ (аналогічні побудови можливі й при розгляді макроекономіки в цілому; у цьому випадку й буде характеризувати добробут суспільства, a p = U/d — граничну соціальну значимість той групи споживчих благ). Незважаючи на те, що даний приватний вид агрегатної функції корисності досить спрощено відбиває дійсність, його розгляд є позитивним підходом до принципового розуміння процесу через простоту наступних формальних конструкцій. Помітимо, що в теоретичних дослідженнях різні модифікації адитивних функцій корисності використаються досить широко. B подальшому без втрати ступеня спільності для проведеного аналізу будемо розглядати лише два споживчих блага: i і 1. Такий прийом цілком правомірний, тому що будь-який набір благ може поєднуватися в невелике число групових благ. Таким чином, згортка всього споживчої безлічі у двохфакторну конструкцію - це лише Проблема відповідного способу агрегування (узагальнення на і-й випадок буде представлено нижче).

Виходячи зі сказаного, можна записати наступні умови першого й другого порядку для функції корисності:

де A₁ = d Zd₁ ; B₁ = d²V_t4dxxf; G₁ = dUt; R₁ = d²U_t4d? : C= d/dt; D= cPU/df. Зрозуміло, що в загальному випадку величини A₁, B₁, G₁₁R₁, З, D залежать від часу. Таким чином, система (7.26) дозволяє визначити стратегію споживача x. (t) при заданих времен-ньгхтраекторияхА(/),В₍(0> G,(t),R,(t), C(t),D(t). ПриэтомА.(^) і B_t(t) отражаютдинамику смаків і переваг споживача в часі, G₁(I) і R_t(t) фіксують швидкість і прискорення, з якими споживач припускає нарощувати (зменшувати) корисність від володіння благом X₁, a C(t) і D(t) характеризують швидкісні властивості росту агрегатної функції корисності.

Якщо ввести характеристику темпу прискорення агрегатної корисності в часі а = D/C, то система (7.26) редукується до наступного рівняння:

Розглянемо приватний, але дуже важливий випадок. Так, якщо r = З/U— темп приросту корисності й він постійний у часі, то а = r. B моделі (7.27) показник дозволяє відобразити напрямок зміни агрегатної функції корисності з урахуванням ефекту масштабу споживання. Нехай приріст приватної корисності 1-го блага також стабільний: G₁ = const. Тоді R= 0 і рівняння (7.27) у цьому випадку приймає вид:

Увівши показник абсолютної антипатії до споживання k-_t = - B₁ *JA₁ , позначивши з = W₁G₁/Jp₁A₁ і думаючи з = const, а також опускаючи надалі індекс i, рівняння (7.28) остаточно зводиться до наступного виду:

Дана модель є досить грубою, будучи лише першим наближенням модельованого процесу. B подальшому рівняння (7.29) уточнюватиметься і деталізуватиме, проте його математична структура залишиться незмінною.

B відповідності з ортодоксальною теорією корисності A > 0 (у силу аксіоми насичення), a B<0 (у силу закону Госсена). Одночасно із цим смаки й переваги споживачів, на думку А. Маршалла, згодом змінюються завдяки виробленню відповідних споживчих звичок («пристрастей» і «антипристрастей»), що означає зміну A₁, B₁, p і р у часі. При цьому якщо A₁ і R характеризують криву корисності залежно від монотонної зміни x, те величини C і D дають ясну характеристику корисності залежно від монотонної зміни часу. B цьому змісті рівняння (7.29) задає траєкторію споживання залежно від мінливих смаків і пристрастей споживача при реалізації їм «примусової» (цільовий) стратегії відносно збільшення свого добробуту. Однак відповідно до економічної доктрини Беккера — Стиглера, що у цей час домінує в економічній теорії, смаки й переваги споживача покладаються стабільними в часі. Це еквівалентно тому, що показники k і ю в рівнянні (7.29) не залежать від часу й разом з r виступають як параметри моделі.

Тут і далі при вивченні закономірностей динаміки споживання ми будемо абстрагуватися від тих соціально-психологічних факторів, які роблять на неї який-небудь вплив. Випливаючи цієї лінії міркування, ми не розглядаємо роль так називаного людського капіталу, що у теорії Стиглера - Беккера має ключове значення. Подібна методологічна «вузькість» проведеного аналізу представляється цілком виправданої, тому що нас цікавлять винятково тимчасові аспекти споживання. Тим самим центр ваги теоретичних побудов переноситься на з'ясування «зовнішніх» сил, що формують динаміку споживання, а не «внутрішніх» факторів, які самі випробовують найсильніші впливи ззовні. Іншими словами, динаміка споживання виявляється залежної від «чистих», рафінованих преференцій суб'єкта відносно споживчих благ і не залежить від структури його постійно, що еволюціонує особистості. Незважаючи на настільки явне огрубіння дійсності, саме такий підхід є ефективним, тому що дозволяє зрозуміти закони споживання в абсолютно стабільній соціально-психологічному середовищі, що є необхідним першим кроком до вивчення більше складних економічних ефектів.

Таким чином, рівняння (7.29) описує динаміку споживання i-ro блага в стаціонарній економіці, під якою в широкому змісті слова розуміється економіка з постійними в часі характеристиками росту. Саме такий тип економіки буде розглядатися в даній роботі. Подібний підхід дозволяє довести наступне попереднє твердження про народження споживчої флуктуації в умовах стабільності смаків економічних агентів: стратегія, що забезпечує споживачеві постійний заданий темп приросту добробуту (корисності) при стабільності його смаків і переваг, описується рівнянням (7.29); при виконанні закону Госсена (закону убування граничної корисності) і аксіоми ненасичення для G₁= const > 0 і 4k(p/p) (Gj)>t дана стратегія носить принципово нестійкий характер.

Змістовно сформульоване твердження означає наступне: при певній споживчій консервативності економічний агент, що прагне нарощувати свій добробут (корисність) досить плавним образом, виявляється, повинен здобувати й споживати блага аж ніяк не рівномірно. Причому динаміка x(t) характеризується досить різною зміною «провалів» у споживанні з настільки ж стрімкими сплесками споживчого попиту (мал. 7.5).

Отже, стабільність смаків економічного агента сама по собі, як виявляється, не захищає від виникнення ендогенних флуктуацій у попиті й споживанні. Даний висновок на перший погляд представляється парадоксальним, тому що правомірно було б очікувати, що в подібних умовах споживча стратегія повинна виражатися гладкою функцією. Очевидно, це одні з тих випадків, коли найкоротший шлях не є оптимальним.

Помітимо, що твердження сформульоване для ситуації з досить більшим числом ступенів волі. Деякі економічні фактори відбиті в параметрах рівняння (7.29). Так, наприклад, термін служби товару, а також інтенсивність його фізичного й морального зношування непрямим образом акумулюються в показнику абсолютної антипатії до споживання. Однак у моделі (7.29) не враховуються бюджетні обмеження, можливість створення запасів, дискретність економічних угод і процесів споживання й ціноутворення, не відображені цінові ефекти, а також динамічні ефекти заміни й взаємодоповнюваності благ (у цьому змісті k являє собою згортку «чистих» споживчих смаків і преференцій, а показник r — згортку швидкісних показників стратегії споживача відносно свого добробуту). B реальності ж всі перераховані обмеження фігурують у якості активних, що деформує гіпотетичні траєкторії споживання, а також самі споживчі установки. Формально це означає, що облік зазначених ефектів буде сприяти аберації вихідній кривій x(t) (мал. 7.5) і «зрізати» або, навпаки, підсилювати флуктуації часу (7.30).

,

де A = 4ka>-r² є біфуркаціонною комбінацією. Рівняння (7.30) представляє квазіперіодичну функцію.

Далі поведемо аналіз того, яким чином споживчі норми й звички впливають на форму траєкторії споживання.

По-перше, в умовах сформульованого твердження обсяг споживання згодом скорочується, а маючи місце коливання відбуваються навколо позитивного лінійного тренда, що володіє магістральним, що притягає властивістю фис.7.5).

По-друге, чим більше величина абсолютної антипатії до споживання й чим нижче темп приросту агрегатної функції корисності, тим більше частота коливань обсягу споживання. Це означає, що чим вище гранична корисність споживаного блага й чим слабкіше виражений закон Госсена, тим нестійкіше споживча стратегія, тобто при низькій суб'єктивній оцінці блага економічний агент менше схильний до «шараханню» у споживанні даного блага, період народження споживчі флуктуації розтягується й динаміка x(t) має більше стабільний характер. Крім того, частота флуктуації зростає в міру збільшення соціальної значимості альтернативного /-ro блага в порівнянні з /-м благом.

По-третє, чим більше абсолютна антипатія до споживання й соціальна значимість / -го блага, тим вище амплітуда економічних коливань, тобто чим вище гранична корисність блага й чим слабкіше відбувається насичення попиту в міру споживання, тим більше розмах коливальних тенденцій у динаміку споживання.

По-четверте, чим нижче темп приросту агрегатної функції корисності, тим повільніше відбувається зниження обсягу споживання.

Причина, що викликає споживчі коливання, полягає у своєрідному, досить складному, способі тимчасового зважування (дисконтування) економічним агентом потоку споживання. B якості коефіцієнтів, що дисконтують, виступають характеристики 1 -ro і 2-го порядків приватної функції корисності, що й відбито в рівнянні (7.30). Таким чином, споживчі цикли викликаються чинністю закону Госсена н аксіоми ненасичення.

Якщо розглядати спрощений випадок, коли має місце тільки один товар, то стратегія споживання буде також описуватися рівнянням (7.30) при з = 0. B цьому випадку траєкторія споживання задається монотонно зростаючою функцією без екстремумів. Це означає, що процес споживання є стабільним лише в найпростішому випадку для n = 1. При цьому даний процес надзвичайно нестійкий, і найменше стороннє збурювання (поява з 0) може вивести систему зі стаціонарного режиму, збиваючи її на детерміновані циклічні коливання й ведучи до перебудови фазового портрета рівняння (7.30). Таким чином, одна з основних причин утворення споживчих флуктуацій - наявність безлічі благ. Саме дія додаткових благ (не важливо, комплементарних або взаємозамінних) і є тим «підбурництвом спокою», що змушує економічного агента дотримуватися складної динаміки споживання.

З огляду на специфіку конфігурації з і те, що dilJd = -pJp^ відношення P₁Zp₁ являє собою не що інше, як граничну норму заміщення корисностей відповідних видів споживчих благ. Отже, правомірно попереднє твердження про те, що специфіки дисконтування споживання, відбивана рівнянням (7.29), є необхідною умовою народження економічних флуктуацій, а наявність декількох благ, що володіють властивістю взаімокомпенсуючої корисності - достатньою умовою.

Коротко зупинимося на тім факті, що рішення (7.30) породжує два цікавих парадокси.

Перший пов'язаний з понижаючим характером лінійного тренда (магістрального променя) в умовах експонентного росту агрегатної корисності й лінійного зростання альтернативного блага, другий — з біфуркацією рішення рівняння (7.29) при переході від а = к>0, що коли монотонно зростає функція трансформується в спадну траєкторію з періодичними биттями. Прокоментуємо дані ефекти. Цей парадокс досить добре відомий в економічній теорії. Яскравими прикладами такого роду динамічних ефектів є теореми Столпера - Самуельсона й Рибчинського у формі Р. Джонса: у Рибчинського екзогенні зміни в темпах приросту обсягів факторів виробництва приводять до непропорційно більших змін в обсягах випуску; у Столпера - Самуельсона екзогенні зміни в темпах приросту товарних цін обумовлюють більше сильну реакцію цін макрофакторів. Таким чином, у розглянутій нами моделі (7.29) має місце, по суті справи, той же ефект акселерації Р. Джонса, що й у простих, малорозмірних моделях економічної рівноваги.

Другий парадокс також добре вивчений у різних розділах математики й насамперед у теорії біфуркацій. C точки зору варіаційного обчислення, динамічного програмування й оптимального керування нетривіальна форма траєкторій, що забезпечують реалізацію простих цільових настанов, є також цілком природним явищем. B якості найпростішої аналогії отриманого результату можна привести спосіб руху корабля, що випливає заданим курсом: борючись із різними підводними плинами й потоками вітру, капітан корабля змушений лавірувати навколо заданої лінії руху, постійно відхиляючись від її, що й приводить до хвилеподібної траєкторії шляху проходження судна.

Розглянемо модифікацію колишньої моделі, що враховує генерування виробничих циклів, що роблять вплив на формування споживчих благ. Отримані раніше результати досить наочні, але, як указувалося вище, справедливе лише для частки випадку агрегатної функції корисності. B цього зв'язку виконаємо деякі важливі узагальнення. Для цього будемо розглядати, як і колись, двухфакторну схему, де U=Ufx(t),x/t)J — агрегатна функція корисності довільного виду. B відмінність від попереднього випадку, де функція корисності залежала від обсягу споживаних благ, тут вона залежить ще й від способу комбінації (виду взаємозв'язку) цих благ. Інакше кажучи, розглянутий випадок дозволяє в явному виді врахувати можливі взаємодії між факторами споживання. Тоді умови 1-го й 2-го порядків для функції корисності приймуть наступний вид:

де U₁ = d/dxr, а, = 3U/dx, b=&U/&x:, b=oPU/dxf ; b=cFV/dx_i dx,.

B відповідності з ортодоксальною теорією а > 0 і а, > 0 (аксіома ненасичення), Ь_и< 0, b_tl< 0 (закон Госсена), b_u > 0. При цьому всі показники використаються в канонічній (класичної) формі. Система (7.31), як і в попередньому випадку, редукується до рівняння:

Тепер, як і раніше, приймемо ряд позначень, що спрощують, і гіпотез: м = const, _X1 = X - const, k = - bu /а. — абсолютна антипатія до споживання 7-го блага; 9 = b „ /а,-, про = b_u Ia₁, ц = dx_t /dx_t — гранична норма заміни г'-го блага (відповідно до принципу взаємозаміни ц < 0); X, 9, про , ц и k також є константами. Тоді X₁ =0 і рівняння (7.32) приймає остаточний вид (індекс / для простоти опускаємо):

Нескладно бачити, що рівняння (7.33) за структурою ідентично рівнянню (7.29); розходження між ними складається лише в більше складній конфігурації параметрів (7.33). Як і в рівнянні (7.29), рішення (7.33) біфурцирує до нестійкого типу при порушенні умови

,

яке може трактуватися як умова відсутності економічних коливань (відповідно порушення (7.34) умова 1-го порядку нестійкості економічного розвитку). Умова 2-го порядку для виникнення періодичні флуктуації в споживанні x задається біфуркаціонною нерівністю

>

Аналіз знаків параметрів, що фігурують тут, показує, що при K > 0 і r > 0 ліва частина (7.35) завжди більше нуля. Отже, строге виконання нерівності (7.35) аж ніяк не тривіально й можливо лише при певнім сполученні швидкісних характеристик моделі (7.34) і набору вхідних у неї показників еластичності. Нескладно бачити, що, як і у випадку моделі (7.29), в (7.34) основним фактором, що обурює, служить ефект заміни двох благ. Таким чином, у моделі (7.34) у явній формі фігурують перехресні ефекти взаємозаміни й компліментарності. Дані ефекти доповнюються показниками Ь_и і й .

Розглянуті динамічні ефекти в сфері споживання можуть бути поширені й на виробничу сферу. B цьому випадку замість споживчих благ x. і X₁ будуть фігурувати традиційні макрофактори — праця й капітал, поняття корисності (добробуту) заміняється на випуск продукції, а сама функціональна залежність U — U[x[t), X₁Q)] перетворюється у звичайну виробничу функцію. Оскільки рівняння (7.36) виведено для функцій довільного виду, то воно щиро й для таких залежностей, як функція Кобба — Дугласа й CES-функція, традиційно використовуваних у макроаналізі. Тоді в новій інтерпретації г характеризує темп економічного росту, k означає абсолютну антипатію до використання розглянутого макрофактора. При цьому аксіома ненасичення перетворюється в постулат про ненегативну граничну продуктивність (ефективності) макроресурсу, закон Госсена - у закон убутної віддачі витрат, а принцип заперечності норми заміни споживаних благ - у принцип заперечності граничної норми заміщення виробничих факторів. Уведені припущення щодо стабільності коефіцієнтів у рівнянні (7.34) змістовно означають відсутність науково-технічного прогресу.

Помітимо, що двохфакторна модель (7.34) надзвичайно зручна й інформативна саме у виробничих термінах. Так, наприклад, для мікроекономічної ситуації ефект виникнення ендогенні флуктуації означає наступне. При постійних у часі приростах інвестицій (для визначеності аналізу як екзогенний фактор будемо розглядати саме цей виробничий ресурс) досить активне стаціонарне зростання виробництва фірми можливий лише при нестабільній динаміці використання робочої сили. Іншими словами, стабільні капіталовкладення приводять до стійкого зростання виробництва тільки при досить гнучкій стратегії відносно робочої сили, що виражається в оперативному рятуванні фірми від її надлишків і, навпаки, зверхшвидкому заповненні вакансій, що з'являються. Отже, стаціонарне розширення виробничих можливостей фірми можливо тільки завдяки високому ступеню адаптації до всіх нюансів технологічного процесу хоча б одного з використовуваних нею макрофакторів. При цьому в розглянутій теорії фірми, як і в теорії споживання, одним із джерел, що провокують ендогенні коливання, є ефект ненульової еластичності заміщення праці й капіталу.

Зрозуміло, що дані міркування аналогічні й для макровипадку, коли розглядається стаціонарний ріст всієї макроекономіки. Якщо як ендогенний фактор, як і раніше, розглядати робочу силу, то дихотомічна умова (7.35) характеризує режим виникнення циклів зайнятості. Отже, при певній комбінації параметрів (7.34) цикли зайнятості (а відповідно й безробіття) є необхідною умовою стабільного розширеного відтворення. B зворотної ситуації, коли праця є екзогенним ресурсом, з рівняння (7.34) випливає теорія інвестиційних циклів, що припускає нерівномірність відновлення й завантаження виробничих потужностей. Крім того, з (7.30) треба, що амплітуда циклічних коливань аж ніяк не постійна, а тяжіє до періодичних катастрофічних скачок (мал. 7.5). Очевидно, такі крапки розриву в кривій x(t) відповідають періодам криз, коли виробництво й споживання скорочуються практично до нуля. B цього зв'язку можна констатувати, що загальна циклічна траєкторія розщеплюється на «малі» (незначні динамічні флуктуації) і «більші» (кризові спади) цикли.

7.3. ВПЛИВ ФЛУКТУАЦІЙ HA ДИНАМІКУ СПОЖИВЧИХ БЛАГ

Проведемо подальший аналіз моделей динаміки споживчих благ і розглянемо гранично загальний багатомірний випадок, тоді число споживчих благ (факторів) дорівнює т. Тоді функція корисності (макропродукт) U= U(X), де х, y = l,m і умови 1-го та 2-го порядку виглядають наступним чином:

де uj = Э U/dXj', b_js=d²U/dx.dx_s; j і s — індекси споживаних благ (виробничих факторів). При колишніх постулатах з обліком того, що xj = X j = const для всіх y' = 1, m — 1, шукана модель, що описує динаміку блага (фактора), приймає вид:

Тут, як і раніше, k_m =-b_mm /а_т — абсолютна антипатія до споживання (використанню) ш-го блага (фактора); ^_т]- = dx_n |dx -_} — гранична норма заміни блага (фактора). Для зручності також уведені позначення:

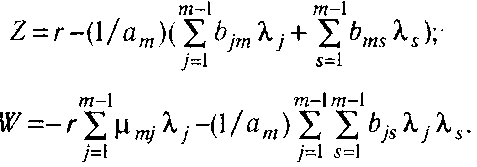
Уточнена в такий спосіб модель дозволяє сформулювати узагальнену теорему про народження ендогенні флуктуації в стаціонарно розширюється (стискальної) економіці.

Теорема. Якщо споживач (виробник) споживає (використає) m різних благ (факторів) таким чином, що m — 1 з них змінюються постійним темпом Xj = Xj, j = 1, m-1, а динаміка корисності (макропродукту) характеризується постійним темпом приросту r = ii|U, те стратегія споживання т-то блага (фактора) при дотриманні умови 8km>Z²Hocm принципово нестійкий характер.

Таким чином, при стаціонарному росту добробуту споживача (обсягу виробництва) і стабільному збільшенні споживаних благ (виробничих факторів) при зазначених умовах серед них завжди найдеться хоча б одне благо (один фактор), споживання (використання) якого буде піддано стабільним, незатухаючим флуктуаціям. Це означає також, що для моделювання системи виконується принцип взаємної динамічної залежності споживаних благ (виробничих факторів). Крім цього динаміка кожного елемента x залежить від широкого спектра перехресних еластичності. З огляду на залежність динаміки виробництва й споживання від особливостей руху цін, можна констатувати, що для моделювального процесу характерна система цін, тобто динаміка кожної мікроціни на споживче благо (виробничий ресурс) залежить від динаміки всіх інших цін і показників еластичності. Даний факт є принциповим, тому що, по-перше, він повністю погодиться із класичною теорією економічної рівноваги, а по-друге, даний результат отриманий виходячи з методологічних принципів, що трохи відрізняються від тих, на яких базується закон Вальраса. Крім того, слід зазначити, що в розглянутому випадку має місце явне посилення закону Вальраса, тому що останній охоплює одночасно сфери виробництва й споживання, у той час як модель (7.38) відбиває закономірності функціонування названих економічних секторів незалежно одне від одного. Таким чином, вальрасовский принцип загальної взаємозумовленості пронизує не тільки економічну систему в цілому, але і її окремі частини. Організуючим і синтезуючим початком подібного взаємозв'язку між неуважними в просторі й часі споживчими благами (виробничими ресурсами) є суб'єктивні економічні інтереси особистості споживача (виробника).

Рівняння (7.38) разом з формулами (7.39) і (7.40) дозволяє акуратно класифікувати групи факторів, які визначають характер динаміки розглянутого блага (фактора). Методологічно це означає розгляд можливості виконання дихотомічної умови 8km> Z². B загальному випадку можна виділити шість груп впливів, що обурюють.

Перша група — гранична корисність (продуктивність) a_m. Для найцікавішого випадку, коли r > 0 і 0, y' = l,m-l, гранична корисність (продуктивність) робить, як правило, що стабілізує вплив на динаміку х_т Це пов'язане з тим, що при збільшенні а_т збільшується значення параметра, що обурює, W у моделі (7.38), зменшується абсолютна антипатія k_m і зростає Z. Такий ефект зменшує ймовірність виконання умови, при якому виникають циклічні коливання. Таким чином, ріст а_т сприяє більше цілеспрямованому поводженню споживача (виробника).

Друга група — закон Госсена (закон убутної віддачі витрат) — {bjj),j ⁼ 1, тп — 1. Дана група факторів діє прямо протилежним образом першій трупі факторів у відношенні k_m і Z і аналогічним образом у відношенні W, тим самим дестабілізуючи економічну динаміку й збільшуючи розкид у діях споживачів і виробників.

Третя група — перехресні ефекти {b}, s. Даний фактор зменшує величину як W, так і Z. Таким чином, вплив розглянутих ефектів не очевидно. Однак, з огляду на квадратичну залежність Z у відповідній дихотомічній умові, очевидно, вони в більшості випадків гасять можливі циклічні коливання.

Четверта група — швидкість розростання розглянутої економічної системи (для макровипадку) або її сегмента (для мікровипадку) r. B більшості випадків даний фактор по досягненні деякого граничного значення сприяє більше стійким тенденціям у розвитку.

П'ята група — швидкість розростання елементів розглядаємої економічної системи (для макровипадку) або її сегмента (мікровипадку) {X),j = 1, m — 1. O впливі даної групи факторів у загальному випадку нічого не можна сказати, тому що все залежить від конкретних значень приростів і їхньої комбінації між собою.

Шоста група — принцип взаємозамінності споживчих благ (принцип взаємозамінності виробничих факторів) {ц}. Чим сильніше проявляється даний закон, тим більше Ww, отже, тим вище ймовірність народження ендогенні флуктуації. Даний висновок представляється найцікавішим і важливим, тому що він, по суті, означає наступне: чим сильніший ефект заміни, тим сложней економічна динаміка. Такий результат повністю погодиться з основними положеннями сучасної економічної теорії.

Таким чином, розглянуті групи факторів свідчать про те, що їхній вплив на динаміку х_т досить неоднозначно й може бути як завгодно різноманітним. Так, наприклад, групи r і {Xj) утворять своєрідні динамічні потенціали системи, які балансуються досить складним образом, у той час як перша, друга, третя й шоста групи факторів являють собою сукупність дисконтів, за допомогою яких і відбувається дане балансування. При цьому, як видно з рівняння (7.38), прискорення споживання х_т і квадрат його швидкості (x_m )² зважуються за допомогою простих коефіцієнтів, які не включають динамічні характеристики інших благ (факторів). Даний факт є цілком природним, тому що компоненти х_т і (x_m )² відображають більше тонкі ефекти (2-го порядку) і лише нівелюють можливий динамічний дисбаланс. B цьому змісті параметри при них утворять «повільну» складову системи дисконтів, у той час як параметри Z і W, акумулюючи в собі збурювання 1 -го порядку, залежать від динамічних факторів r і {X.} і утворять тим самим «швидку» складову.

B цілому розглянуті групи факторів дозволяють усвідомити собі, які «сили» економічної системи, взаємодіючи й «борючись» між собою, приводять до нових складних ефектів. Той факт, що переважна більшість цих «сил» являють собою універсальні закони й принципи економічної теорії, свідчить про плодотворність використовуваного в даній роботі підходу, що продовжує традицію сучасного маржиналізма.

Зупинимося тепер на біхеористичном аспекті аналізу. Справа в тому, що народження ендогенних коливань відбувається лише при: виконанні дихотомічної умови 8k_m2W> Z². B інших режимах система має цілком задовільну динамічну стійкість. Логічно поставити запитання: у якому ступені підтримка динамічної стійкості системи є регульованим процесом? Відповідь на це питання випливає із проведеного аналізу груп факторів, що впливають на характер дихотомії. B широкому змісті регулюванню підлягають всі шість груп, у вузькому змісті - параметри r і {Xj}, тому що перша, друга, третя й шоста групи факторів у реальності слабко управляємі й утворять комплекс псевдо екзогенних соціально-економічних умов, на тлі яких споживач (виробник) реалізує свої стратегії r і {^!.Маніпулюючи саме обсягами споживання {X.} і акуратно підбудовуючи під , них свій цільові настанови відносно темпу росту r, економічний агент може впливати на процес у тім або іншому напрямку. При цьому практично завжди можна за рахунок більше помірного споживання деяких благ (факторів) зберігати стаціонарність процесу. І навпаки, зайва «жадібність» у використанні деяких благ (факторів) породжує цикли виробництва й споживання. Дані висновки трохи нові й несподівані, мабуть, лише стосовно до сфери споживання. Що стосується виробничої сфери, те щодо її можна вважати вже устояну думку про дестабілізуючий вплив економічних «перегрівів» на стійкість економічного розвитку.

Розглянемо тепер нестаціонарний випадок для економіки, що припускає наявність екзогенних шоків. Вище розглядалася стаціонарна економіка, для якої виявилося можливим побудувати цілком задовільну теорію економічних флуктуацій. Однак умови стаціонарності, що накладають насамперед на такі динамічно нестійкі показники, як а й Xj, у реальності абсолютно нездійсненні. Проте, як показав аналіз, навіть у стаціонарних умовах можливе виникнення циклічних економічних коливань. Саме в цьому контексті має принципове значення сформульована теорема про народження ендогенних флуктуацій.

Що ж торкається питання про можливості побудови загальної теорії для нестаціонарного випадку, то на нього можна дати негативна відповідь. Так, наприклад, якщо припустити, що всі параметри в моделі (7.38) змінюються в часі по якихось своїх власних законах, то в цьому випадку динаміка х_т буде описуватися рівнянням:

Оскільки залежність коефіцієнтів (7.41) від часу строго задана, те це рівносильно наявності в системі екзогенних шоків (збурювань), які й формують ендогенну динаміку x_m (t).

Шляхом підстановки х_т = у_т рівняння (7.41) зводиться до рівняння

яке в теорії відомо як диференціальне рівняння, у загальному випадку нерозв'язне у квадратурах. Даним фактом і обумовлена неможливість побудови загальної динамічної теорії економічних флуктуацій. Можна затверджувати лише те, що в більшості випадків інтегральна крива рівняння (7.41) буде мати досить складну форму з наявністю локальних екстремумом, доводячи тим самим закономірний характер нерівномірності, динаміки макро- і мікропоказників.

Як уже вказувалося вище, модель (7.38) не враховує в явному виді можливі обмеження; вона містить екзогенний вектор {X}, що, однак, у реальності може включати аж ніяк не будь-які значення. Дійсно, постійні в часі прирості m — 1 благ (факторів) мають на увазі, що споживач (виробник) у відповідні моменти часу може придбати ці блага (фактори) у потрібній кількості. Однак якщо ці прирості занадто великі, те такої кількості благ (факторів) може не виявитися на товарному ринку (ринку ресурсів). Можливий випадок, коли необхідні закупівлі можуть бути зроблені лише з певним запізнюванням. He виключений також варіант, коли деякі товари (ресурси) застарівають (виснажуються) і взагалі зникають із ринку. B цьому випадку кожна споживча (виробнича) стратегія може бути отримана лише з деякою ненульовою ймовірністю, що рівносильні трансформації вихідної агрегатної функції корисності (виробничої функції) у функцію корисності Фон Неймана-Моргенштерна й розгляду динамічних способів виробництва. Такі побудови приводять рівняння (7.38) до стохастичного виду, у якому імовірнісні оцінки означають можливі порушення екзогенних траєкторій.

B даних моделях не розглядалися також наслідки ндогенні флуктуації в сферах виробництва й споживання. Однак і без детального аналізу ясно, що існування товарів, виробництво й споживання яких сильно осциюють, у тривалій перспективі не може не робити впливу на інші сегменти економіки. Такі збурювання, поширюючись по ринкових каналах зв'язку, будуть приводити до збою у виробництві й споживанні інших товарів, захоплюючи все більше їхнє число. B цьому змісті товари з осцилюючими характеристиками виробництва й споживання утворять усередині системи свого роду ядро динамічних флуктуацій, що постійно генерує внутрішні економічні шоки й тяжіє до детермінірованному самозростанню. Це, у свою чергу, веде до наростання в системі ентропії й збільшенню не стаціонарності й стохастичності її функціонування.

КОНТРОЛЬНІ ПИТАННЯ

1. Які припущення використаються в моделях економічних циклів Гудвина?

2. Опишіть зміни капіталовкладень і інших показників у різних варіантах моделі Гудвина.

3. B чим суть модифікацій моделей економічних циклів Гудвина?

4. Проведіть аналіз рішень моделей економічних циклів.

5. Якими факторами визначається динаміка корисності споживчих благ у зазначених моделях?

6. Ha яких економічних законах засновані ефекти, отримані в моделі динаміки корисності споживчих благ?

7. Яким образом ураховуються виробничі цикли в моделях динаміки корисності споживчих благ?

8. Як ураховується нестаціонарний випадок для даної моделі?

9. B чим сутність теореми про народження ендогенних флуктуацій у стаціонарно розширюється (стискальної) економіці?

10) Які висновки можна зробити по моделях?