Реброва М.П. Размытые множества в теории классификации // НТИ. Сер 2. – 1976. - № 10. – С. 15-21.

УДК 519.5.025.4.01

РАЗМЫТЫЕ МНОЖЕСТВА В ТЕОРИИ КЛАССИФИКАЦИИ

М. П. Реброва

I. Размытые множества

Решение многих информационных задач связано с разбиением множества каких-то определенных объектов на четко разграничиваемые классы, например, массив документов — на тематические подмассивы, множество запросов — на группы. Формальной предпосылкой по­становки таких задач служат «квазиопределения» [1] канторовской теории множеств, предполагающие, в час­тности, задание способа различения элементов множест­ва. В большинстве же реальных ситуаций возникает необходимость описывать переход элемента от одного множества к другому. Иллюстрацией того, каким обра­зом это можно сделать, служит введенное Л. Заде по­нятие размытого множества (в переводной литературе нечеткого, расплывчатого), интуитивно—класса, не име­ющего строго -определенных границ. Такое множество определяется путем задания степеней принадлежности каждого элемента множеству.

В связи с этим приведем ряд основных понятий тео­рии размытых множеств и размытых отношений [2,3].

Начнем с определений.

Определение 1. Размытое множество А в пространст­ве объектов Х — это множество упорядоченных пар {{х, /а (.»•))}, где !л(х) обозначает степень вхождения х в А, лежащую в интервале [0, I].

Носитель размытого множества А есть множество элементов х, для которых /а (х) положительна.

Ограничение области значения характеристической •функции вхождения единичным интервалом сделано в целях удобства. Принято считать, что чем ближе зна­чение функции к 1, тем выше степень вхождения объ­екта во множество. В этом случае, когда мы имеем дело с множеством в обычном смысле этого слова, его ха­рактеристическая функция вхождения принимает только два значения — 1 и 0, в зависимости от того, принад­лежит или нет объект множеству.

Пример 1. Пусть Х — множество действительных чи­сел, больших 1, а=|{о, 1, 5, 10, 100}. Тогда функция вхождения в размытое множество А может быть зада­на следующим образом:

/д(0)=0; /д(1)=0; /^(5) =0,01; /д (10) =0,2;

/^ (100) = 0,95.

Пример 2. Размытое множество А людей среднего воз­раста может быть задано таблицей его характеристи­ческой функции вхождения:

В этой таблице приведены те х, которые образуют носитель множества А.

Пример 3. Ранжирование объектов (терминов в час­тотных словарях, названий или кодов журналов при исследовании документальных потоков) можно рассмат­ривать как процедуру приписывания каждому объекту нормированной степени вхождения в размытое множест­во исследуемых объектов.

Примем для обозначения размытого множества вы­ражение

А^{(х.^(х))}.

В общем случае функция вхождения может быть задана различным образом: формулой, таблицей, неко­торым алгоритмом, либо через другие функции вхож­дения.

Понятие размытого множества не имеет статистичес­кой природы, поэтому схожесть характеристической функции вхождения ,с вероятностной, когда Х — пере­числимое множество, чисто внешнее. Особенно это ясно становится из последующих операций над размытыми множествами. (Вероятностная трактовка функций вхож­дения дана в '[4].)

Определение 2. Размытое множество А называется пустым (А=0), если характеристическая функция вхождения тождественно равна нулю (}л(х)=^0).

Определение 3. Размытое множество А совпадает с размытым множеством В (А=В}, если }л(х)=}в{х) для 'ух(^_х. В этом случае принято писать: /д-=/в.

Очевидно, что множества А и б имеют один и тот же носитель.

Определение 4. Дополнение размытого множества А обозначают А' и определяют через функцию вхождения следующим образом:

/Л——1-/А.

Определение 5. Размытое множество А называется подмножеством размытого множества В (АсгВ), если для всех х}л(х)<}в(х).

В этом и в дальнейших определениях носители мно­жеств А и В могут не совпадать, если, например, А-= •={(д:,, 0,6), (л:;, 0,3)} и В={(д-,, 0,8), (Хч, 0,5), (Хз.0,6)}, то Ас5.

Определение 6. Объединение двух размытых множеств А и В называется размытое множество С(С=А[)В), если /с=тах[/А, <в]. Последнее обозначается иногда так: ^с=!л\/^в. •

Определение 6'. Размытое множество С, являющееся объединением размытых множеств А и В (С==А\]В) с функцией вхождения ^с= спахал, ^в], называется наи-

Возраст х	40	41	42	43	44	45	46	47	48	49	50	51	52	53
Степень
вхождения {д (х)	0,3	0,5	0,8	0,9	1	1	1	1	1	0,9	0,8	0,7	0,5	0,3

ИНФОРМАЦИОННЫЙ АНАЛИЗ . НТИ . СЕР. 2 . № 10 . 1976 15

большим размытым множеством, содержащим как А, так и В.

Это определение связано с тем, что функция вхож­дения /с, ограниченная сверху /Е=1, имеет точную, верх­нюю границу. По аналогии с границами точечных мно­жеств (а каждое размытое множество можно рассмат­ривать, в свою очередь, как объединение составляющих его одноточечных множеств [5, с. 12]) объединение двух размытых множеств является наибольшим размытым множеством, содержащим А к В.

Определение 7. Пересечение двух размытых множеств А и В является размытым множеством С (С'=А(}В), если функция вхождения {с^ттЦл, /в], что обозна­чается /С=/АЛ/В.

Определение Т. Пересечением С двух размытых мно­жеств А и В называется наибольшее размытое множест­во, входящее одновременно в А и Д.

Это определение пересечения С связано с тем, что характеристическая функция вхождения ^е, ограниченная снизу }==0, имеет точную нижнюю границу.

Иллюстрация характеристической функции вхождения, соответствующей объединению двух размытых множеств (участки 1 и 2) и пересечению (участки 3 и 4), дана на рис. 1.

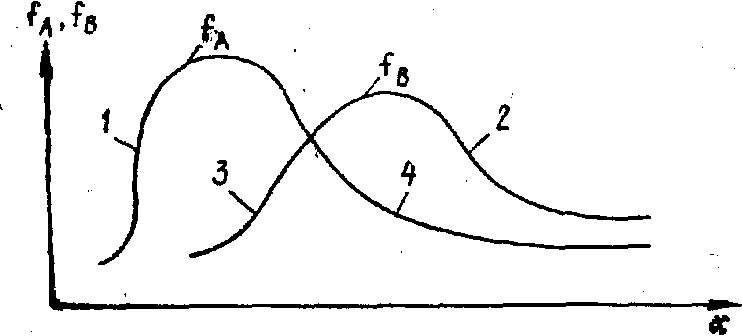
Рис. 1

Операции объединения, пересечения и дополнения над размытыми множествами удовлетворяют следующим •наиболее важным законам:

СП (А{]В}={С[}А) и (СГ}В)\ Дистрибутивные СЦ (апв) = (СЦА) П (СЦбЯ-законы

Ли(йиО=(^и5)иС) . ЛП (5ПО = (АПВ) ПС; Ассоциативные законы

(АиВ)'=А'Г\В'\ _ (А^Ву=А'^В'\ ^законы Моргана

Размытые множества в пространстве Х образуют дистрибутивную структуру с нулем и единицей [6, с. 16]. Роль нуля играет пустое множество, а единицы—все прОстранстьо X.

Алгебраические операции над размытыми множествами

Определение 8. Алгебраивческое произведение двух размытых множеств А я В обозвавается АВ и опреде­ляется а терминах функций вхождения соотношением /ав==/а/я. Понятно, что АВ<=А[\В.

Определение 9. Алгебраическая сумма двух размытых множеств А иВ обозначается через А+В к опреде­ляется /а+л=/а+/я, где /А+/да^1. Когда /д+/в>1, объект ве включается в алгебраическую 'сумму.

Операция, двойственная алгебраическому произведению, является прямой суммой АО)В=(А'В')'=А+В—АВ (теорема Ковера).

Для обычных множеств пересечение и алгебраическое произведение являются эквивалентными операциями, так же как Ц и ®. •

Определение 10. Абсолютная разность А и 5 обозна­чается /А—В/ и определяется через }л и /в следующим образом: //л-в/^Пл—Ы.

В случае обычных множеств множество /Л—В/ яв­ляется симметрической разностью А а В, определяемой:

/А-В{=(А\В)[}(В\А).

Выпуклость, ограниченность, отделимость размытых множеств в евклидовом пространстве

Соответствующие определения для обычных множеств» можло посмотреть ,в [7, с. 122, 123, 159].

Выпуклая комбинация. В основе многих важных раз­делов теории линейных пространств лежит понятие вы-' пуклости. В линейном пространстве Х множество назы­вается выпуклым, если оно вместе с любыми двумя точ­ками (х, у(:Х) содержит и соединяющий их отрезок. Под выпуклой комбинацией двух векторов / и § обычно» понимают линейную комбинацию / и §• в виде А^-г-' + (1—^)5, где О^Л^1.

Определение 11. Пусть А, В и Л—произвольные раз­мытые множества. Выпуклая комбинация обозначается через (А, В; Л) и определяется соотношением (А, В, Л) ^АА+А.'В. Пусть пространство Х является Евклидо­вым пространством размерности А. Обозначим его Е¹¹.

Определение 12. Размытое множество А в простран­стве Е¹¹ называется выпуклым, если множества" Га'='{^|/А(^)^а} выпуклые для всех а6[0,1]. (Мно­жества Га являются множествами в обычном смысле-слова—см. определение 9,части II.)

Приведем второе, равносильное первому, определение" выпуклости (доказательство см. в [2]).

Определение 12'. Размытое множество Л называется» выпуклым, если и[Кх1+(1-^,}хг]'^тт[}А(х1), Щх^)} для всех х\Хч^Х и Хб[0, I].

Второе определение никак не связано с выпуклостью-функции }{х), что видно из рис. 2. В обоих случаях

^м

' ^[^^Ц-Л1х,]

л, ^ х^ х; х

Я. х^{1-Л)х^ 1-ГлМ быпуклаго размытого мнажестКа И^х) нейыпутюго разттага множестЛа.

Рис. 2

знак 'выпуклости функции меняется, однако в первом' случае представлена функция выпуклого размытого^ мно­жества, а во втором — невыпуклого. Основное свойство-выпуклых размытых множеств состоит в том, что если-А и В выпуклые, то их пересечение также выпукло.

Ограниченность. Как. известно, для нормированных пространств понятие ограниченности совпадает с огра­ниченностью по норме, т. е. с возможностью поместить данное множество внутрь некоторого шара.

Определение 13. Размытое множество А ограничено в пространстве Е^, если множества Га={^|/А (х)^о^ ограничены для всех сб>0.

Возможны две интерпретации последнего опре­деления. Во-первых, для каждого а>0 сущест­вует множество /?('«) такое, что \\х\\<К{а} для всех -сбГа. Во-вторых, для каждого е>0 существует гиперплоскость Н такая, что {л(х)^е, для х, лежащих. по ту сторону от Я, которая не содержит начала коор­динат. Попробуем это показать. В линейном простран-