
- •Руководство для выполнения контрольной работы по эконометрике
- •Тема 1. Парная регрессия
- •1.1. Линейная парная регрессия
- •1.2. Нелинейная парная регрессия
- •1.2.4 Остаточная сумма квадратов отклонений:
- •1.2.6 Средняя относительная ошибка аппроксимации:
- •1.2.7 Средний коэффициент эластичности:
- •Тема 2. Множественная регрессия
- •Тема 3. Временные ряды
- •Распределение Дарбина-Уотсона
- •Литература
Тема 2. Множественная регрессия
Расчетные формулы.
2.1. Оценки вектора коэффициентов регрессии:
![]() .
.
2.2. Стандартизованные коэффициенты регрессии:
![]() .
.
2.3. Средние коэффициенты эластичности:
![]() .
.
2.4. Стандартная ошибка уравнения:
 .
.
2.5. Стандартная
ошибка параметра
![]() уравнения:
уравнения:
![]() ,
,
где
![]() диагональный элемент матрицы
диагональный элемент матрицы
![]() ,
находящийся на пересечении (
,
находящийся на пересечении (![]() )-й
строки и (
)-й
строки и (![]() )-го
столбца.
)-го
столбца.
2.6.
![]() статистики
параметров регрессии:
статистики
параметров регрессии:
![]() .
.
2.7. Парные коэффициенты корреляции:
![]() .
.
2.8. Множественный коэффициент корреляции:
![]() .
.
2.9. Множественный коэффициент детерминации:
![]() .
.
2.10. Скорректированный множественный коэффициент детерминации:
![]() .
.
2.11.
![]() критерий
Фишера:
критерий
Фишера:
![]() .
.
Если
![]() ,
где
,
где
![]() определяется
по уровню значимости
определяется
по уровню значимости
![]() и числу степеней свободы
и числу степеней свободы
![]() и
и
![]() ,
то уравнение регрессии значимо в целом.
,
то уравнение регрессии значимо в целом.
2.12. Частные
![]() критерии
для двухфакторной модели:
критерии
для двухфакторной модели:
![]() .
.
Если наблюдаемое
значение
![]() больше
больше
![]() ,
определяемого по заданному уровню
значимости
,
определяемого по заданному уровню
значимости
![]() и числу степеней свободы
и числу степеней свободы
![]() и
и
![]() ,
то дополнительное включение фактора
,
то дополнительное включение фактора
![]() в модель статистически оправдано. В
противном случае – нет.
в модель статистически оправдано. В
противном случае – нет.
Решение типовой задачи.
Имеются следующие
данные о сменной добыче угля на одного
рабочего
![]() (т), мощности угольного пласта
(т), мощности угольного пласта
![]() (м) и уровне механизации работ
(м) и уровне механизации работ
![]() (%),
характеризующие процесс добычи угля
на 10 шахтах:
(%),
характеризующие процесс добычи угля
на 10 шахтах:
Табл. 2.1
|
|
5 |
10 |
10 |
7 |
5 |
6 |
6 |
5 |
6 |
8 |
|
|
8 |
11 |
12 |
9 |
8 |
8 |
9 |
9 |
8 |
12 |
|
|
5 |
8 |
8 |
5 |
7 |
8 |
6 |
4 |
5 |
7 |
Требуется:
-
Полагая, что между переменными
 ,
,
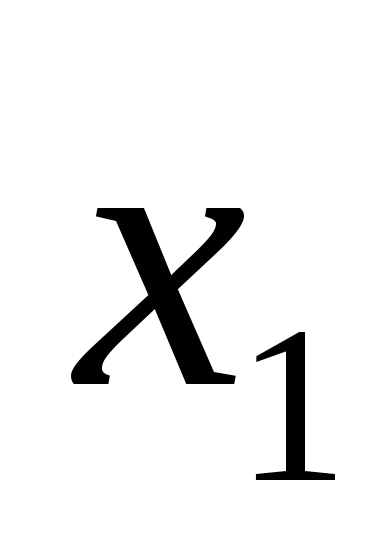 и
и
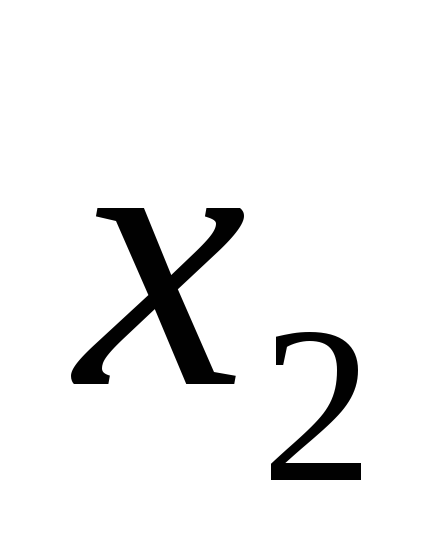 существует линейная корреляционная
зависимость, найти её аналитическое
выражение (уравнение регрессии). Пояснить
экономический смысл коэффициентов
регрессии.
существует линейная корреляционная
зависимость, найти её аналитическое
выражение (уравнение регрессии). Пояснить
экономический смысл коэффициентов
регрессии. -
Установить раздельное влияние на сменную добычу угля двух факторов через стандартизованные коэффициенты регрессии и средние коэффициенты эластичности.
-
Проверить значимость параметров множественной регрессии и при положительном ответе построить для коэффициентов уравнения регрессии 95% доверительные интервалы.
-
Сравнить значения скорректированного и нескорректированного коэффициентов множественной детерминации и проверить значимость полученного уравнения регрессии на уровне значимости
 .
. -
С помощью частных
 критериев
оценить целесообразность включения в
уравнение регрессии фактора
критериев
оценить целесообразность включения в
уравнение регрессии фактора
 после фактора
после фактора
 и наоборот – фактора
и наоборот – фактора
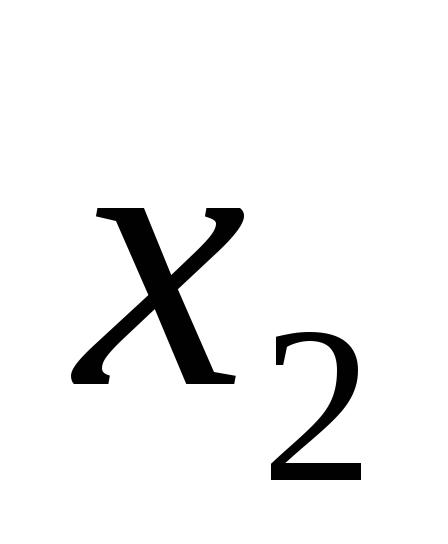 после
после
 .
.
Решение выполним в среде MS Excel.
-
Сформируем расчетную таблицу следующей структуры:
|
№ п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Сумма |
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднее |
|
|
|
|
|
|
|
|
|
|
|
|
Введем исходные
данные
![]() ,
,
![]() ,
,
![]() в таблицу по столбцам и рассчитаем
колонки
в таблицу по столбцам и рассчитаем
колонки
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,.
Вычисляем суммы и средние значения
столбцов с помощью встроенных функций
СУММ(…) и
СРЗНАЧ(…).
,.
Вычисляем суммы и средние значения
столбцов с помощью встроенных функций
СУММ(…) и
СРЗНАЧ(…).
Сформируем на свободном поле числовые матрицы:
 ,
,
 ,
,
где элементы матриц берутся из строки "Сумма" таблицы. Лучше задавать элементы матриц, используя знак "=" формулы Excel и щёлкая мышью по соответствующему элементу строки "Сумма", а затем - Enter.
Находим обратную
матрицу
![]() с использованием встроенной функции
МОБР(…).
Для этого выделяем на свободном поле
ячейки для элементов обратной матрицы
размером
с использованием встроенной функции
МОБР(…).
Для этого выделяем на свободном поле
ячейки для элементов обратной матрицы
размером
![]() .
При этом все ячейки, кроме левой верхней,
будут окрашены голубым цветом. В ней
набираем формулу: =МОБР(.: .), где в скобках
через двоеточие указываем крайние левый
и правый диагональные элементы матрицы
.
При этом все ячейки, кроме левой верхней,
будут окрашены голубым цветом. В ней
набираем формулу: =МОБР(.: .), где в скобках
через двоеточие указываем крайние левый
и правый диагональные элементы матрицы
![]() .
Далее нажимается клавиша F2
клавиатуры и затем одновременно
клавиши
"CTRL",
"SHIFT"
и "ENTER".
В указанных ячейках появятся элементы
искомой обратной матрицы.
.
Далее нажимается клавиша F2
клавиатуры и затем одновременно
клавиши
"CTRL",
"SHIFT"
и "ENTER".
В указанных ячейках появятся элементы
искомой обратной матрицы.
По формуле 2.1
находим вектор оценок
![]() с помощью встроенной функции МУМНОЖ(.;.).
Выделяем на свободном поле ячейки для
с помощью встроенной функции МУМНОЖ(.;.).
Выделяем на свободном поле ячейки для
![]() (это будет вектор размерности
(это будет вектор размерности
![]() ).
В строке
).
В строке
![]() или в первой ячейке указанного формата
набираем формулу =МУМНОЖ(…;…), где
вначале щелкаем по элементам обратной
матрицы, а затем через ";" – по
элементам вектора
или в первой ячейке указанного формата
набираем формулу =МУМНОЖ(…;…), где
вначале щелкаем по элементам обратной
матрицы, а затем через ";" – по
элементам вектора
![]() .
Снова нажимается клавиша F2
клавиатуры и затем одновременно
клавиши
"CTRL",
"SHIFT"
и "ENTER".
.
Снова нажимается клавиша F2
клавиатуры и затем одновременно
клавиши
"CTRL",
"SHIFT"
и "ENTER".
В итоге в отведенном формате имеем вектор оценок:
 .
.
Таким образом, уравнение регрессии в натуральном масштабе имеет вид:
![]() .
.
Из него следует,
что при увеличении угольного пласта на
1 м добыча угля на одного рабочего
увеличивается в среднем на 0,854 т, а
увеличение только уровня механизации
на 1% приводит к увеличению
![]() в среднем на 0,367 т.
в среднем на 0,367 т.
-
Найдем дисперсии и средние квадратические отклонения переменных:
![]()
![]() .
.
Вычислим стандартизованные коэффициенты регрессии по формуле 2.2:
![]() .
.
Уравнение регрессии в стандартизованном масштабе записывается:
![]() .
.
Оно показывает,
что с ростом фактора
![]() на одно
на одно
![]() при неизменности второго фактора рост
добычи угля на одного рабочего
увеличивается в среднем на 0,724
при неизменности второго фактора рост
добычи угля на одного рабочего
увеличивается в среднем на 0,724
![]() ,
а при увеличении только
,
а при увеличении только
![]() на одно
на одно
![]() результат
результат
![]() увеличивается в среднем на 0,284
увеличивается в среднем на 0,284![]() .
Отсюда видно, что первый фактор оказывает
большее воздействие на результат, чем
второй фактор.
.
Отсюда видно, что первый фактор оказывает
большее воздействие на результат, чем
второй фактор.
По формулам 2.3 определим средние коэффициенты эластичности:
![]() .
.
Таким образом,
увеличение по отдельности переменных
![]() ,
,
![]() на 1% приводит в среднем к росту результата
на 1% приводит в среднем к росту результата
![]() на 1,18% и 0,34% соответственно.
на 1,18% и 0,34% соответственно.
Из этого также
следует, что фактор
![]() оказывает большее влияние на
оказывает большее влияние на
![]() ,
нежели фактор
,
нежели фактор
![]() .
.
3. Вычислим
предсказанные моделью значения
![]() по формуле
по формуле
![]()
и тем самым заполним
колонку
![]() расчетной таблицы. Далее вычисляются
остатки
расчетной таблицы. Далее вычисляются
остатки
![]() и их квадраты
и их квадраты
![]() .
В итоге в строке "Сумма" колонки
.
В итоге в строке "Сумма" колонки
![]() таблицы определится остаточная сумма
квадратов
таблицы определится остаточная сумма
квадратов
![]() .
.
Находим стандартную ошибку уравнения регрессии по формуле 2.4:
![]() .
.
По формуле 2.5 вычисляем стандартные ошибки параметров уравнения:

С использованием
формулы 2.6 определяем
![]() статистики
параметров:
статистики
параметров:
![]() .
.
Найдем с помощью
функции СТЬЮДРАСПОБР(…)
табличное значение
![]() по уровню значимости
по уровню значимости
![]() и числу степеней свободы
и числу степеней свободы
![]() .
Сравнение модулей расчетных значений
с табличным указывает на статистическую
значимость параметра
.
Сравнение модулей расчетных значений
с табличным указывает на статистическую
значимость параметра
![]() . Параметры же
. Параметры же
![]() и
и
![]() не является значимым.
не является значимым.
Построим
интервальную оценку только для
коэффициента
![]() .
Для этого определим предельную ошибку,
которая в 95% случаев не будет превышена:
.
Для этого определим предельную ошибку,
которая в 95% случаев не будет превышена:
![]() .
.
Отсюда получаем искомый доверительный интервал:
![]() .
.
Из него следует,
что с надежностью 0,95 за счет увеличения
мощности пласта на 1 м переменная
![]() будет увеличиваться по разным шахтам
в пределах от 0,333 тонн до 1,375 т.
будет увеличиваться по разным шахтам
в пределах от 0,333 тонн до 1,375 т.
4. Вычислим парные коэффициенты корреляции по формулам 2.7:
![]() ;
;
![]() .
.
Определим множественный коэффициент корреляции по формуле 2.8:
![]() .
.
Множественный коэффициент корреляции достаточно высокий, что свидетельствует о существенной линейной зависимости результата от включенных в модель факторов.
Далее по формуле 2.9 находим множественный коэффициент детерминации:
![]() .
.
Таким образом, на
81% включенные в модель факторы определяют
воздействие на переменную
![]() ,
а на все остальные факторы, не включенные
в модель, приходится 19%.
,
а на все остальные факторы, не включенные
в модель, приходится 19%.
Скорректируем коэффициент детерминации по формуле 2.10:
![]() .
.
Рассчитаем дисперсионное отношение Фишера по формуле 2.11:
![]() .
.
Табличное значение
![]() =
=![]() определяем с помощью встроенной
статистической функции FРАСПОБР
по уровню значимости
определяем с помощью встроенной
статистической функции FРАСПОБР
по уровню значимости
![]() и числам свободы
и числам свободы
![]() и
и
![]() .
Поскольку
.
Поскольку
![]() ,
то можно сделать вывод о статистической
значимости построенной модели.
,
то можно сделать вывод о статистической
значимости построенной модели.
-
По формуле 2.12 находим частные
 критерии:
критерии:
![]() ,
,
![]() .
.
Табличное значение
![]() =5.59
определяем с помощью встроенной
статистической функции FРАСПОБР
по уровню значимости
=5.59
определяем с помощью встроенной
статистической функции FРАСПОБР
по уровню значимости
![]() и числам свободы
и числам свободы
![]() и
и
![]() .
Поскольку
.
Поскольку
![]() ,
то включение в модель фактора
,
то включение в модель фактора
![]() после
после
![]() оказалось статистически оправданным.
Но так как
оказалось статистически оправданным.
Но так как
![]() ,
то включение фактора
,
то включение фактора
![]() в модель после
в модель после
![]() оказывается бесполезным: влияние
оказывается бесполезным: влияние
![]() на переменную
на переменную
![]() не является устойчивым, систематическим
( в этом убедились ранее, признав
не является устойчивым, систематическим
( в этом убедились ранее, признав
![]() статистически незначимым).
статистически незначимым).
Отсюда вывод:
модель должна содержать только фактор
![]() .
.
Задания для самостоятельной работы.
Задача 2. Изучается влияние стоимости основных x1 и оборотных x2 средств на величину валового дохода y торговых предприятий. Для этого по 12 торговым предприятиям были получены данные, приведенные в таблице 2.2 (все величины измеряются в млн. руб.).
Табл. 2.2
|
Номер варианта |
Переменные |
Номер предприятия |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||
|
1 |
x1 |
3,9 |
4,8 |
3,9 |
4,3 |
4,8 |
4,9 |
5,6 |
4,6 |
5,6 |
7 |
7,2 |
7,7 |
|
x2 |
10 |
14 |
16 |
16 |
17 |
20 |
19 |
21 |
21 |
21 |
22 |
21 |
|
|
y |
7 |
8 |
7 |
7 |
7 |
8 |
9 |
8 |
9 |
11 |
11 |
11 |
|
|
2 |
x1 |
3,9 |
4,1 |
3,8 |
4,7 |
4,4 |
5,2 |
5,6 |
5,2 |
5,5 |
6,8 |
7,5 |
7,2 |
|
x2 |
10 |
14 |
15 |
16 |
18 |
19 |
19 |
20 |
21 |
21 |
22 |
21 |
|
|
y |
8 |
7 |
7 |
8 |
7 |
7 |
9 |
9 |
8 |
11 |
11 |
11 |
|
|
3 |
x1 |
4 |
4,3 |
4 |
4,9 |
4,4 |
4,9 |
6,3 |
4,8 |
6,2 |
7,7 |
7,6 |
7,1 |
|
x2 |
11 |
14 |
16 |
16 |
18 |
20 |
20 |
21 |
21 |
21 |
22 |
21 |
|
|
y |
7 |
7 |
7 |
7 |
7 |
8 |
8 |
8 |
9 |
11 |
11 |
11 |
|
|
4 |
x1 |
4,7 |
4,2 |
3,8 |
5 |
4,1 |
5,5 |
5,8 |
5 |
5,7 |
7,6 |
7,6 |
7,4 |
|
x2 |
11 |
14 |
16 |
17 |
17 |
20 |
20 |
21 |
20 |
20 |
21 |
22 |
|
|
y |
8 |
7 |
7 |
8 |
8 |
8 |
8 |
8 |
9 |
11 |
10 |
10 |
|
|
5 |
x1 |
4,4 |
4,4 |
4,2 |
4,2 |
4,1 |
5,1 |
5,7 |
4,8 |
5,6 |
7,6 |
7,7 |
7 |
|
x2 |
11 |
14 |
16 |
16 |
18 |
19 |
19 |
20 |
21 |
21 |
21 |
21 |
|
|
y |
7 |
7 |
8 |
8 |
8 |
8 |
9 |
9 |
8 |
10 |
10 |
11 |
|
|
6 |
x1 |
4,5 |
4,7 |
4,3 |
4,2 |
4,8 |
5,7 |
5,5 |
5,2 |
5,8 |
7,2 |
7,1 |
7,2 |
|
x2 |
10 |
15 |
16 |
16 |
18 |
20 |
19 |
20 |
21 |
20 |
21 |
22 |
|
|
y |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
10 |
11 |
10 |
|
|
7 |
x1 |
4,3 |
4,2 |
4,5 |
4,2 |
4 |
5,5 |
6,3 |
4,8 |
5,4 |
7,1 |
7,9 |
7 |
|
x2 |
11 |
15 |
15 |
16 |
17 |
19 |
20 |
21 |
21 |
20 |
22 |
22 |
|
|
y |
7 |
7 |
7 |
8 |
8 |
8 |
8 |
8 |
9 |
11 |
10 |
11 |
|
|
8 |
x1 |
4,1 |
4 |
4,2 |
5 |
4,6 |
5,1 |
6,2 |
4,9 |
6,2 |
7 |
7,5 |
7,4 |
|
x2 |
11 |
15 |
16 |
16 |
17 |
20 |
20 |
21 |
21 |
20 |
22 |
21 |
|
|
y |
7 |
7 |
7 |
7 |
7 |
7 |
8 |
9 |
8 |
10 |
10 |
11 |
|
|
9 |
x1 |
3,9 |
4,1 |
3,8 |
5 |
4,8 |
5,6 |
5,6 |
4,8 |
6 |
7,6 |
6,9 |
7,4 |
|
x2 |
11 |
14 |
15 |
16 |
18 |
20 |
20 |
21 |
21 |
20 |
22 |
21 |
|
|
y |
7 |
7 |
8 |
7 |
8 |
7 |
9 |
9 |
8 |
10 |
10 |
11 |
|
|
10 |
x1 |
4,9 |
4,2 |
4,6 |
4,2 |
3,8 |
4,9 |
5,4 |
5,3 |
5,4 |
7,4 |
7,6 |
6,9 |
|
x2 |
10 |
14 |
15 |
16 |
18 |
20 |
20 |
21 |
20 |
21 |
22 |
21 |
|
|
y |
7 |
7 |
8 |
7 |
8 |
8 |
8 |
8 |
8 |
10 |
10 |
11 |
|
Требуется:
1. Полагая, что между переменными y, x1, x2 существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии y по x1 и x2 ) и пояснить экономический смысл параметров регрессии.
2. Установить раздельное влияние на величину валового дохода двух факторов - основных и оборотных средств через стандартизованные коэффициенты регрессии и средние коэффициенты эластичности.
3. Проверить значимость коэффициентов регрессии и построить для них 95% доверительные интервалы.
4. Сравнить значения
скорректированного и не скорректированного
коэффициентов множественной детерминации
и проверить значимость полученного
уравнения регрессии по
![]() критерию
на уровне
критерию
на уровне
![]() =0,05.
=0,05.
5. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора x1 после x2 , и фактора x2 после x1.
